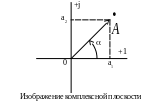- •1. Преимущества электрической энергии. Закон электромагнитной индукции.
- •1. Закон электромагнитной индукции
- •2. Электрическая цепь и ее элементы. Закон Ома. Законы Кирхгофа.
- •3. Закон полного тока. Закон Ома для магнитной цепи.
- •4. Получение синусоидальной э.Д.С. Синусоидальные величины, их мгновенные и амплитудные значения.
- •5. Действующие и средние значения синусоидальных величин
- •6. Изображение синусоидальных функций вращающимися векторами. Графики мгновенных значений. Векторные диаграммы.
- •7. Активная нагрузка в цепи переменного тока. Закон Ома. Временная и векторная диаграммы.
- •8. Индуктивная нагрузка в цепи переменного тока. Закон Ома. Временная и векторная диаграммы.
- •9. Емкостная нагрузка в цепи переменного тока. Закон Ома. Временная и векторная диаграммы.
- •4. Неразветвленная цепь переменного тока с r, l, c
- •11. Резонанс напряжений, условия резонанса и его признаки. Векторная диаграмма.
- •Резонанс в цепи с последовательно соединенными элементами (резонанс напряжений)
- •12. Разветвленная цепь однофазного тока. Треугольники токов и проводимостей.
- •13. Расчет разветвленной цепи переменного тока методом проводимостей.
- •14. Резонанс токов в простейшей разветвленной цепи. Условие и признаки. Векторная диаграмма.
- •15. Мощность однофазного тока. Треугольник мощностей. Коэффициент мощности и его значение.
- •16. Символический метод расчета цепей синусоидального тока. Сущность метода. Комплексы напряжения, тока, сопротивления и проводимости.
- •17. Законы Ома и Кирхгофа в символической форме.
- •18. Система трехфазного тока и ее преимущества. Получение трехфазного тока. Временная и векторная диаграммы э.Д.С. Представление векторной диаграммы на комплексной плоскости.
- •19. Соединение потребителей электроэнергии звездой с нейтральным проводом. Соотношение между фазными и линейными напряжениями и токами. Графическое определение тока в нейтральном проводе.
- •4. Симметричная нагрузка
- •20. Соединение потребителей электроэнергии звездой без нейтрального провода. Случай симметричной и несимметричной нагрузки. Векторные диаграммы. Напряжение смещения нейтрали.
- •21. Соединение потребителей электроэнергии треугольником. Соотношения между фазными и линейными напряжениями и токами. Случаи симметричной и несимметричной нагрузки.
- •22. Мощность трехфазного тока. Выражение для активной, реактивной и полной мощности при несимметричной и симметричной нагрузках.
- •23. Закон электромагнитной индукции. Устройство и принцип действия однофазного трансформатора.
- •24. Режим холостого хода трансформатора.
- •2. Опыт хх трансформатора
- •25. Работа однофазного трансформатора под нагрузкой. Уравнение для комплексов токов и уравнения равновесия напряжений для первичной и вторичной цепей.
- •Упрощенная схема замещения Трансформатора
- •27. Внешние хар-ки трансформатора, потери мощности и к.П.Д. Примеры применения трансформаторов на путевых и подъемно-транспортных машинах.
- •28. Принцип действия и устройство сварочного трансформатора. Внешние хар-ки трансформатора.
- •2. Сварочный трансформатор
- •2. Устройство асинхронного двигателя
- •31.Работа асинхронного двигателя под нагрузкой. Зависимости частоты, эдс и индуктивного сопротивления ротора от скольжения.
- •33.Энергетическая диаграмма и кпд асинхронного двигателя.
- •2. Энергетическая диаграмма ад
- •35.Вывод зависимости для электромагнитного вращающего момента ад. Анализ хар-к м(s) и n(м).
- •36.Рабочие хар-ки асинхронного двигателя, их анализ.
- •37.Способы пуска асинхронного двигателя с короткозамкнутым ротором.
- •1.Пуск асинхронного двигателя
- •38.Реверсирование асинхронного двигателя. Его сущность и принципиальная схема.
- •39.Способы регулирования частоты вращения асинхронного двигателя.
- •40.Торможение асинхронного двигателя. Анализ способа с помощью механических хар-к.
- •2. Торможение ад
- •41.Устройство и принцип действия 3-х фазного синхронного генератора. Холостой ход генератора.
- •2. Холостой Ход сг
- •42. Работа синхронного генератора под нагрузкой
- •43. Устройство машин постоянного тока.
- •44. Принцип действия генератора постоянного тока
- •Характеристика холостого хода синхронного генератора
- •47. Способы пуска электродвигателей постоянного тока. Пусковая диаграмма при реостатном пуске.
- •49.Реверсирование электродвигателей постоянного тока.
- •50. Способы торможения электродвигателя постоянного тока, анализ с помощью механических хар-к. Недостатки и достоинства..
- •51. Полупроводниковые приборы. Диоды.
- •Типы диодов[править | править исходный текст]
- •52. Транзисторы и тиристоры. Основные параметры.
- •Классификация транзисторов[править | править исходный текст]
- •По основному полупроводниковому материалу[править | править исходный текст]
- •По структуре[править | править исходный текст]
- •Устройство и основные виды тиристоров[править | править исходный текст]
- •53. Полупроводниковые выпрямители.
- •54 Однополупериодная система выпрямления однофазного тока.
- •55. Двухполупериодная мостовая система выпрямления однофазного тока.
- •56. Мостовая схема выпрямления трехфазного тока.
- •57. Понятие о сглаживающих фильтрах.
- •58. Определение и классификация Электропривода (эп).
- •59. Режимы работы эд
- •60. Расчет мощности эд в системе эп
- •61. Аппаратура управления Электроприводом
- •62. Пуск ад с кз ротором
14. Резонанс токов в простейшей разветвленной цепи. Условие и признаки. Векторная диаграмма.
Резонанс токов
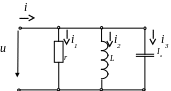
Рассмотрим следующую простейшую разветвленную цепь:
|
|
Пусть напряжение изменяется по синусоидальному закону (это действительно так).
Тогда полная проводимость равна:
![]()
![]() – Условие резонанса
токов.
– Условие резонанса
токов.
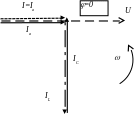
Векторная диаграмма при резонансе токов
В качестве исходного вектора удобно выбрать вектор напряжение.
|
|
Особенности резонанса токов
1) Полная проводимость всей цепи равна активной проводимости
![]()
2) ток в неразветвленной части цепи и приложенное к ней напряжение совпадают по фазе
![]()
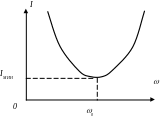
3) Ток в неразветвленной части цепи достигает минимальное значение
![]()
4) Ток в неразветвленной части цепи равен активному току
![]()
5) Токи в ветвях с индуктивностью и емкостью равны руг другу и противоположны по направлению. Эти токи могут значительно превышать ток в неразветвленной части цепи:
![]()
![]()
|
При резонансе токов
Мы рассмотрели идеальный случай. |
Если в ветвях с
индуктивностью и емкостью существуют
активные сопротивления
![]() и
и
![]() ,
то резонансная частота изменяется
,
то резонансная частота изменяется
![]()
Условие резонанса токов , как и прежде, но проводимости изменяются,
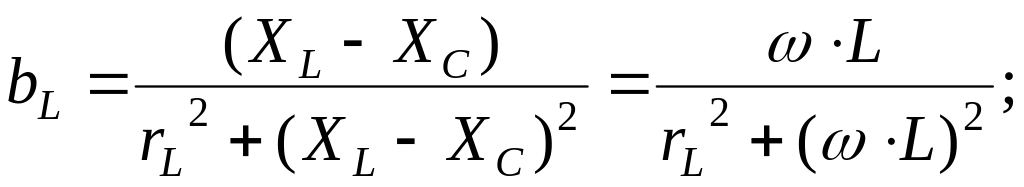
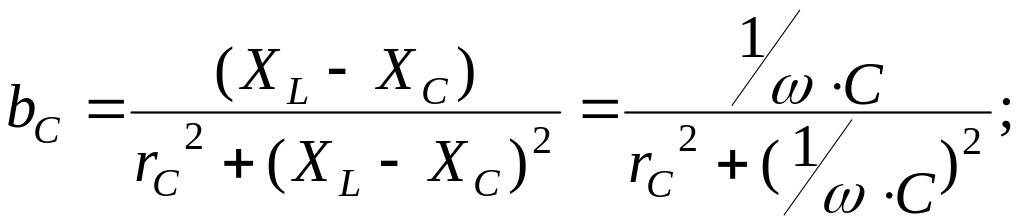
15. Мощность однофазного тока. Треугольник мощностей. Коэффициент мощности и его значение.
Мощность однофазного тока. Треугольники мощностей. Коэффициент мощности.
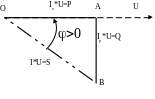
Если все стороны треугольника токов умножить на напряжение, получим треугольник мощностей:
|
– треугольник мощностей; Отсюда следуют важные соотношения:
|
В общем случае различают активную, реактивную и полную мощности однофазного тока:
![]() – активная мощность,
Вт;
– активная мощность,
Вт;
![]() – реактивная
мощность, ВАр;
– реактивная
мощность, ВАр;
![]() – полная мощность,
ВА;
– полная мощность,
ВА;
Из треугольника мощностей следует:
![]()
S
P=S*cos |
|
В ЭЛЕКТРОТЕХНИКЕ
![]() принято называть КОЭФФИЦИЕНТОМ МОЩНОСТИ.
принято называть КОЭФФИЦИЕНТОМ МОЩНОСТИ.
Источник электроэнергии должен выбираться на полную мощность, а в приемнике в полезную преобразуется только активная мощность. Поэтому повышение коэффициента мощности представляет собой важную задачей. Это повышение может быть осуществлено различными методами:
1) Подключением параллельно входным зажимам электропитания специальных конденсаторов;
2) Применением электромашинных синхронных компенсаторов;
3) Отключением электрооборудования, работающего в режиме Холостого Хода.
16. Символический метод расчета цепей синусоидального тока. Сущность метода. Комплексы напряжения, тока, сопротивления и проводимости.
Метод основан на использовании комплексных чисел (КЧ).
Существенное упрощение расчетов достигается путем замены вращающихся векторов, изображающих синусоидальные функции времени комплексными числами. В этом случае оказывается возможным распространить все методы расчета цепей постоянного тока на цепи переменного тока.
Поэтому дальнейшее ознакомление с к. ч. связано с введением в рассмотрение т. н. комплексной плоскости, где по оси абсцисс принято направлять ось действительных чисел, а по оси ординат – .
Символы +1 и +j на рис. 15 обозначают положительные направления вещественной и мнимой оси.
|
|
Вектор Комплексного Числа (КЧ)
![]() имеет две проекции
имеет две проекции
![]() и
и
![]() на вещественную и мнимую оси соответственно.
на вещественную и мнимую оси соответственно.
|
– алгебраическая форма записи КЧ;
|
|
– Модуль КЧ |
|
– аргумент КЧ |
|
|
Тригонометрическая форма записи КЧ |
|
Если воспользоваться формулой Эйлера , то получим показательную форму записи КЧ:
Показательная форма записи КЧ |
|
Сопряженными называются два таких КЧ, у которых действительные части одинаковые, а мнимые отличаются только знаком. Обозначаются со звездочкой наверху
|
|
Перейдем к электротехнике.
Вектора, изображающие синусоидальные функции времени, вращаются с угловой скоростью .
|
|
Поскольку все вектора вращаются с одинаковой скоростью, то относительно друг друга они неподвижны. Поэтому векторная диаграмма на комплексной плоскости строится для момента времени 0, и является неподвижной .
Комплексы напряжения, тока, сопротивления и проводимости.
Комплекс напряжения в показательной форме
Комплекс напряжения |
|
– модуль КЧ (действующее значение);
![]() – аргумент КЧ (начальная фаза).
– аргумент КЧ (начальная фаза).
Аналогично комплекс ЭДС в показательной форме
Комплекс ЭДС |
|
Комплекс тока |
|
Соответственно сопряженные значения обозначаются:
Сопряженные значения |
|