[Править]Криоскопическая и эбулиоскопическая константы

Коэффициенты пропорциональности К и Е в приведённых выше уравнениях — соответственно криоскопическая и эбулиоскопическая постоянные растворителя, имеющие физический смысл понижения температуры кристаллизации и повышения температуры кипения раствора с концентрацией 1 моль/кг. Для воды они равны 1.86 и 0.52 K·моль⁻¹·кг соответственно. Поскольку одномоляльный раствор не является бесконечно разбавленным, второй закон Рауля для него в общем случае не выполняется, и величины этих констант получают экстраполяцией зависимости из области малых концентраций до m = 1 моль/кг.

Для водных растворов в уравнениях второго закона Рауля моляльную концентрацию иногда заменяют молярной. В общем случае такая замена неправомерна, и для растворов, плотность которых отличается от 1 г/см³, может привести к существенным ошибкам.

Второй закон Рауля даёт возможность экспериментально определять молекулярные массы соединений, неспособных к диссоциации в данном растворителе; его можно использовать также для определения степени диссоциации электролитов.

[Править]Растворы электролитов

Законы Рауля не выполняются для растворов (даже бесконечно разбавленных), которые проводят электрический ток — растворов электролитов. Для учёта этих отклоненийВант-Гофф внёс в приведённые выше уравнения поправку — изотонический коэффициент i, неявно учитывающий диссоциацию молекул растворённого вещества:

;       

Неподчинение растворов электролитов законам Рауля и принципу Вант-Гоффа послужили отправной точкой для создания С. А. Аррениусом теории электролитической диссоциации.

Правило Вант-Гоффа — эмпирическое правило, позволяющее в первом приближении оценить влияние температуры на скорость химической реакции в небольшом температурном интервале (обычно от 0 °C до 100 °C). Я. Х. Вант-Гофф на основании множества экспериментов сформулировал следующее правило:

При повышении температуры на каждые 10 градусов константа скорости гомогенной элементарной реакции увеличивается в два — четыре раза.

Уравнение, которое описывает это правило следующее:

где   — скорость реакции при температуре  ,   — скорость реакции при температуре  ,   — температурный коэффициент реакции (если он равен 2, например, то скорость реакции будет увеличиваться в 2 раза при повышении температуры на 10 градусов).

Следует помнить, что правило Вант-Гоффа применимо только для реакций с энергией активации 60-120 кДж/моль в температурном диапазоне 10-400^oC. Правилу Вант-Гоффа также не подчиняются реакции, в которых принимают участие громоздкие молекулы, например белки в биологических системах. Температурную зависимость скорости реакции более корректно описывает уравнение Аррениуса.

Из уравнения Вант-Гоффа температурный коэффициент вычисляется по формуле:

Законы Рауля

Если упругость пара растворенного вещества очень мала P_B << P_A, то его парциальным давлением можно пренебречь (нелетучий компонент), и тогда упругость пара над раствором будет зависеть только от парциального давления растворителя: 

Это первый закон Рауля – парциальное давление над раствором прямо пропорционально мольной доле растворенного вещества. После подстановкиχ_A = 1 – χ_B и несложных преобразований 

получаем 

Относительное понижение упругости пара над раствором равно мольной доле растворенного вещества. Это закон Рауля для нелетучего растворенного компонента. Из этого закона можно вывести два следствия, которые в объединенном виде формируются как второй закон Рауля.

Рисунок 6.2 Зависимость повышения температуры кипения ΔTкип и понижения температуры замерзания  ΔTзам раствора от концентрации растворенного вещества.

На рис. 6.2 приведены зависимости P(T) чистого растворителя и двух его растворов P'(T) и P''(T).

Выразим мольную долю   через моляльную концентрацию   Для двухкомпонентного раствора  . При   << 1 получим 

Из подобия треугольников следует 

По определению, при   (B) = 1 моль∙  повышение температуры   равно   – эбулиоскопической константе для данного растворителя. Тогда повышение температуры кипения для данного раствора будет пропорционально его моляльной концентрации: 

Проведя аналогичное исследование, касающееся понижения температуры замерзания раствора, получим 

где K_кр – криоскопическая константа.

Второй закон Рауля – понижение температуры кипения и повышение температуры замерзания раствора прямо пропорционально моляльной концентрации раствора:

K_эб и K_кр являются экстраполяционными величинами от малых концентраций растворенного вещества, где выполняется этот закон, на C_m (B) = 1, где этот закон уже не действует (рис. 6.3). В табл. 6.2 приведены K_кр и K_эф для воды и бензола.

Рисунок 6.3 Иллюстрация справедливости второго закона Рауля для разбавленных растворов и экстраполяционной природы Kкр и Kэб

Kкр Kэб Вода 1,86 0,52 Бензол 5,07 2,60

Таблица 6.2 Криоскопические и эбулиоскопические константы для воды и бензола (град∙моль–1∙кг)

Второй закон Рауля дает легко осуществимую экспериментально возможность определения молекулярных масс некоторых молекулярных соединений, неспособных к диссоциации в данном растворителе. Действительно, моляльная концентрация растворенного вещества может быть представлена в виде соотношения C_m = g_B ∙ 1000 / μ_B ∙g_A, где g_A – вес растворителя, g_B – вес растворенного вещества, μ_B – его молярная масса. Тогда из ΔT = K_кр · m получим молярную массу растворенного вещества: 

20 вопрос

Теория растворов сильных электролитов

Теория сильных электролитов

Сильные электролиты полностью диссоциируют на ионы. В водных растворах сильных электролитов существуют простые или сольватированные катионы и анионы. Это подтверждается современными физическими и физико-химическими исследованиями. Однако опытным путем найдено, что электропроводность водных растворов сильных электролитов не эквивалентна той электропроводности, которую можно было бы ожидать при 100%-ной диссоциации молекул на ионы. Такое несоответствие объясняется теорией сильных электролитов, предложенной Дебаем и Хюккелем. Согласно этой теории, в растворах сильных электролитов между ионами существует электростатическое взаимодействие. Каждый ион окружен ионной атмосферой из противоионов. Ионная атмосфера тормозит движение ионов в электрическом поле, в результате чего создается эффект неполной диссоциации сильного электролита.

Мерой электростатического взаимодействия ионов является ионная сила раствора μ, равная полусумме произведений квадрата заряда каждого из присутствующих в растворе ионов на его концентрацию.

  

(1)

В связи с влиянием ионной силы раствора та концентрация, согласно которой ион действует в растворе, называется активной концентрацией (активностью):

                                                                 

,

(2)

где f – коэффициент активности, который характеризует взаимодействие ионов.

Коэффициент активности может быть рассчитан в зависимости от ионной силы по выражениям:

                                                 

при µ<10-2

(3)

                                    

при 10-2 < µ < 10-1

(4)

                       

+ 0,1z2µ при 0,1 < µ < 1

(5)

или взят из справочной литературы (необходимо объяснить учащимся, как пользоваться таблицей «Коэффициенты активности ионов при различной ионной силе»).

Активность необходимо использовать при расчете любого химического равновесия, если в системе находится сильный электролит, концентрация которого больше 1^.10^-4 моль/л.

РАСТВОРЫ ЭЛЕКТРОЛИТОВ, содержат в заметных концентрациях ионы-катионы и анионы, образующиеся в результатеэлектролитической диссоциации молекул растворенного в-ва. Р-ритель (чистый или смешанный) обычно в сколько-нибудь значит. степени не диссоциирован. Растворы электролитов обладают способностью проводить электрич. ток и относятся к проводникам второго рода. Благодаря увеличению общего числа частиц коллигативные св-ва бесконечно разбавленных растворов электролитов (т. е. св-ва, зависящие только от концентрации растворенного в-ва, но не от его природы) существенно отличаются от тех же св-в растворов неэлектролитов. Этим, в частности, объясняется увеличение осмотич. давления в сравнении со значением, предсказываемым законом Вант-Гоффа (см. Осмос), понижение давления пара р-рителя над р-ром в сравнении с предсказываемым Рауля законом и др. Наличиемионов обусловлены также классификация растворов электролитов, особенности теоретич. подходов в сравнении с др. классами р-ров. Наиб. изучены водные растворы электролитов, играющие важную роль во многих биол., геол. и техн. процессах. Неводные растворыэлектролитов служат средой для проведения синтеза и электрохим. процессов, используются в совр. технологиях (создание новыххимических источников тока, солнечных батарей, процессы разделения в-в и др.).

Классификация растворов электролитов основана на классификации электролитов. Соответственно о растворах электролитовговорят как о симметричных и несимметричных в зависимости от того, распадается ли молекула растворенного в-ва в р-ре на два ионаили на большее число частиц; z, z-зарядных [напр., р-р NaCl 1,1-зарядный, р-р СаС1₂ 2,1-зарядный] и т.п.-По степени диссоциацииэлектролита , к-рая равна отношению числа молекул, диссоциированных на ионы, к полному числу молекул в р-рс, различают сильные ( = 1), слабые ( << 1) электролиты и, соотв., р-ры сильных и слабых электролитов. Такое деление, однако, является условным и отражает состояние электролита в р-ре, определяемое не только природой растворенного в-ва и р-рителя, но и концентрацией(молярной долей х_эл), т-рой Т, давлением р.

В зависимости от состояния растворенного в-ва до растворения выделяют два класса растворов электролитов-р-ры ионофоров и р-ры ионогенов. Ионофоры в чистом состоянии существуют в виде ионных кристаллов (напр., галогениды щелочных металлов). В сильнополярных р-рителях (напр., в воде) ионофоры, как правило, диссоциируют полностью и составляют р-ры сильных электролитов. В слабополярных р-рителях (напр., в уксусной к-те) они образуют р-ры слабых электролитов. Ионогены до растворения состоят измолекул, они являются потенц. электролитами, электролитич. диссоциация проходит, как правило, в две стадии и обычно не полностью (хлорная к-та в уксусной к-те).

Растворители для растворов электролитов-как правило, полярные жидкости (чистые или смешанные). Чем больше диэлектрич. проницаемость  р-рителя, тем значительнее ослабляется сильное электростатич. притяжение противоположно заряженных ионов, что способствует возникновению в р-ре ионов. Интенсивное взаимод. последних с молекулами р-рителя приводит к связыванию ионов смолекулами р-рителя (см. Сольватация). Важна также способность молекул р-рителя выступать в качестве доноров или акцепторовпротонов или электронов. В зависимости от этих двух св-в различают четыре группы р-рителей: 1) протонные р-рители (вода, спирты, карбоновыс к-ты и др.), к-рые являются хорошими донорами протона и обладают высокой диэлектрич. проницаемостью ( > 15); 2) апротонные дшюлярные р-рители (нек-рые апротонные амиды, кстоны, сульфоксиды и др.), обладающие высокой диэлектрич. проницаемостью, но не обладающие донорно-акцепторными св-вами в отношении протона; 3) электронодонорные-р-рители (напр., эфиры); 4) неполяр-ныс р-рители (сероуглерод, углеводороды), к-рые обладают низкой диэлектрич. проницаемостью ( < 15) и не обладают донорно-акцепторными св-вами ни по отношению к протону, ни по отношению к электрону.

Находящиеся в растворах электролитов ионы могут существовать в виде своб. сольватир. ионов или в виде ассоциатов-контактных или сольватно разделенных ионных пар, тройников и т.д. Поскольку ионные пары не проводят электрич. ток, содержание своб. ионов врастворах электролитов определяется по его электрич. проводимости, в то время как общее число ионов (свободных и ассоциированных) можно определить, напр., спектрофотомет-рич. методами.

Термодинамика растворов электролитов. Равновесные термодинамич. св-ва растворов электролитов описываются парциальными молярными величинами, в к-рых различают катионные и анионные вклады. Напр., для электролита типа , состоящего из z₊-валентных катионов M^z+ и z_-валентных анионов X^-, хим. потенциал равен:

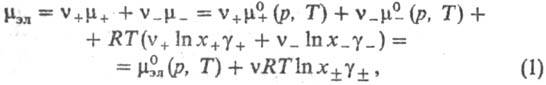
где v=v₊+v_, x₊ и х_--молярные доли катионов и анионов соотв., средняя молярная доля электролита х_b = = , ₊ и _ -коэффициенты активности катионов и анионов,  -средний коэф. активности электролита (см. Активность), и -стандартные хим. потенциалы катионов, анионов и электролита соотв., R-газовая постоянная.

Др. парциальные молярные величины связаны с _эл термо-динамич. соотношениями: парциальная молярная энтропия S_эл = -(9_эл/9Т)_p, парциальная молярная энтальпия H_эд_= = -Т²[(9_эл/Т)/9Т]_р, теплоемкость С_р = -Т(9²_эл/9Т²)_p, парциальный молярный объем V_эл = (9_эл/9р)_T.

В качестве стандартного состояния компонентов в растворах электролитов выбирают: для р-рителя-состояние чистой жидкости, для растворенного в-ва-состояние в гипотетич. р-ре, где его концентрация и активность равны единице, а термодинамич. св-ва , , равны соответствующим значениям для бесконечно разб. р-ра.

В электролитах с неполной степенью диссоциации (а < 1) выражение (1) заменяется соотношением:

где -средний ионный коэф. активности. Степень диссоциации а находят из условия хим. равновесия, к-рое в частном случае симметричного электролита (v+ =v_ = 1) приводит к ур-нию для константы диссоциации K_D (или константы ассоциации К_а):

где - коэф. активности недиссоциир. молекул (для разбавленных растворов электролитов  = 1). Аналогично (1) вводится также коэф. активности для р-рителя _S, к-рый связан с ионными коэф. активности Гиббса- Дюгема уравнением.

Для описания отклонения от идеального состояния разбавленных растворов электролитов используют кажущиеся осмотические коэффициенты, характеризующие отклонение осмотич. давления от значения, определяемого законом Вант-Гоффа, и связанные с ионными коэф. активности соотношением:

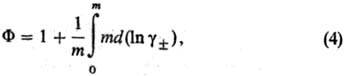
где m - моляльность электролита, _b-ионные коэф. активности в моляльной шкале, M_S-молярная масса (кг·моль^-1), x_S-молярная доля р-рителя.

Хим. потенциалы _эл, коэф. активности _b и осмотич. коэффициенты Ф м. б. определены экспериментально прямыми или косвенными методами: по давлению пара растворенного в-ва или р-рителя, по р-римости, по измерениям эдс электролитич. цепи. Из калориметрич. экспериментов находят парциальную молярную энтальпию H_эл, а из измерений плотности-парциальные молярные объемы V_эл. Поскольку измеримы только суммарные термодинамич. характеристики электролита, для катионов и анионов хим. потенциалы ₊ и _, их стандартные значения и , коэф. активности ₊ и _ и связанные с ними парциальные молярные величины м. б. определены только приближенно, на основе нетер-модинамич. допущений (напр., о равенстве вкладов одинаковых по размерам и степеням окислений катионов и анионов), путем экстраполяции эксперим. данных для различных растворов электролитов с общим катионом илианионом и др.

Наряду с хим. потенциалами ионов используют также электрохим. потенциал i-го иона с валентностью z_i:

где F-Фарадея постоянная, -внутр. электрич. потенциал раствора электролита (см. Межфазные скачки потенциала).

Статистические теории растворов электролитов основаны на методах стати-стич. механики, их осн. задача-расчет св-в исходя из энергии межчастичного взаимодействия. Развиваются след. подходы: ионный подход (уровень Макмиллана-Майера); ион-но-молекулярный подход (уровень Борна-Оппенгеймера); электрон-ядерный подход (уровень Шрёдингера). Ионный подход является традиционным и к настоящему времени наиб. развит. Он основан на рассмотрении в явном виде только ионов, р-ритель из явного рассмотрения исключается, что требует усреднения ф-ции распределения Гиббса по всем мол. конфигурациям р-рителя (см.Статистическая термодинамика). Энергия межионного взаимод. представляется как сумма слагаемых унарного, бинарного, тернарного и т.д. типов. Унарные слагаемые выражаются через своб. энергию сольватации W_i i-го иона, характеризуемую изменением энергии Гиббса системы при переносе иона из идеальной газовой фазы в бесконечно разб. р-р. Значение W_i совпадает с неидеальной частью стандартного хим. потенциала i-го иона, причем выделяют электростатич., неэлект-ростатич. и хим. вклады в значение W_i. Электростатич. вклад W_i^эл м. б. рассчитан согласно модели Борна, в рамках к-рой р-ритель рассматривается как бесструктурная среда, характеризуемая диэлектрич. проницаемостью :

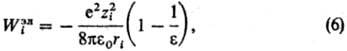
где ₀-диэлектрич. постоянная (диэлектрич. проницаемость вакуума), r_i-ионный радиус (см. Атомные радиусы). Для уточнения расчета вместо радиуса r_i используется эффективный радиус , где через _i учитываются размеры молекул р-рителя. Предпринимаются попытки моделирования р-рителя путем введения вместо  диэлектрич. ф-ции и учета нелинейных диэлектрич. эффектов.

К неэлектростатич. вкладам в W_i относят индукционный и дисперсионный вклады (см. Дисперсионное взаимодействие), а также вклад, связанный с работой, к-рую необходимо затратить для образования в р-рителе полости и внедрения в нее иона. Расчет этих вкладов производится теми же методами, что и для р-ров неэлектролитов. Для расчета энергии сольватации применяют квантовохим. методы.

Бинарные слагаемые в энергии межионного взаимод. выражаются через потенциалы W_ij(R), описывающие эффективное взаимод. ионовсортов i и j, находящихся на расстоянии R друг от друга. Соотв. тернарные слагаемые выражаются через потенциалы, описывающие трехчастичное взаимод. ионов и т. д. Учет бинарных и высших слагаемых в выражении для энергии межионного взаимод. позволяет описывать концентрац. зависимости термодинамич. св-в растворов электролитов.

Св-ва растворов электролитов характеризуются сложными концентрац. зависимостями, обусловленными конкуренцией вкладов разл. типов межчастичных взаимодействий. Обычно ограничиваются учетом потенциалов парного взаимодействия. Его существ. особенность-кулоновский характер межионного взаимод. на больших расстояниях (при : ,):

С кулоновским взаимод. связано экранирование межионных взаимод. и образование ионных комплексов, эти процессы характеризуются соотв. радиусом Дебая r_D =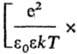 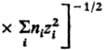 и радиусом Бьеррума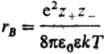 (k-пoстоянная Больцмана, n_i-плотностьионов i-го сорта). Первый из них (r_D) описывает расстояния, на к-рых экранируется поле иона за счет образования облака ионовпротивоположного знака, второй (r_B)-расстояния, на к-рых кулоновское притяжение между катионом и анионом превышает среднюю энергию теплового движения, что приводит к образованию ионных пар. Эффекты экранирования кулоновских взаимод. учитываются Дебая - Хюккеля теорией; в этой теории первое приближение определяет ионные коэф. активности в области предельных разбавлений (n_i : 0). Согласно теории Дебая - Хюккеля, коэф. активности ионов уменьшаются с концентрацией раствора электролита. Наличие врастворах электролитов ионных комплексов учитывается на основе представления о хим. равновесии между свободными и ассоциированными ионами, что приводит к ур-нию, аналогичному (3).

С увеличением концентрации электролита возникает необходимость учитывать и некулоновскую часть межионного взаимод., для чего прибегают к нек-рым моделям. При этом наряду с индукционным, дисперсионным, обменным и др. видами межчастичных взаимод. некулоновский потенциал учитывает сольватац. эффекты, связанные с влиянием р-ри-теля. В частности, учет некулоновской части взаимод. стабилизирует уменьшение коэф. активности ионов с концентрацией и может объяснить их увеличение, наблюдаемое экспериментально. Наипростейшей ионной моделью растворы электролитов является модель заряженных твердых сфер (т. наз. примитивная модель). Первые попытки описания примитивной модели были выполнены в рамках теории Дебая-Хюккеля (второе приближение). Более корректно учет размера ионов и неку-лоновского взаимод. осуществляется на основе методов статистич.термодинамики (см. Жидкость).

В рамках примитивной модели размеры ионов отличаются от кристаллографич. радиусов из-за сольватац. эффектов. Однако даже при одном и том же выборе размеров ионов удовлетворительно описать эксперим. результаты для разл. термодинамич. св-в растворахэлектролитов в примитивной модели оказалось затруднительным. К более корректным результатам приводит модель парного взаимод. типа "прямоугольной ямы", в к-рой ширина потенц. ямы выбирается равной диаметру молекулы р-рителя, а глубина ямы считается подгоночным параметром, учитывающим сольватац. эффекты; при этом используются кристаллографич. размеры ионов. В более реалистич. модели Фридмана в некулонов-ском потенциале межионного взаимод. выделяют три слагаемых, соответствующих: 1) главному отталкиванию ионов, определяемому их кристаллографич. размерами; 2) эффекту поляризации полости ионов р-рителем; 3) потенциалу Гер-ни-Франка, описывающему структурные эффекты, связанные с перекрыванием сольватных оболочек ионов при их сближении. Расчеты на основе ион-молекулярных моделей показывают, что на малых расстояниях межионные потенциалы имеют отталкивательный характер, на больших расстояниях, в соответствии с (7), зависят от расстояния между ионами асимптотически, как и при кулоновском взаимод., на промежут. расстояниях осциллируют вблизи этой асимптоты, причем с уменьшением размера иона (или с увеличением его валентности) амплитуда осцилляции возрастает, что соответствует усилению роли сольватац. эффектов.

Пренебрежение трехчастичными (и высшими) межионными взаимод. ограничивает возможности ионного подхода. В частности, для 1,1-зарядных водных растворов электролитов ионный подход обеспечивает количеств. описание термодинамич. св-в в областиконцентраций до 1 М. Учет концентрац. зависимости диэлектрич. проницаемости позволяет немного расширить эту концентрац. область. Формально расширения области применимости ионного подхода можно достигнуть, дополняя полученные с его помощью результаты разл. эмпирич. поправками. Примером такого подхода может служить полуэмпирич. ур-ние Питцера для осмотич. коэффициента или метод Робинсона-Стокса описания ионных коэф. активности с учетом гидратации (с помощью гидра-тац. чисел). Для описания многокомпонентных растворов электролитов широко используется правило Здановского, основанное на предположении о том, что смешение изописстич. р-ров разл. электролитов, химически не взаимодействующих между собой, происходит без измененияактивности р-рителя.

Ионно-молекулярный подход основан на рассмотрении в явном виде как ионов, так и молекул р-рителя. Главные результаты получены в 70-80-х гг. 20 в. на базе расчетных методов, интенсивно развиваемых в теории жидкостей. Это в осн. метод интегральных ур-ний для корреляц. ф-ций, метод кластерных разложений, теория возмущений, а также компьютерное моделирование. Благодаря явному учету ионно-молекулярных и межмолекулярных взаимод. возможно описание не только термодинамич., но и структурных св-в растворовэлектролитов. В частности, важный результат - описание сольватации ионов в зависимости от концентрации и др. параметров р-ра, объяснение концентрационных, температурных и барич. зависимостей св-в в широких интервалах состава, т-ры и давления.

Наипростейшей ион-молекулярной моделью растворов электролитов является ион-дипольная модель, в к-рой ионы рассматриваются как заряженные твердые сферы, а молекулы р-рителя моделируются твердыми сферами с дипольным моментом. Полученные выражения для термодинамич. ф-ций обобщают ур-ния, используемые в ионном подходе. В частности, в предельном случае малыхконцентраций выражения для ионных коэф. активности включают члены, основанные на теории Дебая-Хюккеля, а выражения для энергии сольватации-борновскую ф-лу (6) с эффективным радиусом иона , в к-ром поправка _i в явном виде зависит от диэлектрич. проницаемости р-рителя и соотношения размеров иона и молекулы. Выражение для диэлектрич. проницаемости удовлетворительно описывает эффект ее уменьшения при увеличении концентрации ионов.

Предпринимаются попытки учета квадрупольного элект-рич. момента и поляризуемости молекул р-рителя, а также взаимод., ответственных за образование в растворах электролитов ассоциатов и сольватов. Наиб. реальные модели разработаны в осн. для водных растворов электролитов и базируются обычно на компьютерном моделировании. Для описания ионно-молекулярных и межмолекулярных взаимод. применяют эмпирич. модели воды (модель ST2, модель центр. сил и др.), а также модели, основанные на квантовохим. расчетах. Рассчитанные парциальные радиальные ф-ции распределения дают информацию о структуре р-ра. В частности, с помощью ионно-молекулярных ф-ций определяют координац. числа сольватации. Найденные с помощью парциальных радиальных ф-ций структурные факторы удовлетворительно согласуются с данными дифракц. измерений.

Электрон-ядерный подход основан на учете электроста-тич. взаимод. между электронами и ядрами, входящими в состав ионов имолекул в растворах электролитов. Этот подход является наиб. последовательным, он основан на квантовомех. рассмотрении и разработан пока лишь для ион-молекулярных комплексов.

Важное значение в физ. химии растворов электролитов имеют исследования транспортных св-в, особенно электрич. проводимости (см.Электропроводность электролитов). Наличие ионов заметно сказывается на диффузии, вязкости, теплопроводности.

Ионная сила раствора — мера интенсивности электрического поля, создаваемого ионами в растворе. Полусумма произведений из концентрации всех ионов в растворе на квадрат их заряда. Формула впервые была выведена Льюисом:

,

где c_B — молярные концентрации отдельных ионов (моль/л), z_B заряды ионов

Суммирование проводится по всем типам ионов, присутствующих в растворе. Если в растворе присутствуют два или несколько электролитов, то вычисляется общая суммарная ионная сила раствора.

Например, для раствора NaCl с концентрацией 0,001 моль/л, в котором присутствуют два вида однозарядных ионов Na⁺ и Cl⁻ с концентрациями также равными 0,001 моль/л, ионная сила будет вычисляться следующим образом:

I(NaCl) = 0,5(z²(Na⁺)•c(Na⁺) + z²(Cl⁻)•c(Cl⁻)) = 0,5(1²•c(NaCl) + (-1)²•c(NaCl)) = c(NaCl)

И ионная сила соответственно будет равна концентрации раствора:

I = 0.5(1²•0,001 моль/л + (-1)²•0,001 моль/л) = 0.5(0,001 моль/л + 0,001 моль/л) = 0,001 моль/л

Это верно для раствора любого сильного электролита, состоящего из однозарядных ионов. Для электролитов, в которых присутствуют многозарядные ионы, ионная сила обычно превышает молярность раствора.

Ионная сила раствора имеет большое значение в теории сильных электролитов Дебая — Хюккеля. Основное уравнение этой теории (предельный закон Дебая — Хюккеля) показывает связь между коэффициентом активности иона ze и ионной силы раствора I в виде:

,

где γ — коэффициент активности, А — постоянная, не зависящая от заряда иона и ионной силы раствора, но зависящая от диэлектрической постоянной растворителя и температуры.

Активность компонентов раствора — эффективная (кажущаяся) концентрация компонентов с учетом различных взаимодействий между ними в растворе, то есть с учетом отклонения поведения системы от модели идеального раствора.

Содержание   [убрать]  1 Выбор стандартного состояния 2 Методы определения активности 2.1 По равновесному давлению пара 2.2 По повышению температуры кипения раствора 2.3 По понижению температуры замерзания раствора 2.4 По осмотическому давлению раствора 2.5 По распределению компонента между конденсированными фазами 2.6 По равновесию химической реакции с газовой фазой 2.7 По значению э. д. с. гальванического элемента 3 Литература 4 Ссылки

Активность была предложена в 1907 году Льюисом как новая переменная, применение которой вместо концентрации позволяет использовать для описания свойств реальных растворов относительно простые уравнения, полученные для идеальных систем. Альтернативой этому пути является использование более сложных уравнений, учитывающих взаимодействие между частицами (см., например, уравнение Ван-дер-Ваальса).

Активность отличается от общей концентрации на некоторую величину. Отношение активности ( ) к общей концентрации вещества в растворе называется коэффициентом активности:

Коэффициент активности служит мерой отклонения поведения раствора (или компонента раствора) от идеального. Отклонения от идеальности могут быть обусловлены различными химическими и физическими причинами — дипольные взаимодействия, поляризация, образование водородных связей, ассоциация, диссоциация, сольватация и др.^[1]

Исходя из понятия химического потенциала, активность компонента в растворе можно определить как величину, которую нужно подставить в выражения для химического потенциала компонента в идеальном растворе:

(где   — химический потенциал чистого  -го компонента) вместо мольной доли x, для того, чтобы получить действительное значение химического потенциала  -го компонента в реальном растворе:

где   — стандартный химический потенциал.^[2]

Размерность и величина активности зависит от используемого способа выражения концентрации — если   (активность при выражении концентрации как мольной доли) величина безразмерная, то   и   (для молярности и моляльности соответственно) — размерные величины, выражаются в моль/л и моль/кг.

Коэффициент активности в общем случае может быть как больше, так и меньше единицы (при этом говорят о положительных или отрицательных отклонениях от идеального поведения соответственно, или о положительных и отрицательных отклонениях от закона Рауля). Возможны и знакопеременные отклонения от идеального поведения (то есть коэффициент активности меньше единицы при одних концентрациях, и больше — при других). Так, например, для железа в системе Fe-S при 1300 °C в^[3] рекомендуются коэффициенты активности от 0,004 при   до 1,47 при  .

Отметим, что величина активности и коэффициента активности может быть различной в зависимости от выбора стандартного состояния.