Потрійний інтеграл

Потрійний інтеграл є безпосереднім узагальненням подвійного інтеграла на тривимірний простір. Теорія потрійного інтеграла аналогічна теорії подвійного інтеграла, тому в більшості випадків ми обмежимося лише формулюваннями тверджень і короткими поясненнями.

Означення. Якщо інтегральна сума (31) при    має скінченну границю   , яка не залежить ні від способу розбиття області    на частини   , ні від вибору в них точок   , то ця границя називається потрійним інтегралом від функції   по області    і позначається одним із таких символів:

                             або  

Таким чином, за означенням

                              

де  функція   називається інтегровною в області  ,     область інтегрування,     змінні інтегрування,   (або   )   елемент об’єму.

Теорема (достатня умова інтегровності функції). Якщо функція   неперервна в замкненій обмеженій області  , то вона в цій області інтегровна.

Геометричний зміст потрійного інтеграла. Якщо  ,  , то потрійний інтеграл дорівнює об’єму   тіла  :

                                                                                                    (32)

Якщо по тілу   розподілено масу з об’ємною густиною   у точці  , то маса   цього тіла знаходиться за формулою:

                                                                                     (33)

Оскільки довільну функцію    можна тлумачити як густину деякого розподілу маси, то формула (33) дає нам механічний зміст потрійного інтеграла.

Механічний зміст потрійного інтеграла. Якщо  , то

                                             

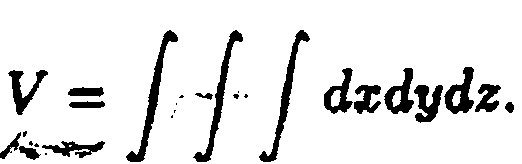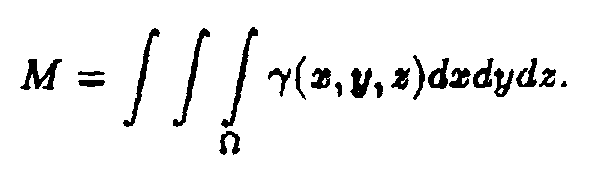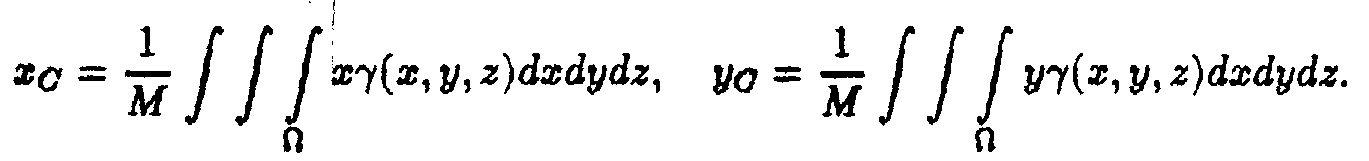
Застосування потрійного інтеграла  1°. Об'єм тіла, що займає область Ω Ω 2°. Маса (тіла, що займав область   з змінною густиною  визначається потрійним інтегралом і/ j \ 3°. Координати центра ваги тіла, яке займає область обчислюються за формулами 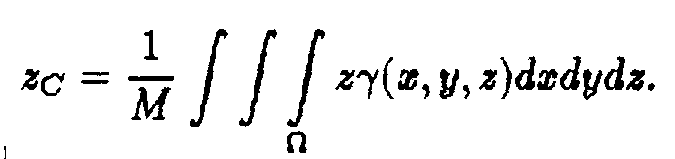4°. Моменти інерції (геометричні, тобто ) відносно осей координат відповідно становлять:

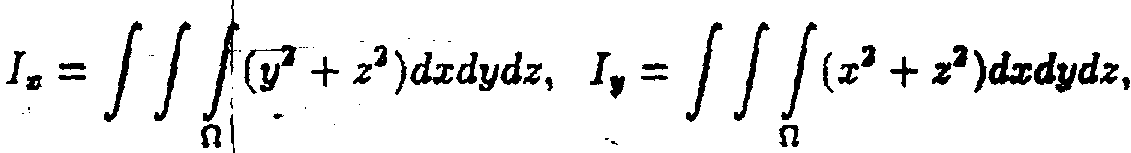
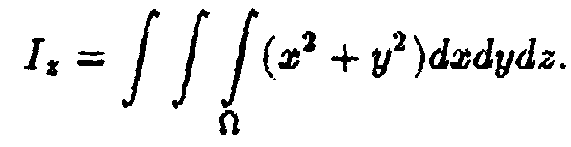
Властивість 1 (однорідність потрійного інтеграла). Сталий множник можна винести за знак потрійного інтеграла:

                           

Властивість 2. Потрійний інтеграл від алгебраїчної суми скінченної кількості інтегровних в області   функцій дорівнює алгебраїчній сумі потрійних інтегралів від цих функцій:

                  

Властивість 3. Якщо в області   функція  , то

                                                 

Властивість 4 (інтегрування нерівності). Якщо   у довільній точці  , то

                                      

Властивість 5 (адитивність по області інтегрування). Якщо область інтегрування   функції   є об’єднанням областей  , що не мають спільних внутрішніх точок, то

                   

Властивість 6 (оцінка потрійного інтеграла). Якщо функція   неперервна в замкненій обмеженій області  , яка має об’єм  , то

                                          

де   і     відповідно найменше і найбільше значення функції   в області  .

Властивість 7 (теорема про середнє значення). Якщо функція   неперервна в замкненій обмеженій області  , яка має об’єм  , то в цій області існує така точка  , що

                                       

Величину     називають середнім значенням функції   в області  .

Подвійний інтеграл

Означення. Якщо інтегральна сума (5) при   має скінченну границю  , яка не залежить ні від способу розбиття області   на частинні області  , ні від вибору точок   в них, то ця границя називається подвійним інтегралом від функції   по області   і позначається одним із символів:

                                    або   

Таким чином, за означенням

                                                               (6)

У цьому випадку функція   називається інтегровною в області  ,     областю інтегрування,   і     змінними інтегрування,   (або   )   елементом площі.

 

 

Теорема (достатня умова інтегровності функції). Якщо функція   неперервна в замкненій обмеженій області  , то вона інтегровна в цій області.

                                              (7)

                                                                                             (8)

Формула (7) дає нам геометричний зміст подвійного інтеграла.

Геометричний зміст подвійного інтеграла. Якщо  , то

                                                 

Механічний зміст подвійного інтеграла. Якщо  , то

                                                 

де     маса пластинки з густиною   в точці  .

Властивість 1 (однорідність подвійного інтеграла). Сталий множник можна винести за знак подвійного інтеграла:

                              

Властивість 2. Подвійний інтеграл від алгебраїчної суми скінченної кількості інтегровних в області   функцій дорівнює алгебраїчній сумі подвійних інтегралів від цих функцій:

                     

Властивість 3. Якщо в області   функція  , то

                                                  

Властивість 4 (інтегрування нерівності). Якщо   у довільній точці  , то

                                        

Властивість 5 (адитивність по області інтегрування). Якщо область інтегрування   функції   є об’єднанням областей  , що не мають спільних внутрішніх точок, то

           

Властивість 6 (оцінка подвійного інтеграла). Якщо функція   неперервна в замкненій обмеженій області  , яка має площу  , то

                                            

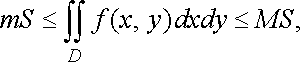
де   і     відповідно найменше і найбільше значення підінтегральної функції в області  .

Властивість 7 (теорема про середнє значення). Якщо функція   неперервна в замкненій обмеженій області  , яка має площу  , то в цій області існує така точка  , що

                                           

Величину

                                          

називають середнім значенням функції   в області  .

Теорема. Якщо перетворення (14) переводить замкнену обмежену область    в замкнену обмежену область    і є взаємно однозначним, і якщо функції (14) мають в області    неперервні частинні похідні першого порядку і відмінний від нуля визначник

                                                                                            (16)

а функція   неперервна в області   , то справедлива така формула заміни змінних:

                                        (17)

Криволінійний інтеграл

Означення. Якщо інтегральна сума (48) при    має скінченну

границю   , яка не залежить ні від розбиття кривої   , ні від вибору точок   , то цю границю називають криволінійним інтегралом першого роду (або криволінійним інтегралом по довжині дуги) від функції    по кривій    і позначають   .

Таким чином, за означенням

                                                                        (49)

Якщо границя (49) існує, то функція   називається інтегровною на кривій  , крива     контуром інтегрування,     початковою, а     кінцевою точками інтегрування.

Криволінійний інтеграл першого роду зводиться до визначеного інтеграла за формулою:

                                           

Геометричний зміст криволінійного інтеграла першого роду. Якщо визначений інтеграл   при   представляє собою площу криволінійної трапеції , то криволінійний інтеграл   при

 чисельно дорівнює площі частини циліндричної поверхні, твірні якої мають довжину   і паралельні осі  , а напрямна збігається з кривою   на площині   

Фізичний зміст криволінійного інтеграла першого роду. Якщо крива     матеріальна, тобто вздовж кривої розподілено з лінійною густиною   деяку масу  , то

                                    

тобто з фізичної точки зору криволінійний інтеграл першого роду від невід’ємної функції вздовж деякої кривої дорівнює масі цієї кривої.

Властивості

Площа циліндричної поверхні. Площа   циліндричної поверхні, визначеної функцією  , обчислюється за формулою:

                                                                                                (56)

Довжина кривої. Довжина   кривої   визначається за формулою:

                                                                   

Маса кривої. Маса кривої   обчислюється за формулою:

                                                                                                  (58)

Центр маси та статичні моменти кривої. Координати   центра маси кривої   обчислюються за формулами:

                                              (59)

де     статичні моменти кривої   відносно осей  .

Моменти інерції кривої. Моменти інерції   кривої   відносно осей   і початку координат відповідно дорівнюють:

                                                   

Криволійнійний інтеграл 2-го роду

Означення. Якщо інтегральна сума (62) при    має скінченну границю   , яка не залежить ні від розбиття кривої   , ні від вибору точок   , то цю границю називають криволінійним інтегралом від функції    (    ) по координаті    (    ) вздовж кривої    і позначають   .

Таким чином,

                                    

Суму

                                           

називають криволінійним інтегралом по координатах або криволінійним інтегралом другого роду від функцій   і   по кривій   і позначають символом

                                             

Теорема (Гріна). Нехай     деяка правильна область, обмежена замкненим контуром   , і функції   неперервні разом із своїми частинними похідними    у цій області. Тоді справедлива формула Гріна

                                          

Площа плоскої фігури. Одне із застосувань формули Гріна полягає в тому, що вона дозволяє обчислювати площу області з кусково-гладкою межею за допомогою криволінійного інтеграла. Так, якщо у формулу (72) підставляти  , а потім підставляти  , то дістанемо, що площу обмеженої плоскої області   з кусково-гладкою межею   можна обчислити за довільною з формул

                                       

Означення числового ряду, його збіжності. Геометрична прогресія та гармонічний ряд

Нехай задана нескінченна послідовність чисел  Нескінченна сума чисел виду  - називаєтьсячисловим рядом, а числа  - членами ряду.

Ряд позначають так:

Вираз для  - го члена ряду при довільному натуральному  > , називається загальним членом ряду і позначається  .

Загальний член ряду можна задати формулою  , з допомогою якої записується довільний член ряду.

Суму   перших його членів позначають через :

і прийнято називати  -ою частинною сумою ряду.

Часткові суми ряду утворюють деяку числову послідовність його часткових сум  . Ряд називається збіжним, якщо збігається послідовність його часткових сум  , тобто якщо існує скінчена границя

Число   при цьому називають сумою ряду і записують

При цьому вважають також, що ряд збігається до числа  .

Якщо послідовність часткових сум ряду розбігається, то ряд називається розбіжним. У цьому випадку ряд не має суми.

Ряд, що складений з елементів геометричної прогресії називаєтьсягеометричним рядом:

Число   — знаменник геометричної прогресії.

Позначимо   сума   перших членів прогресії та знайдемо її значення:

Звідси отримуємо

Якщо  , то

геометричний ряд збігається.

Якщо  , то

Якщо  , то

Якщо  , то

таким чином, послідовність   - розбіжна.

Ряд вигляду

називається гармонічним рядом. Він розбіжний.

Числовий ряд вигляду

називається узагальненим гармонічним рядом. Доведено, що при   узагальнений гармонічний ряд розбігається, а при   -ряд збігається.

Якщо ряд збігається, то різниця між сумою   і частинною сумою його 

називається   -им залишком ряду.

Залишок   ряду являє собою ту похибку, яка одержиться, якщо замість наближеного значення суми ряду  взяти суму перших   членів цього ряду. Але оскільки   є границя суми  , то для збіжного ряду виконується

Таким чином, взявши достатньо велике число членів збіжного ряду, можна суму цього ряду обчислити з любою точністю. Звідси випливає, що основною задачею теорії рядів є дослідження збіжності ряду.

Знакозмінні та знакопочергові числові ряди. Ознака збіжності Лейбніца

Окрім знакододатних рядів на практиці зустрічаються знакозмінні та знакопочергові ряди. Про них і піде мова в даній статті.

Ряд

називається знакозмінним, якщо частина його членів приймає додатні значення, а решта - від'ємні.

Знакопочерговим називається ряд, сусідні члени якого мають протилежні знаки. У випадку, коли перший член знакопочергового ряду додатний, його можна подити у вигляді

Для дослідження збіжності ряду використовують ознаку Лейбніца: якщо члени знакопочергового ряду спадають по абсолютній величині та

то ряд збіжний. При цьому сума ряду не перевищує значення його першого члена, якщо він додатній.

Для знакозмінного ряду існують поняття абсолютної та відносної збіжності.

Знакозмінний (знакопочережний) ряд збіжний абсолютно, якщо цей ряд та ряд утворений з модулів членів цього ряду збіжні одночасно. Ряд називають умовно або неабсолютно збіжним у випадках, коли збіжний лише знакозмінний ряд, а ряд складений з абсолютних величин членів ряду розбігається.