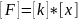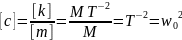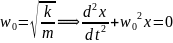12. Второй закон Ньютона.
Ответ:
Импульсом тела (количеством движения) называется векторная величина
.
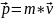Формулировка Ньютона: Производная импульса по времени равна результирующей силе.
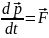(1)
Частный случай: предположим, что масса тела неизменна – что часто бывает.
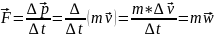(2)
2-ой закон Ньютона в форме (2) и даже (1) не работает для релятивистских скоростей, когда скорость частицы приближена к скорости света.
2-ой закон Ньютона в форме (2) и даже (1) с тем смыслом силы F, который мы в них вкладываем, не работает в НСО.
Пример: поезд тормозит, человек с верхней полки падает.
2-ой закон Ньютона в форме (2) не работает если масса непостоянна.
13. Третий закон Ньютона.
F12
F21
m2
m1
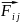– сила, с которой
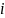-тое
тело действует на
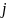-тое
тело.
Между
силам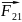и
и
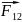существует связь:
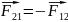
Ньютон назвал одну из сил действием, а другую – противодействием.
Третий закон Ньютона: Сила действия равна и противоположно направлена силе противодействия.
Вытекает ли из 3-его закона Ньютона равновесие тел? – Никакого равновесия тел не будет, потому что равновесие возможно, когда векторная сумма всех сил, приложенных к телу равна нулю, а здесь же силы приложены к разным телам.
14. Законы изменения и сохранения кинетической энергии – случай одномерного движения.
Ответ: (лекция судебников, была в группе, попыталась хоть как-то разобраться – получилось не особо)
Рассмотрим
материальную точку. Так как движение
одномерно, то МТ имеет только одну
проекцию скорости движения
./
/
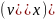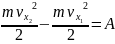– искомый закон изменения кинетической
энергии материальной точки: изменение
кинетической энергии материальной
точки при её движении из х1 в х2
= работе силы, действующей на материальную
точку.
Полагая, что Fx = 0, тогда A = 0 и
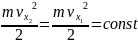
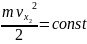
15. Законы изменения и сохранения кинетической энергии – общий случай криволинейного движения.
Ответ: (не проходили, инфа была в следующей лекции за той, что лежала в группе, то есть ответ не сфотографирован был, поэтому где искать ответ – понятия не имею, ибо в инете не нашла)
16. Механические гармонические колебания – вывод дифференциального уравнения движения пружинного маятника.
Ответ:
Система, состоящая из тела массой m, скользящего по идеально гладкой плоскости, прикрепленного пружиной жесткости k к вертикальной стенке, называется пружинным маятником.
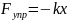– сила направлена противоположно
смещению.
Коэффициент пропорциональности k – коэффициент жесткости.
Вывод дифференциального уравнения движения пружинного маятника:
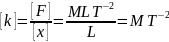
Составим уравнение движения для частицы:
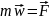
Проецируем на ось x:
,
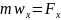
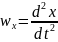где х – координата перемещения.Подставляем:
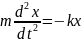
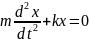
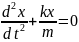
Введем
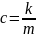
Полученное уравнение называется дифференциальным уравнением пружинного маятника.
Дифференциальным уравнением называется уравнение, в котором неизвестная функция входит под знаком дифференцирования.
Поскольку производная 2-ого порядка, то и уравнение называется дифференциальным уравнением 2-ого порядка.
17. Механические гармонические колебания – решение дифференциального уравнения движения пружинного маятника.
Ответ: (взаимосвязан с предыдущим вопросом)
Решением уравнения является функция (в общем виде) или число (в частном случае), которое, будучи подставленным в это уравнение, превращает его в верное тождество для любого момента времени.
В конкретном случае мы должны найти такую «чудесную» функцию, которая, если два раза продифференцировать, возвращается в исходное состояние с противоположным знаком.
Такой функцией является либо sin(), либо cos().
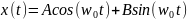, где А, В = const.
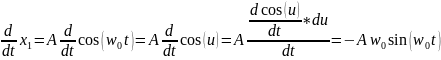
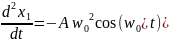
Мы доказали, что функция является решением дифференциального уравнения, полученного нами ранее.
Для выяснения вида решения сделаем следующее предположение: пусть в момент времени t = 0 мы отклонили маятник на x0 и отпустили без начальной скорости.
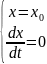– начальные условия при t
= 0.
Посмотрим, какое решение будет в этом случае:
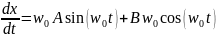
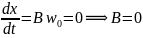(При t = 0).
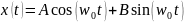
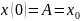
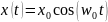
Вывод: данное тело, названное нами пружинным маятником, совершает гармонические колебания с периодом Т.
Гармонические колебания – колебания, описывающиеся «гармонической» функцией cos().
Колебания – повторяющиеся движения.
Периодическая функция – функция f(t) является периодической, если существует некоторое Т, такое, что для любого t верно f(t+T)=f(t).
Т – период.