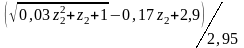Для улучшенных сталей

m = 6;

для закалённых сталей

m = 9.

N_FE1 - эквивалентное число циклов шестерни

N_FE1 = 60n₁te_F. (43)

e_F - коэффициент эквивалентности

. (44)

В соответствии с гистограммой нагружения, как и при расчёте на контактную прочность,

. (45)

Эквивалентное число циклов колеса

. (46)

S_F и _Flim - коэффициент запаса прочности и предел выносливости зуба выбираются из таблицы 1.15.

5.3.2. Рабочие напряжения изгиба. Определяется отдельно для шестерни и колеса

. (47)

Y_FS - коэффициент формы зуба

. (48)

X - коэффициент сдвига инструмента.

Z_V - эквивалентное число зубьев

. (49)

Y_ - коэффициент, учитывающий перекрытие зубьев в зацеплении

Для прямозубых . (51)

Для косозубых . (52)

Y_ - коэффициент угла наклона зуба

. (53)

Если Y_ получился меньше 0,7, следует принять

Y_ = 0,7

Рабочие напряжения определяются для каждого зубчатого колеса или для того, у которого меньше отношение

. (54)

Действительный запас усталостной изгибной прочности

. (55)

Значение коэффициента запаса усталостной изгибной прочности показывает степень надёжности в отношении вероятности поломки зуба. Чем больше этот коэффициент, тем ниже вероятности усталостной поломки зуба

5.4. Проверка на контактную статическую прочность.

. (56)

T_max=T_пик - пиковая нагрузка по гистограмме нагружения.

[]_Hmax - допускаемые статические контактные напряжения.

Для улучшенных зубьев

. (57)

Эти допускаемые напряжения предотвращают пластические деформации поверхностных слоев зуба.

Предел текучести _T можно выбрать из таблицы 1.2.

Для поверхностно упрочненных зубьев, в том числе, закалённых ТВЧ

. (58)

Эти допускаемые напряжения предотвращают растрескивание поверхностных слоев зуба.

5.5. Проверка изгибной статической прочности. Проверка делается для шестерни и колеса

. (59)

- допускаемые статические напряжения изгиба. Для улуч­шенных и поверхностно упрочнённых зубьев

. (60)

Проверка по этим допускаемым напряжениям предотвращает мгновенную поломку зуба при перегрузке передачи.

22. Планетарные передачи

Планетарными называют передачи, имеющие зубчатые колёса с перемещающимися осями. Планетарную передачу применяют как редуктор с постоянным передаточным числом, как коробку скоростей, передаточное число в которой изменяется путём поочерёдного торможения различных звеньев (водила или одного из колёс), как дифференциальный механизм. Их успешно применяют в транспортном машиностроении, станкостроении, приборостроении и т.д. Имеется большое количество различных типов планетарных передач, но одноступенчатая планетарная передача (рис. 1) получила самое широкое распространение. Она с успехом применяется как для больших, так и малых мощностей в силовых и кинематических приводах, т.е. не имеет ограничений по применению. КПД передачи 0,96-0,98 . В передачах применяют не только цилиндрические, но и конические колёса. Зубья могут быть прямые и косые. Обычно число сателлитов С=3…6, но встречаются передачи с С>6. Наибольшее распространение получили прямозубые передачи с числом сателлитов С=3.

Планетарная передача состоит из неподвижного центрального колеса 1с наружными зубьями, сателлитов2, неподвижного центрального колеса 3 с внутренними зубьями и водила Н, на котором укреплены оси сателлитов. Сателлиты обкатываются по центральным колесам и вращаются вокруг своих осей, то есть совершают движение, подобное движению планет. Водило вместе с сателлитами вращается вокруг центральной оси. При неподвижном центральном колесе 3 движение может передаваться от центрального колеса1 к водилу Н или от водила к колесу1. В случае неподвижного водила движение может передаваться от колеса1 к колесу3 или от колеса 3 к колесу 1. Планетарную передачу, в которой одно из центральных колёс неподвижно, называют простейшей. В отличие от простейшей планетарную передачу, в которой все зубчатые колёса и водило подвижны (свободны), называют дифференциальной. В дифференциальной передаче одно движение можно раскладывать на два или два движения сложить в одно. Например, движение колеса 3 можно передавать одновременно колесу 1 и водилу Н или от колес 1 и 3 водилу Н.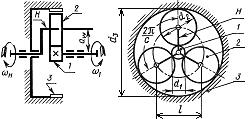

достоинством планетарной передачи является компакт­ность и малая масса. Переход от простых передач к планетарным позволяет во многих случаях снизить массу в 2 ч- 4 и более раз. Это объясняется следующим:

1. Мощность передается по нескольким потокам, число которых равно числу сателлитов (три на рис. 10.40). При этом нагрузка на зубья в каждом зацеплении уменьшается в несколько раз.

Внутреннее зацепление (g и Ь) обладает повышенной нагрузоч­ной способностью, так как у него больше приведенный радиус кри­визны в зацеплении [см. знаки ± в формуле

2. Планетарный принцип позволяет получать большие передаточ­ные отношения (до тысячи и больше) без применения многоступенча­тых передач.

3. Малая нагрузка на опоры, так как при симметричном располо­жении сателлитов силы в передаче взаимно уравновешиваются. Это снижает потери и упрощает конструкцию опор.

К недостаткам планетарных передач относятся повышенные тре­бования к точности изготовления и монтажа.

Планетарные передачи широко применяют в транспортном маши­ностроении, станкостроении, приборостроении и т. д. Внедрение пла­нетарных передач во все области машиностроения и приборостроения является большим резервом в развитии зубчатых передач. Во многих случаях оказываются целесообразными сочетания зубчатых планетар­ных передач с фрикционными, гидравлическими и т. п.

При исследовании кинематики планетарных передач широко ис­пользуют метод остановки водила — метод Виллиса

Всей планетарной передаче мысленно сообщается вращение с ча­стотой вращения водила, но в обратном направлении. При этом водило как бы затормаживается, а все другие звенья освобождаются. Полу­чаем так называемый обращенный механизм , пред­ставляющий собой простую передачу, в которой движение передается от а кb через паразитное колесо g. Частоты вращения зубчатых колес обращенного механизма равны разности прежних частот вращения и частоты вращения водила. В качестве примера проанализируем кине­матику передачи, изображенной на рис. 10.40. Условимся приписы­вать частотам вращения индекс звена (п_а, п_н и т. д.), а передаточные отношения сопровождать индексами в направлении движения и индек­сом неподвижного звена .

В планетарных передачах существенное значение имеет знак пере­даточного отношения. Условимся, что при i > 0 — вращение ведущего и ведомого звеньев происходит в одном направлении; при г С 0 — вращение противоположное. В рассматриваемом примере колеса а и b вращаются в разных направлениях, а потому < 0.

Переходя к реальному механизму, у которого в большинстве слу­чаев практики колесо b закреплено, а — ведущее и Н — ведомое, на основе формулы (10.65) при п_ь = 0 получаем

i_ah^b=na/nh=1+zb/zh

Частоту вращения сателлита определим из равенства (na-nh)/(ng-nh)=Iab^h=-zg/za

При заданных па и nh определяют пд или (ng — nh) как частоту вращения сателлита относительно водила или от¬носительно своей оси (используют при расчете подшипников).

Iha^b=za/(za+zb),

23. Червячная передача относится к передачам зацепления с перекрещиваемся осями валов. . Угол перекрещивания обьино равен 90°. Возможны и другие углы, отличные от 90°, однако такие пере­дачи встречаются редко.

Движение в червячных передачах осуществляется по принципу винто­вой пары. Винтом является червяк, а колесо подобно сектору, вырезан­ному из длинной гайки и изогнутому по окружности.

В червячной передаче, так же как и в зубчатой, различают диаметры начальных и делительных цилиндров : d_wl, d_w2 — начальные диаметры червяка и колеса; d_lt d% — делительные диаметры червяка и колеса.

В передачах без смещения d_wl = d_lt d_w2 = d₂. Точка касания начальных цилиндров является полюсом зацепления.

Шаг р_х винтовой нарезки червяка (см. рис. 11.4) называется шагом зацепления, а отношение т = р_х1л — модулем зацепления в осевом сечении червяка.

Такие же измерения имеет и нарезка червячного колеса. Резьба червяка может быть однозаходной или многозаходной. Число заходов червяка обозначают г_х. На практике наиболее распространены г_х = = 1; 2 и 4. Число зубьев колеса обозначают z₂.

Червяки различают по следующим признакам: по форме поверх­ности, на которой образуется резьба — цилиндрические (рис. 11.3, о) и глобоидные (рис. 11.3, б) ¹; по форме профиля резьбы — с прямолинейным (рис. 11.4, а) и криволи­нейным (рис. 11.4, б) профилем в осевом сечении.

До настоящего времени на практике наиболее распространены цилиндрические червяки с прямолинейным профилем в осевом сече­нии. В торцевом сечении витки очерчены архимедовой спиралью, отсюда название — архимедов червяк

КИНЕМАТИКА ЧЕРВЯЧНОЙ ПЕРЕДАЧИ

В червячной передаче в отличие от зубчатой окружные скорости Oj и v₂ не совпадают (см. рис. 11.2). Они направлены под углом 90° и различны по величине. Поэтому червячная передача имеет следующие особенности: передаточное отношение не может быть выражено отно­шением djdi, в относительном движении начальные цилиндры не обка­тываются, а скользят.

Передаточное отношение

При одном обороте червяка колесо повернется на угол, охватываю­щий число зубьев колеса, равное числу заходов червяка. Для полного оборота колеса необходимо zjz_t оборотов червяка, т. е.

i = n₁/n₂ = z₂/z₁. (11-7)

Число заходов червяка выполняет здесь роль числа зубьев шестерни в зубчатой передаче. Так как г₁ может быть небольшим и часто равным единице (чего не может быть у шестерни), то в одной червячной паре можно получить большое передаточное отношение. Это и является основным достоинством червячных передач.

В силовых червячных передачах наиболее распространены i — 10 -5- -ь 60 (80) ²; в кинематических цепях приборов и делительных меха­низмов встречаются i до 300 и более.

Ведущим в подавляющем большинстве случаев является червяк.

Скольжение в зацеплении

При движении витки червяка скользят по зубьям колеса, как в винтовой паре. Скорость скольжения v_s направлена по касательной к винтовой линии червяка. Как относительная скорость она выра­ жается через абсолютные скорости червяка и колеса, которые в дан­ном случае являются окружными скоростями i>_x и v₂

ОЦЕНКА И ПРИМЕНЕНИЕ

На основе вышеизложенного можно отметить следующие основные преимущества червячной передачи:

а) возможность получения больших передаточных чисел в одной паре;

б) плавность зацепления и бесшумность работы;

в) возможность самоторможения (при низком к. п. д.).

Недостатки этой передачи следующие: сравнительно низкий к. п. д.;

повышенный износ и склонность к заеданию; необходимость приме­нения для колес дорогих антифрикционных материалов (бронза); повышенные требования к точности сборки (точное a_w, совпадение главных плоскостей колеса и червяка).

Червячные передачи дороже и сложнее зубчатых, поэтому их применяют, как правило, при необходимости передачи движения между перекрещивающимися валами, а также в делительных меха­низмах, где необходимо большое передаточное отношение. Червячные передачи применяют в подъемно-транспортных машинах, станкострое­нии, автомобилестроении и т. д. Пониженный к. п. д. и склонность червячных передач к заеда­нию ограничивают их применение областью низких и средних мощ-« ностей. Мощность червячных передач обычно не превышает 50— 60 кВт.

При больших мощностях и длительной работе потери в червячной передаче столь существенны, что ее применение становится невыгод­ным.

24. В зацеплении червяка и червячного колеса (рис.13.6) действуют силы:

круговая сила на червячном колесе (осевая на червяке): Fa1=Ft2=2T2/d2

круговая сила на червяке (осевая на колесе): Fa1=Ft1=2T1/d1

радиальная сила Fr=Ft2*tga

нормальная сила Fn`=Ft2/cos a

С учетом угла наклона (гамма) зубцов колеса нормальная сила может быть определена как

Fn=Fn`/cos y=Ft2/(cos a *cos y)

Основные критерии работоспособности и расчета. Червячные передачи рассчитывают по напряжениям изгиба и контактным напряжениям. Здесь чаще наблюдается износ и заедание. Это связано с большими скоростями скольжения и неблагоприятным направлением скольжения относительно линии контакта. Для предупреждения заедания применяют специальные антифрикционные пары материалов: червяк — сталь, колесо — бронза или чугун.

25. материалы :

В связи с высокими скоростями скольжения и неблагоприятными условиями смазки материалы червячной пары должны обладать антифрикционными свойствами, износостойкостью и пониженной склон­ностью к заеданию.

Червяки современных передач изготовляют из углеродистых или легированных сталей (см. табл. 10.12). Наибольшей нагрузочной способностью обладают пары, у которых витки червяка подвергают термообработке до высокой твердости (закалка, цементация и пр.) с последующим шлифованием или полированием.

Червячные колеса изготавливают преимущественно из бронзы, реже из латуни или чугуна. Оловянистые бронзы типа ОФЮ-1, ОНФ и другие считаются лучшим материалом для червячных колес, однако они

дороги и дефицитны. Их применение ограничивают наиболее ответст­венными передачами с большими скоростями скольжения (u_s до 25 м/с).

Применяют заменители оловянистых бронз, например сурьмяно- кикелевые и свинцовистые бронзы.

Тепловой расчет

Механическая энергия, потерянная в передаче, превращается в тепловую и нагревает передачу. Если отвод тепла недостаточный, передача перегревается и выходит из строя.

Количество тепла, выделяющегося в передаче, ккал/ч

Q = 860(1 — µ) N_u (11.23)

где N_t — мощность на входном валу, кВт; г] — к. п. д. передачи.

Через стенки корпуса редуктора тепло отдается окружающему воздуху — происходит естественное охлаждение. Количество тепла, отданного при этом,

Q1 = Kt(t1-to)S,

где S — поверхность охлаждения, м2; tt — внутренняя температура редуктора или температура масла, °С; t₀ — температура окружающей среды (воздуха), °С; К_т — коэффициент теплоотдачи, ккал/м² -ч -град.

КПД передачи

ή= T2*w2/( T1*w1)= Ft2*d2*w2/(Ft1*d1*w1)

W1,w2-угловая скорость

окончательную форму для определения КПД

ή=tgy/ tg(y+ф)

ф-сведенный угол трения

С учетом затраты мощности в подшипниках и на перемешивание смазочного масла в передаче общий КПД определяют за формулой

КПД увеличивается с увеличением числа заходов червяка (увеличивается ) и с уменьшением коэффициента трения или угла трения ф. Если ведущим является колесо, то меняется направление сил и тогда получим

ή=(0,95…0,96)tgy/ tg(y+ф)

Тепловой баланс при устойчивом режиме работы

∆P=Ф=КА(t_m-t₀)

Ф- епловая мощность, которая выделяется у воздуха поверхностью корпуса;К- коэффициент теплопередачи,А- площадь поверхности; t₀- температура среды, в котором работает передача.

t_m=t0+P1( 1-ή)/(КА)- Температура смазочного масла

26.

1	2	3
2.	Число зубьев червячного колеса z2	z2=z1i; z228
3.	Предварительный КПД()	См. табл.8
4.	Вращающий момент Т1	Т1=Р1/1; 1=n1/30
5.	Вращающий момент Т2	T2=T1i
6.	Предварительная скорость скольжения vs	vs4,510-4n1
7.	Материал и термическая обработка червяка	См. табл.1
8.	Материал колеса и способ отливки	См. табл.2
9.	Механические характеристики червячного колеса	См. табл.2
10.	Время работы передачи Lh	Lh=L365Kгод24Kсут
11.	Ресурс передачи в числах циклов	Nk=60n2cLh; c=1; n2=n1/i
12.	Коэффициент эквивалентности H	См. табл.4
13.	Эквивалентное число циклов нагружения зубьев червячного колеса NHE	NHE=HNk
14.	Коэффициент долговечности KHL	KHL=
15.	Допускаемое контактное напряжение [H]	См. табл.6
16.	Предельное допускаемое напряжение [H]	См. табл.6
17.	Коэффициент эквивалентности F	См. табл.4
18.	Эквивалентное число циклов нагружения NFE	NFE=FNk
19.	Коэффициент долговечности KFL	KFL=
20.	Допускаемое напряжение изгиба [F]	См. табл.7
21.	Предельное допускаемое напряжение [F]max	См. табл.7
22.	Предварительный коэффициент диаметра червяка q	См. табл.9 Условие жесткости червяка q/z2=0,22…0,4
1	2	3
23.	Приведенный модуль упругости Епр	МПа
24.	Межосевое расстояние aw	Расчетную формулу см. табл.3. Полученное значение aw округляют по ряду Ra 40…80, 85, 90, 95, 100, 105, 110, 120, 125, 130, далее через 10 до 260 и т.д.
25.	Осевой модуль m	m=2aw/(q+z2) Полученное значение m округляем до стандартного значения (см. табл.9).
26.	Коэффициент смещения x	x=aw/m-0,5(q+z2) x1 (см. табл.10)
27.	Делительный диаметр червяка d1	d1=mq
28.	Делительный диаметр червячного колеса d2	d2=mz2
29.	Угол подъема винтовой линии червяка 	tg=z1/q
30.	Окружная скорость червяка V1	V1=d1n1/60
31.	Уточняем скорость скольжения Vs	Vs=V1/cos Уточняем выбор материала колеса в зависимости от Vs (см.табл.2). При смене материала необходимо сделать перерасчет.
32.	Уточненное [H] с учетом фактической Vs	См. табл.6
33.	Окружная скорость червячного колеса V2	V2=d2n2/60
34.	Коэффициент динамической нагрузки Kv	Kv=1 при Vs  3м/с Kv=1…1,3 при Vs  3м/с
35.	Коэффициент концентрации нагрузки K	K=1 при постоянной нагрузке K=1,05…1,2 при переменной нагрузке
36.	Коэффициент деформации червяка 	См. табл.11
		Продолжение табл.16
1	2	3
37.	Коэффициент режима работы передачи X	См. табл.12
38.	Уточненный коэффициент концентрации нагрузки K	K=1+(z2/)3(1-X)
39.	Коэффициент расчетной нагрузки KH	KH=KvK
40.	Коэффициент торцевого перекрытии 	=1,8…2,2 =
41.	Угол обхвата колесом червяка 2	21101,75рад
42.	Коэффициент, учитывающий уменьшение длины контактной линии 	0,75
43.	Фактическое контактное напряжение H	H= Допустима недогрузка не более 20%, перегрузка – не более 5%. Выход за указанные пределы величины H требует уточнения ранее найденных параметров передачи.
44.	Нормальный модуль mn	mn=m/cos
45.	Окружная сила на червячном колесе	Ft2=
46.	Ширина венца червячного колеса b2	b2=0,355aw при z1=1;2 b2=0,315aw при z1=4 Округляем до значения из ряда Ra 40
47.	Число зубьев эквивалентного колеса zv	zv=z2/cos3
48.	Коэффициент формы зуба YF	Интерполируя данные табл.13
49.	Коэффициент расчетной нагрузки KF	KF=KH
50.	Прочность зубьев по напряжениям изгиба F	F=
51.	Угол трения 	См. табл.14
52.	Уточненный 	=tg/tg(+) отклонение до 10% допустимо.
		Продолжение табл.16
1	2	3
53.	Фактическое передаточное число	iф=z2/z1; i  5% для одноступенчатых редукторов; i  8% для двухступенчатых редукторов.
54.	Максимальное контактное напряжение Hmax	Hmax=
55.	Максимальное напряжение изгиба Fmax	Fmax=
56.	Осевая сила на колесе Fa2	Fa2=Ft1=
57.	Радиальная сила Fr	Fr=Ft2tg/соs; =20; tg=0,364
58.	Диаметр вершин витков червяка da1	da1=d1+2m
59.	Диаметр впадин витков червяка df1	df1=d-2,4m
60.	Длина нарезанной части червяка b1	См. табл.10
61.	Диаметр вершин зубьев колеса da2	da2=d2+2m(1+x)
62.	Диаметр впадин зубьев колеса df2	df2=d2-2m(1,2-x)
63.	Диаметр колеса наибольший daM2	daM2da2+6m/(z1+2)
64.	Ширина венца колеса b2	b2 = 0,355аw при z1 =1,2 b2 = 0,315аw при z1 = 4
65.	Степень точности	7– ая при vs 10 м/с 8– ая при vs 5 м/с 9– ая при vs 2 м/с |
66.	Тепловая мощность	W=P1(1-), P1 – мощность на валу червяка
67.	Коэффициент теплоотдачи	К=12…18; К=24…50 при обдуве вентилятором (большие значения при хороших условиях естественного охлаждения)
68.	Температура масла	t1=60…70C
69.	Температура окружающей среды (воздуха)	t0=20С

Продолжение табл. 16

1	2	3
70	Площадь поверхности охлаждения	Приближенно площадь А (м2) табл.15. Поверхность А (м2) охлаждения корпуса равна сумме поверхности всех его стенок, за исключением поверхности дна. Размеры стенок определяют по чертежу.
71.	Мощность теплоотдачи W1	W1=K(t1-t0)A
72.	Проверка на нагрев	W W1 В противном случае необходимо применять искусственное охлаждение.

27.Цепная

основана на зацеплении цепи 1 и звездочек. Отсутствие скольжения и буксования обес­печивает постоянство передаточного отношения (среднего за оборот) и возможность работы при значи­тельных кратковременных пере­грузках.

Принцип зацепления не тре­бует предварительного натяже­ния цепи, в связи с чем умень­шается нагрузка на валы и опоры.

Угол охвата звездочки цепью не имеет столь решающего зна­чения, как угол обхвата шкива ремнем. Поэтому цепные пере­дачи могут надежно работать при малых межосевых расстояниях и при больших передаточных отно­шениях, а также передавать мощ­ность от одного ведущего вала 1 нескольким ведомым 2 .

Однако цепные передачи имеют и некоторые недостатки. Основной причиной этих недостатков является то, что цепь состоит из отдель­ных звеньев и располагается на звездочке не по окружности, а по много­угольнику. С этим связаны износ шарниров цепи, шум и дополни­тельные динамические нагрузки. Затрудненный подвод смазки к шар­нирам сокращает срок службы передачи.