4. Приведение математической формулировки краевой задачи к записи в безразмерных переменных.

Пусть поверхность твердого тела омывается несжимаемой жидкостью, температура и скорость которой вдали от тела постоянны и равны соответственно t₀ и . Размер тела l₀ задан. Температура поверхности тела равна t_c. Для определенности примем, что t_c>t₀. Будем полагать, что физические параметры жидкости постоянны. Теплота трения не учитывается. Рассматриваемый процесс является стационарным.

Расположим оси координат так, как показано на рис. 5.1. Примем, что ось Oy нормальна к поверхности тела, а ось Ox направлена вдоль тела и вертикальна.

При этом g_x=g, а проекции вектора сил тяжести (или подъемной силы) на оси Oy и Oz будут равны нулю (g_y=g_z=0).

Р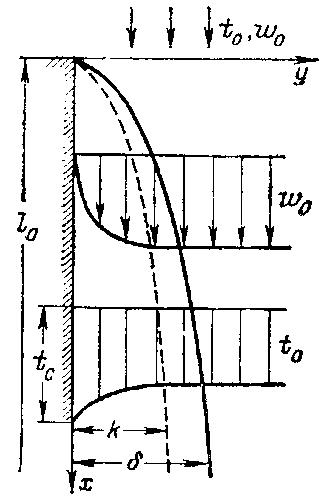 азмер тела вдоль оси Oz намного больше l₀.

В уравнениях и условиях однозначности можно различить три вида величин:

– независимые переменные – это координаты x и y.

– зависимые переменные – это 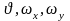; зависимые переменные однозначно определяются значениями независимых переменных, если заданы величины, входящие в условия однозначности;

– постоянные величины – это и др.; они задаются условиями однозначности и для определенной задачи являются постоянными, не зависящими от других переменных.Обозначим безразмерные величины

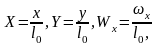
(б)

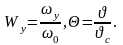
Тогда

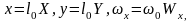
(в)

.

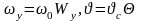уравнения энергии : 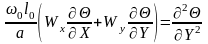. (5.1)

уравнение движения: .

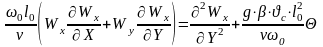уравнения сплошности

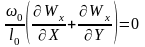
Коэффициент теплоотдачи может быть определен по уравнению

.

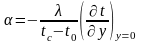Приводя к записи в безразмерных переменных, получаем

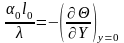. (5.4)

5. Критерии подобия и критериальные уравнения.

Помимо безразмерных величи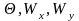н и безразмерных координат, составленных из однородных физических величин, в уравнения входят также безразмерные комплексы, состоящие из разнородных физических величин

.

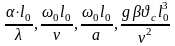Этим комплексам, называемым числами подобия, присвоены имена ученых, внесших значительный вклад в развитие теплотехники и механики.

Первый из этих безразмерных комплексов обозначают

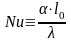(5.5)

и называют числом Нуссельта или безразмерным коэффициентом теплоотдачи. Число Нуссельта характеризует теплообмен на границе стенка – жидкость.

Безразмерный комплекс

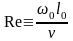(5.6)

называют числом Рейнольдса. Оно характеризует соотношение сил инерции и сил вязкости.

Третий безразмерный комплекс обозначают

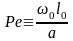(5.7)

и называют числом Пекле. Его можно преобразовать следующим образом

,

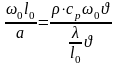здесь числитель характеризует теплоту, переносимую конвекцией, а знаменатель – теплоту, переносимую теплопроводностью.

Безразмерный комплекс

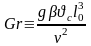(5.8)

называют числом Грасгофа. Оно характеризует подъемную силу, возникающую в жидкости вследствие разности плотностей.

Безразмерный комплекс

число Архимеда .

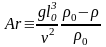Используя введенные обозначения, систему безразмерных диффе­ренциальных уравнений можно записать в следующем виде

;

;

;

.

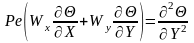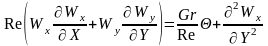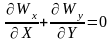Безразмерные величины Θ, W_х, Wy, X, Y, Nu, Re, Ре, Gr можно рас­сматривать как новые переменные. Их можно разделить на три группы:

– независимые переменные – это безразмерные координаты X, У;

– зависимые переменные – это Nu, Θ, W_x, W_y; они однозначно определяются значениями независимых переменных при определенных значениях величин, входящих в условия однозначности;

– постоянные величины – это Ре, Re, Gr;

В результате можно написать

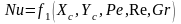, (5.14)

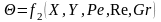, (5.15)

, (5.16)

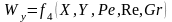. (5.17)

Безразмерный комплекс

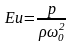(5.18)

называют числом Эйлера. Это число характеризует соотношение сил давления и сил инерции.

Число Ре, полученное при приведении к безразмерному виду урав­нения энергии, можно представить как произведение двух безразмерных переменных

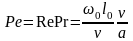. (5.19)

Безразмерная величина 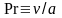представляет собой новую перемен­ную, называемую числом Прандтля. Число Прандтля целиком со­ставлено из физических параметров, и поэтому и само является физи­ческим параметром. Его можно записать и в виде

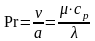. (5.20)

Числу Прандтля можно придать определенный физический смысл. Уравнение энергии

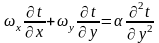
и уравнение движения

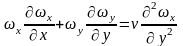
по записи аналогичны. При расчетные поля температур и скоро­стей будут подобны, если только аналогичны и условия однозначности.

Для капельных жидкостей число Прандтля зависит от температуры, для воды с увеличением температуры вязкость воды уменьшается и число Прандтля тоже уменьшается.

Число Pr газов практически не зависит ни от температуры, ни от давления и для данного газа является величиной постоянной, определяемой атомностью газа.

Число Pr является мерой подобия полей температур и скоростей.

Учитывая, что Pe = Re Pr, уравнения подобия можно записать в виде

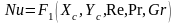, (5.21)

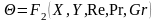, (5.22)

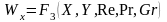, (5.23)

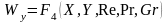. (5.24)

Исходя из уравнений (5.14) – (5.17) и (5.21) –(5.24), безразмер­ные переменные можно разделить на два вида:

– определяемые – это числа, в которые входят искомые зависи­мые переменные; в рассматриваемом случае зависимыми являются , следовательно, определяемыми являются Nu, Θ, W_x и W_y;

– определяющие – это числа, целиком составленные из незави­симых переменных и постоянных величин, входящих в условия однознач­ности; в рассматриваемом случае определяющими являются X, У, Re, Pr (или Ре) и Gr.