2. Определение длины переходной кривой.

1.2.1 Определение длины переходной кривой из условия не превышения допустимого уклона отвода возвышения наружного рельса.

Переходные кривые обеспечивают плавный переход подвижного состава из прямой в круговую кривую или из круговой кривой одного радиуса с одним возвышением в кривую другого радиуса с другим возвышением наружного рельса.

В пределах переходной кривой (ПК) плавно нарастает кривизна К = 1/ρ пути за счет изменения переменного радиуса ρ от ρ = ∞ в начале переходной кривой (НПК) до ρ = R в конце переходной кривой (КПК). В пределах ПК плавно увеличивается возвышение наружного рельса от 0 в НПК до h в КПК; делается отвод уширения колеи, если последнее имеется в круговой кривой.

Основные требования к устройству и содержанию ПК сводятся к тому, чтобы появляющиеся, развивающиеся и исчезающие силовые факторы (ускорения, силы, моменты) в пределах длины l ПК изменялись постепенно и монотонно, с заданным графиком, а в начале и в конце ПК они были равны нулю.

(1.4)

где ℓ₁ – длина переходной кривой, м

h – возвышение наружного рельса, м

i – уклон отвода, ‰ (i = 0,9‰, т.к V_мах 110 км/ч)

2. Определение длины переходной кривой из условия скорости подъема колеса по наружному рельсу.

(1.5)

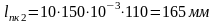
3. Определение длины переходной кривой из условия величины нарастания непогашенных поперечных ускорений.

(1.6)

где _доп = 0,7 м./с²

= 0,4 м./с². – допускаемая величина непогашенных поперечных

ускорений.

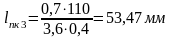
Исходя из 3-х условий, выбираем наибольшее значение l = 166мм

Принимаем длину переходной кривой l = 180 мм.

1.2.4 Разбивка переходных кривых.

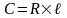(1.7)

(1.8)

где C – параметр переходной кривой,

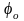= угол поворота в пределах переходной кривой.

Определяем параметр С.

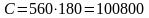
Возможность разбивки кривой способом сдвижки определяется из условия:

2 ≤ β

где β – угол поворота кривой.

1.2.4.1. Определение вида переходной кривой и координаты ее для разбивки

в прямоугольной системе.

Проверка проводится исходя из условия:

Вывод: условие выполняется, разбивка переходной кривой производится

по закону кубической параболы в соответствии с выражением:

Пользуясь этим уравнением, вычислим ординаты переходных кривых через интервалы 10 м. Расчеты сводятся в таблицу.

l	y
10	0,00165
20	0,0132
30	0,0446
40	0,1058
50	0,2066
60	0,3571
70	0,5671
80	0,8465
90	1,2053
100	1,6534
110	2,2007
120	2,8571
130	3,6326
140	4,5370
150	5,5803
160	6,7724
170	8,1233
180	9,6428

Расчеты координат для разбивки переходной кривой.