
Об основаниях теории множеств
Коэн П. Дж.
Высказываться о философских проблемах теории множеств, — разумеется, не совсем то, что высказываться о самой теории множеств. Я, по крайней мере, в этом положении чувствую себя непривычно и неловко. Я остро ощущаю тщетность попыток сформулировать позицию, приемлемую для всех или хотя бы для многих, и одновременно сознаю непоследовательность и трудности моей собственной точки зрения. Конечно же, те, кто до меня совершали этот рискованный переход от математики к философии, обычно шли на это на более позднем этапе своей научной карьеры. Наконец, к довершению трудностей, почти немыслимо добавить что-нибудь новое к этому старому спору. В самом деле, я склонен думать, что на такие фундаментальные вопросы любые технические достижения почти не проливают света — хотя, конечно, они могут повлиять на распространение той или иной точки зрения.
Но вот, невзирая на все эти оговорки, я чувствую некоторое воодушевление от возможности высказать свои мысли, надеюсь, не слишком догматично, и указать на обстоятельства, на которые, пожалуй, следует указать. Фундаментальные открытия в логике были сделаны так недавно, что мы ещё в состоянии разделять глубокое волнение от этих поисков вслепую. Всплеск исследовательской активности в теории множеств, о котором свидетельствует нынешняя встреча, возможно, усиливает наш энтузиазм. Тон сегодняшних философских дискуссий, однако, как будто изменился. Возможно, математики полностью выложились в неистовых спорах прошлого, или их аудитория утомилась от полемики, — как бы то ни было, сейчас принято формулировать свою точку зрения, но не пытаться тут же обращать слушателя в собственную веру. В этом духе собираюсь выступить и я, чистосердечно уверив слушателей в своей терпимости к чужим взглядам.
Хотя я не представляю себе, что можно было бы назвать «истинным» прогрессом в основаниях математики, очень интересно проследить с точки зрения историка, как высказывались на эту тему разные поколения, и попытаться угадать, как окрашивал их мнения дух времени. Сам я предпочитаю рассматривать математическую деятельность как сугубо человеческое предприятие, а отнюдь не как безличное наступление науки, свободной от всех человеческих слабостей. Так, позиция по вопросам оснований, которую занимает тот или иной математик, в большой мере определяется его воспитанием и окружением. Мне кажется, что желание принять принципы, ведущие к интересной и красивой математике, в прошлом безусловно преодолело разнообразную и серьёзную критику. В этом докладе я хотел бы указать на аналогичные тенденции, которые существуют сегодня.
Прежде в центре споров находились многие вопросы, о которых я без особых на то причин высказываться не стану, например, закон исключённого третьего. Хотя он и связан с проблемами теории множеств, скажем, через использование непредикативных определений, сам по себе он не относится к теории множеств и здесь обсуждаться не будет. Я не намерен заниматься также всеми остальными проблемами законности применения исчисления предикатов, вопросами о природе формализации математики и чисто философскими вопросами, мало связанными со спецификой математического знания. Для меня важнейшей проблемой представляется существование бесконечных совокупностей. Отношение к бесконечным множествам по традиции было критерием размежевания математиков. Знаменитые логические антиномии никогда не играли заметной роли в математике просто потому, что они не имели ничего общего с обычно используемыми рассуждениями. Никогда не рассматривались все мыслимые объекты универсума, длины описаний и т.п. Все эти трудности принадлежат, собственно, истории развития понятия формальной системы. Подобно этому, парадоксы Зенона вовсе не производят на нас впечатления демонстрации серьёзных трудностей, ради чего они и были придуманы. В общем, я склонен считать, что многие из этих проблем исторически связаны с переходным периодом от классической философии к нынешней математике.
Нет сомнения, что в ряде случаев бесконечными множествами можно пользоваться без особых опасений. Очевидно, всё равно, сказать ли, что некоторым свойством обладают все целые числа или все элементы множества целых чисел. Точно также, сказать, что n принадлежит множеству четных чисел, всё равно, что сказать «n чётное». Иными словами, можно заменить использование некоторых множеств названием соответствующих свойств. Если бы это удавалось сделать всегда, у нас осталось бы мало оснований для беспокойства. В теории чисел, желая избежать апелляции к понятию произвольного множества целых чисел, мы должны формулировать принцип индукции отдельно для каждого свойства, которое можно выразить. Однако чрезвычайная сложность теории множеств, особенно её непредикативный характер, мешают просто представлять себе множества как стенограмму свойств. Всё же самые мощные и характерные аксиомы теории множеств — аксиомы степени и подстановки — описывают множества свойствами, а гёделевская теория конструктивных множеств показывает, что некоторую модель теории множеств можно получить, рассматривая вообще только множества, в некотором смысле отвечающие свойствам. То обстоятельство, что аксиома подстановки есть на самом деле бесконечная схема аксиом, в определённых отношениях является недостатком. Действительно, создаётся впечатление, что мы позволяем рассматривать лишь некоторые свойства, вместо того чтобы указать фундаментальное описание способов построения множеств. Конечно, всё это связано с теоремой Гёделя о неполноте, согласно которой никакая конечно аксиоматизируемая система не может быть полной. Эта теорема является величайшим препятствием для любой попытки полностью понять природу бесконечных множеств. Одновременно, показывая, что высшие бесконечности отражаются в теории чисел, ибо позволяют нам доказывать недоказуемые без них утверждения, теорема Гёделя чрезвычайно затрудняет отстаивание той точки зрения, что высшие бесконечности можно попросту отвергнуть. Наша привычка к теореме о неполноте не должна мешать нам постоянно видеть эту фундаментальную недостаточность всех формальных систем, которая имеет гораздо более далеко идущие последствия, чем независимость частных утверждений вроде гипотезы континуума. Именно это лежит в основе моего пессимистического мнения о том, что любое техническое достижение и в будущем не прольёт света на основные философские проблемы.
Рядовому математику, желающему лишь увериться в том, что его дело стоит не на песке, самым привлекательным способом избежать трудностей может показаться программа Гильберта. С этой точки зрения математика есть формальная игра, в которой следует заботиться лишь о непротиворечивости. С течением времени, когда операционный подход распространился на другие области, скажем, физику, привлекательность этой позиции, возможно, увеличилась. Можно работать лишь с непосредственно данными объектами, а в математике к таким относятся скорее формальные языки, чем бесконечные множества. Действительно, гильбертовская программа формализации по-прежнему остаётся единственной вполне точной (мы не говорим правильной) точкой зрения в этих вопросах. Вот убедительный пример того, как само по себе течение времени мало повлияло на появление новых и оригинальных концепций в основаниях. Но, разумеется, формализму присущи свои трудности, и прежде чем вернуться к нему, мы рассмотрим его главную альтернативу, точку зрения, которую можно назвать платонизмом, а мы предпочтём называть реализмом.
Сторонник реалистической философии полностью принимает ценности традиционной математики. Все вопросы типа гипотезы континуума допускают положительный или отрицательный ответ в реальном мире безотносительно к их независимости от той или иной системы аксиом. Вероятно, большинство математиков предпочли бы эту точку зрения. В ней начинают сомневаться лишь после осознания некоторых трудностей теории множеств. Если эти трудности особенно смущают математика, он спешит под прикрытие формализма, предпочитая, однако, в спокойное время обретаться где-то между двух миров, наслаждаясь лучшим, что есть в обоих. Главное преимущество реализма состоит в том, что он избавляет от необходимости обосновывать аксиомы теории множеств. Нет нужды устанавливать их непротиворечивость и, что кажется мне столь же важным, нет нужды объяснять, почему именно эти аксиомы оказались настолько успешными и достойными специального внимания. Соответственно самая большая слабость формализма состоит в невозможности объяснить, почему аксиомы теории множеств, предположительно не отражающие никакой реальности, способны доказывать арифметические утверждения, не доказуемые с помощью более финитистских средств. Слабость, которую, как я полагаю, вынужден будет признать любой реалист, состоит в неспособности объяснить нескончаемую последовательность новых аксиом, вроде высших аксиом бесконечности. Несомненно, самый закоренелый реалист содрогнётся, рассматривая кардиналы достаточно недостижимого типа. А есть ещё аксиомы, как аксиома об измеримом кардинале, которые сильнее всех предложенных аксиом бесконечности и относительно которых, по-видимому, нет ни малейших интуитивно убедительных свидетельств в пользу принятия или отвержения. Недавние результаты о независимости также бросают вызов реалистической позиции. Хотя некоторые чувствуют, что какая-то интуитивно приемлемая аксиома сможет в конце концов разрешить проблему континуума и подобные ей вопросы, нет ни малейшей надежды на такой исход для аксиомы об измеримом кардинале, которую ревностные теоретико-множественники, вероятно, вынуждены будут признать в качестве аксиомы, ни к чему не сводимой. Однако даже в этом отношении позиция реалистов завиднее, чем формалистов, потому что для последних существуют даже неразрешимые теоретико-числовые предложения, скажем, Consis (ZF). Оптимистическая точка зрения реалиста может состоять в том, что утверждение Consis (ZF + измеримый кардинал) как-нибудь сведётся к вопросу о непротиворечивости достаточно сильных предложений того же типа, что аксиомы бесконечности. Самая оптимистическая точка зрения заключается в надежде, что любой вопрос теории чисел решается с помощью подходящей аксиомы бесконечности.
Исторически математика как будто не склонна терпеть неразрешимые предложения. Такое предложение может быть возведено в ранг аксиомы и стать широко принятым после многократного употребления. Такова в общих чертах судьба аксиомы выбора. Я склонен оценить эту тенденцию просто как форму оппортунизма. Разумеется, это безличный и весьма конструктивный оппортунизм. Тем не менее, вера в ценность и важность математики не должна полностью изглаживать из нашего сознания честную оценку беспокоящих проблем. В случае с гипотезой континуума (КГ) эта тенденция может, хотя и с малым вероятием, привести теорию множеств к расщеплению на несколько ветвей в зависимости от принятой мощности континуума. Несколько цинично можно сказать, что оппортунизм решает философские проблемы так, чтобы развитие математики давало заработок возможно большему числу математиков. В последнее время много занимались вопросами независимости в теории множеств. Удивительный эффект состоит в том, что большая лёгкость в обращении с этими вопросами привела к бóльшей вере в «реальность» математических объектов теории множеств. Было бы поистине печально, если бы эта волна успеха закончилась полным пренебрежением к философским проблемам гипотезы континуума и смежных вопросов как непоследовательным. Разумеется, хорошая математика красива, тогда как философские дискуссии по большей части бесплодны и уж, конечно, не красивы.
С реалистической позиции можно гадать о судьбе КГ. Казалось бы, только аксиомы типа аксиомы конструктивности, ограничивающие природу рассматриваемых множеств, могут разрешить её. С другой стороны, мало надежды, что такая аксиома будет принята в качестве интуитивно очевидной. Более правдоподобно, что в качестве аксиомы будет принято её отрицание. Оправдание этого может состоять в том, что континуум, данный как множество всех подмножеств, не может быть достигнут любыми средствами, строящими кардиналы, исходя из меньших, на основе аксиомы подстановки. Таким образом, континуум следует считать большим, чем 1; n, ω и т.д. Разумеется, всё это — чистая спекуляция. Технические последствия принятия различных аксиом, связанных с КГ, уже в какой-то мере привлекли внимание. Хотя эта работа может представлять большую эстетическую ценность, в высшей степени неправдоподобно, что она способна привести к прояснению фундаментальных философских проблем.
К этому моменту должно быть ясно, что я выбираю формализм. Едва ли можно назвать этот выбор мужественным, — вероятно, большинство известных математиков, высказывавшихся на этот счёт, в той или иной форме отвергали позиции реализма. Сформулировать свою точку зрения совершенно явно меня побудила речь Абрахама Робинсона в Иерусалиме в 1964 г. Она вынуждает принять на себя тяжёлую ношу. Едва ли не тяжелей остального необходимость допустить, что КГ, — возможно, первый приходящий в голову важный вопрос о бесконечных множествах — не имеет внутреннего смысла. Жизнь была бы гораздо приятнее, не будь гильбертовская программа потрясена открытиями Гёделя. Я твёрдо верю, что программа Гильберта ни в каком смысле не может быть восстановлена. Доказательства непротиворечивости всегда вызывают острую неудовлетворённость и явно сохраняют черты порочного круга.
Как уже говорилось, величайшая слабость формализма состоит в необходимости объяснить успешность чисто формальных аксиом, составляющих теорию множеств. Моя точка зрения, неоднократно выражавшаяся и прежде, состоит в том, что эти аксиомы экстраполируют язык более финитистской математики. Тенденции к такому расширению очень сильны. Для пояснения позвольте мне сначала напомнить ситуацию, в которую рано или поздно попадает каждый логик. Беседуя с квалифицированным математиком, не знающим логики, обнаруживаешь трудность общения, едва лишь речь заходит о формальных системах и анализе структуры формул. Математик гораздо охотнее будет говорить о моделях какой-нибудь системы аксиом, нежели о множестве всех формул, доказуемых исходя из них. Разумеется, согласно теореме о полноте обе точки зрения эквивалентны. Однако имеется естественная тенденция заменить обсуждение методов и предложений обсуждением подходящих абстракций, рассматриваемых как «объекты» теории. Например, развитие вещественного анализа в XIX веке было отмечено изменением отношения к понятию функции. Сначала функция рассматривалась как явное правило, сопоставляющее числа числам. В конечном счёте функция стала представляться целостным объектом безотносительно к явному заданию способа её вычислять. Непрерывная нигде не дифференцируемая функция Вейерштрасса приобрела те же права на существование, что и sin x. Когда Кантор впервые обсуждал теорию множеств, возможно, значительная часть сопротивления была вызвана просто мнением, что говорить можно лишь о тех множествах, которые уже были явно определены. Всем нам известно, что точка зрения Кантора восторжествовала полностью. В конечном счёте главной причиной этого было, возможно, удобство. Гораздо проще говорить об абстрактных множествах, чем постоянно заботиться об их построении. Более свежий пример той же тенденции — теория категорий. Здесь говорят, скажем, о категории групп. Можно спросить, в чём преимущество выражения «G есть объект категории групп» перед выражением «G — группа». Простой ответ состоит в том, что перенос методов из одной категории в другую и даже доказательство общих теорем о категориях может подсказать очень полезные идеи. И всё же, если я не ошибаюсь по недостатку сведений о современных течениях, теоретико-множественные трудности работы с категориями не вдохновили многих специалистов по теории множеств и не оказали серьёзного влияния на логику в целом. Таким образом, полностью приняв весьма непредикативную теорию множеств, внутреннюю убедительность которой мы понимаем, мы как логики менее склонны принимать теорию категорий, корни которой лежат в алгебраической топологии и алгебраической геометрии. Хотя, возможно, существующих аксиом бесконечности было бы достаточно для формализации теории категорий, настойчивый специалист по ним мог бы возразить, что сами категории следует считать примитивными объектами. В определённом смысле они подобны классам в теории множеств Гёделя—Бернайса. И в этом случае классы, предназначенные всего лишь для замены бесконечной схемы аксиом Цермело—Френкеля, стали широко приняты как самостоятельные объекты. Другой пример того, как привычка притупляет критические способности, доставляет аксиома о недостижимом кардинале. Её принятие обычно оправдывают чисто отрицательными аргументами; дескать, неразумно считать, что любое множество достижимо. Здесь усматривается аналогия с переходом от конечных множеств к бесконечным. Совершив по индукции трансфинитную последовательность тех или иных операций замыкания, мы якобы всё ещё способны двинуться дальше и найти за этими пределами недостижимый кардинал. Мне кажется, однако, что это неубедительное рассуждение, поскольку оно скорее предназначено оправдать существование стандартной модели теории множеств, а эта гипотеза несравненно слабее. Честнее было бы признать, что недостижимые кардиналы можно принять, ибо, как показал опыт, это не ведёт к противоречиям, и мы развили некоторую интуицию, позволяющую надеяться, что противоречие не появится никогда.
Став на позиции формализма, я чувствую себя обязанным объяснить, почему я не призываю отменить всю инфинитистскую математику. Я хотел бы высказать следующее мнение: мы занимаемся теорией множеств по той причине, что ощущаем наличие неформального доказательства её непротиворечивости. Вот на чём основано это чувство: в каждом конкретном случае мы говорим лишь о специфических множествах, определённых свойствами и, прослеживая противоречие в обратном порядке, мы можем в конце концов свести его к теоретико-числовому. Использование непредикативных определений усложняет задачу интуиции, потому что неограниченная непредикативность определённо ведёт к хорошо известным парадоксам. Всё же обычная аксиома подстановки даёт нам возможность начать с какого-то множества упомянутую выше редукцию, ибо во вновь определяемом множестве каждый элемент должен быть занумерован подходящим элементом множества, построенного раньше. Уже высказав мнение, что техническое развитие не приводит к прояснению основ, я не намерен пытаться дать строгое доказательство непротиворечивости, основанное на каком-нибудь мощном высшем принципе, эквивалентном теории Цермело—Френкеля. Я ограничусь лишь наброском общей схемы, внутри которой развиваются эти интуитивные соображения.
Вот один из способов размышлять о доказательствах непротиворечивости. Начнём с конечного числа аксиом, скажем, S1. Для каждого множества, существование которого постулируется, выберем по символу и подставим его в соответствующее утверждение. Получится новая система утверждений S2. Чтобы перейти к Sk, мы выбираем новые символы для всех множеств, существование которых утверждалось ранее; кроме того, для каждого утверждения вида x A(x) и каждого уже введённого символа c мы добавляем A(c). Предположим, что на некотором шаге появится противоречие между суждениями без кванторов. Для удобства мы можем на некоторых стадиях расщепить вывод на две ветви, добавляя в одной из них A, а в другой ~A. Предположим, что к противоречию приводит и то и другое. Положение дел ещё можно упростить, не добавляя всех суждений, а лишь необходимые. Наша цель — набросать способ уменьшения сложности противоречия. Начнём с символов и ω. Допустим, что на некотором шаге мы встретились с множеством x1, которое определяется частным случаем аксиомы подстановки, отвечающим некоторому свойству. Если другое множество x2 в конца концов появляется в формуле x2 x1, мы можем попытаться исключить x1, заменив его соответствующим свойством x2, и расщепить вывод на две ветви, предположив, что x2 им обладает или нет. Если само множество x1 появляется позже, мы попытаемся заменить его конечным множеством тех его элементов, которые появляются в ходе вывода. Разумеется, чтобы уточнить всё это, необходим анализ непредикативных определений и упорядочение степеней непредикативности. Зная, что теорема о неполноте делает эту задачу по существу безнадёжной, мы не станем ею заниматься. Ключевой пункт состоит в том, что всякий элемент нового множества должен быть связан с некоторым элементом множества, построенного раньше, так что редукцию можно продолжать. В парадоксе Рассела этому мешает круг. Общеизвестно, что Гентцен провёл такое доказательство для теории чисел в пределах ординала ε0. В случае Цермело—Френкеля неясно, можно ли определить аналогичный ординал. Если ответ положителен, было бы интересно изучить его связь с другими известными инвариантами, например, счётным ординалом минимальной модели. Это такой наименьший ординал α, что Mα, множество Гёделя на α-м шаге, является моделью для аксиом Цермело—Френкеля. Ординал из теории вывода должен быть меньше, ибо он «строит» наименьшую нестандартную модель аксиом.
Даже в самом оптимальном случае схема, которую я набросал, позволила бы справиться лишь с проблемами, связанными с аксиомой подстановки. Наша интуиция о недостижимых или измеримых кардиналах ещё недостаточно развита или по крайней мере не поддаётся передаче в общении. Мне кажется, тем не менее, что полезно развивать наше таинственное чувство, позволяющее судить о приемлемости тех или иных аксиом. Здесь, разумеется, мы должны полностью отказаться от научно обоснованных программ и вернуться к почти инстинктивному уровню, сродни тому, на котором человек впервые начинал думать о математике. Лично я, например, не в состоянии отказаться от этих проблем теории множеств просто потому, что они отражаются в теории чисел. Я сознаю, что моя позиция в прагматическом плане мало чем отличается от позиции реализма. Всё же я чувствую себя обязанным сопротивляться великому эстетическому соблазну без околичностей принять множества как существующую реальность.
Читатель безусловно ощутит горечь пессимизма в моих заметках. Математика подобна прометееву труду, который полон жизни, силы и привлекательности, но содержит в самом себе зерно разрушающего сомнения. К счастью, мы редко останавливаемся, чтобы обозреть положение дел и подумать об этих глубочайших вопросах. Всю остальную жизнь в математике мы наблюдаем блестящую процессию и, возможно, сами участвуем в ней. Великие задачи теории множеств, казавшиеся неодолимыми, падают. Изучаются новые аксиомы, всё большие и большие кардиналы становятся доступнее интуиции. Маяк теории чисел сияет над этой зыбью. Когда сомнения начинают одолевать нас (что, я надеюсь, происходит нечасто), мы отступаем под безопасные своды теории чисел, откуда, собравшись с духом, снова бросаемся в неверные воды теории множеств. Такова наша судьба — жить, сомневаясь; преследовать цель, в абсолютности которой мы не уверены; короче, понимать, что наша единственная «истинная» наука имеет всё ту же смертную, возможно, опытную природу, что и все прочие человеческие предприятия.
Поиск кратчайших сетей
Маршалл У. Берн, Рональд Л. Грэм
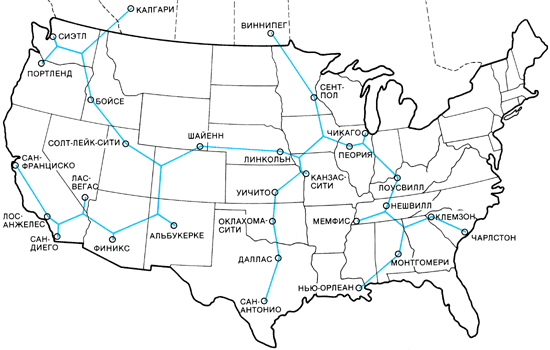
Представим себе такую ситуацию: некая телефонная компании Steiner Telephone Company подсчитала, что можно сэкономить несколько миллионов долларов, если удастся найти кратчайшую из возможных сетей телефонных линий, соединяющих 100 населённых пунктов. Чтобы решить эту задачу, компания заключила контракт с компьютерной компанией Cavalieri Computer Company, располагающей самыми быстродействующими в мире компьютерами и самыми квалифицированными программистами. Через неделю Cavalieri продемонстрировала в действии программу для решения поставленной задачи. Программа действительно нашла кратчайшую сеть для 15 абонентов всего за один час. Steiner заплатила 1000 долл. за программу и пообещала платить по одному центу за каждую секунду машинного времени, которое потребуется компьютеру для полного решения задачи. К тому времени, когда компьютер завершил вычисления для всех 100 абонентов, телефонная компания задолжала компьютерной многие триллионы долларов, а сами абоненты переместились на много километров со своих мест — либо по своему желанию, либо по причине континентального дрейфа!
Может быть, Cavalieri продала Steiner неправильную программу? Попробуем разобраться. Здесь мы столкнулись с одним из примеров так называемой задачи Штейнера, в которой требуется найти кратчайшую сеть прямолинейных отрезков, связывающих между собой заданное множество точек.
|
|
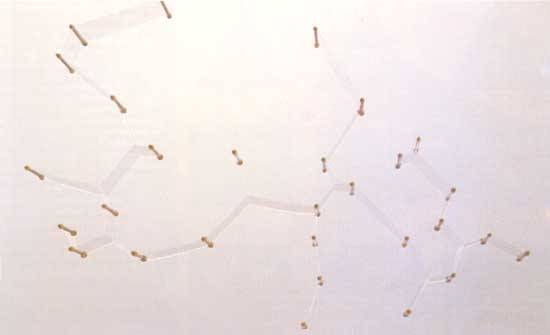
Компьютер из мыльной плёнки (вверху) соревнуется с электронным компьютером (внизу), отыскивая кратчайшую сеть, связывающую между собой 29 городов. Компьютер из мыльной плёнки, в котором расположение штырьков моделирует географию городов, минимизирует длину плёночных соединений в локальной области. Он даёт короткую сеть, но необязательно кратчайшую. Электронный компьютер реализует алгоритм Э. Кокейна и Д. Хьюджилла из Университета Виктории. Алгоритм гарантирует кратчайшую сеть. Задача с 29 точками на сегодня близка к пределу вычислительных возможностей. |
Задачу Штейнера невозможно решить, просто рисуя линии между заданными точками. Для решения необходимо добавить новые точки, называемые точками Штейнера и служащие в качестве узлов искомой кратчайшей сети. Чтобы определить количество и расположение точек Штейнера, математики и программисты разработали специальные алгоритмы. Однако даже лучшие из этих алгоритмов, выполняющиеся на самых быстродействующих компьютерах, не в состоянии дать решение для большого множества заданных точек за реально приемлемое время. Более того, задача Штейнера принадлежит к классу задач, для которых, по мнению многих современных исследователей, эффективные алгоритмы, по-видимому, так никогда и не будут найдены. Поэтому компьютерная компания Cavalieri должна быть реабилитирована.
В то же время фирма Cavalieri могла бы разработать практически полезную программу, которая находила бы сеть, несколько более длинную по сравнению с кратчайшей. Приближённые методы решения довольно часто применяются в различных приложениях задачи поиска кратчайших сетей. Среди них — конструирование интегральных электронных схем, построение эволюционного дерева для группы биологических видов и минимизация расхода материалов на создание сетей телефонных линий, трубопроводов и шоссейных дорог.
В общей форме задача Штейнера была впервые сформулирована в статье Милоша Кёсслера и Войцеха Ярника, опубликованной в 1934 году, однако сама эта проблема не приобрела широкой известности вплоть до 1941 года, когда Рихард Курант и Герберт Е. Роббинс включили её в свою книгу «Что такое математика?». Курант и Роббинс связали эту задачу с исследованиями Якоба Штейнера, немецкого математика XIX столетия, работавшего в Берлинском университете. Работа Штейнера была посвящена поиску одной точки, сумма расстояний от которой до всех точек заданного множества была бы минимальной. Однако ещё в 1640 году впервые была поставлена задача, являющаяся частным случаем обеих описанных задач — той, над которой работал Штейнер, и той, которая носит его имя: найти точку P, сумма расстояний от которой до каждой из трёх заданных точек минимальна. Эванджелиста Торричелли и Бонавентура Кавальери независимо друг от друга решили эту задачу. Торричелли и Кавальери доказали, чту суммарное расстояние минимально, когда все сопряжённые углы в точке P больше или равны 120°.
Зная, что углы с вершинами в точке P должны быть не меньше 120°, Торричелли и Кавальери придумали процедуру геометрического построения для нахождения точки P (см. рис.).
|
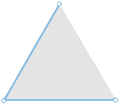
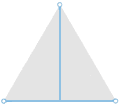
Кратчайшая сеть для трёх точек A, B и C. На самой длинной стороне треугольника ABC строится равносторонний треугольник ACX (зелёный цвет), и вокруг него описывается окружность (жёлтый цвет). На пересечении её с отрезком BX находится точка P, называемая точкой Штейнера. Отрезки AP, BP и CP образуют три сопряжённых угла по 120° и кратчайшую сеть, причём их суммарная длина равна BX. |
Нужно провести отрезки прямых, соединяющие исходные точки (назовем их A, B и C), с точкой в вершине наибольшего угла (скажем, B). Если угол B больше или равен 120°, то искомая точка P совпадает с точкой B. Другими словами, кратчайшая сеть в данном случае представляет собой просто два отрезка прямых между точками A и B и точками B и C. Если угол в точке B меньше 120°, то точка P должна находиться где-то внутри треугольника. Чтобы найти её, следует построить равносторонний треугольник с основанием на самой большой стороне треугольника ABC, а именно на отрезке AC. Третья вершина равностороннего треугольника (обозначим её X) находится на противоположной стороне от точки B относительно AC. Вокруг построенного равностороннего треугольника описываем окружность и проводим прямую, соединяющую точки B и X. Точка P будет на пересечении этой прямой и окружности. Соединив точки A, B и C с точкой P, мы получаем три угла, в точности равные 120° каждый, и искомую кратчайшую сеть. Более того, длина отрезка BX оказывается равной длине кратчайшей сети. В дальнейшем в нашей статье мы будем называть точку X замещающей точкой, поскольку замена точек A и C одной точкой X не изменяет длину сети.
Задача с тремя точками и задача Штейнера для многих точек имеют много общих свойств. Их решения, имеющие вид дерева, характерны тем, что при удалении любого отрезка из кратчайшей сети мы должны будем исключить одну из заданных точек. Другими словами, мы не можем пройти по сети из какой-либо заданной точки и вернуться в неё, без того чтобы не пройти те или иные отрезки повторно. По этой причине графические решения задачи с тремя точками и задачи со многими точками называются деревьями Штейнера. Отрезки прямых называются рёбрами, а точки, роль которых аналогична точке P и которые нужно добавить для построения дерева, называются точками Штейнера.
Задача Штейнера для трёх точек даёт также некоторую информацию о геометрии кратчайших деревьев Штейнера. Во-первых, каждый угол равен 120° или больше, а это означает, что каждая точка соединяется с остальным деревом не более чем тремя рёбрами. Во-вторых, в каждой точке Штейнера сходятся ровно три ребра, образуя друг с другом углы, в точности равные 120°. В-третьих, число рёбер дерева всегда на единицу меньше суммарного числа заданных исходных точек и точек Штейнера. И наконец, последнее свойство: поскольку в каждой точке Штейнера сходятся ровно три ребра и по крайней мере одно ребро должно касаться каждой из заданного множества точек, максимальное число точек Штейнера для любой задачи на две меньше, чем число заданных исходных точек.
|
|
|
|
|
|||
8 |
|
7,464... |
|
6,928... |
|||
d |
|
e |
|
f |
|||
|
|
|
|
|
|||
g |
|
h |
|
i |
|||
|
|
|
|
|
Задача поиска сети для точек, расположенных в вершинах равностороннего треугольника, прямоугольника и «лестницы» имеет различные решения. В случаях a, d и g точки соединяются без дополнительных промежуточных точек и такое решение называется минимальным остовным деревом. Деревья Штейнера, полученные путём добавления узловых точек, показаны для случаев b, c, e, f, h и i. Только c, f и i являются кратчайшими деревьями Штейнера, или кратчайшими сетями. Числа под каждым решением указывают примерную суммарную длину отрезков сети. |
При одном и том же количестве и расположении исходных точек можно построить много различных деревьев Штейнера, удовлетворяющих перечисленным выше условиям. Некоторые из этих деревьев, называемые локально минимальными решениями, невозможно сократить за счёт мелкомасштабных изменений, таких как небольшое перемещение ребра или расщепление точки Штейнера. Однако не всякое локально минимальное дерево Штейнера даёт кратчайшее из возможных решений задачи. Для того чтобы преобразовать сеть в кратчайшее дерево, называемое глобально минимальным деревом Штейнера, могут потребоваться крупномасштабные перемещения точек Штейнера.
Рассмотрим для примера множество исходных точек, образующих четыре угла прямоугольника, размерами три метра на четыре. Решения содержат две точки Штейнера, которые можно расположить двумя различными способами. При каждом расположении мы получаем дерево Штейнера, причём в каждой точке Штейнера сходятся по три ребра под углом 120°. Если точки Штейнера расположить на линии, параллельной поперечной стороне прямоугольника, то получается локально минимальное дерево Штейнера длиной 9,9 м. Если расположить точки Штейнера на линии, параллельной продольной стороне прямоугольника, то получится глобально минимальное дерево длиной 9,2 м.
Действуя методом полного перебора, можно найти кратчайшую сеть путём построения всех возможных локально минимальных деревьев Штейнера, вычислением их длины и выбором кратчайшего. Но поскольку расположение точек Штейнера неоднозначно, возникает сомнение в том, что вычислить все локально минимальные деревья Штейнера можно за конечное время. З. Мелзак из Университета Британской Колумбии сумел преодолеть это затруднение и составил первый алгоритм для решения задачи Штейнера.
В алгоритме Мелзака рассматриваются многие возможные соединения между заданными точками и многие возможные расположения точек Штейнера. Алгоритм можно условно разбить на две части. В первой его части множество исходных точек просто подразделяется на всевозможные подмножества. Во второй части для каждого такого подмножества создается ряд возможных деревьев Штейнера с использованием построения, аналогичного тому, которое мы применили к задаче с тремя точками.
Так же как и для трёх точек, вместо двух исходных точек можно подставить одну заменяющую их точку, не изменяя результата (длины сети) решения. Однако в общем случае алгоритм должен угадать, какую пару следует заменить, и поэтому он перебирает все возможные пары. Более того, заменяющая точка может размещаться по любую сторону от прямой, соединяющей две заменяемые точки, поскольку равносторонний треугольник, используемый при построении, может быть ориентирован в одном из двух направлений. После того как одна из точек в подмножестве заменена одной из двух возможных заменяющих точек, на каждом последующем шаге алгоритма замещаются либо две другие исходные точки, либо одна исходная и одна замещающая, либо две замещающие другой замещающей точкой; и так до тех пор, пока всё подмножество не будет сведено к трём точкам.
Как только для этих трёх точек найдена точка Штейнера, алгоритм начинает работать в обратном направлении, пытаясь определить точку Штейнера, соответствующую каждой замещающей точке (см. рис.).
|
Алгоритм Мелзака разбивает задачу поиска кратчайшей сети на подзадачи. Точка A подходит для разбиения задачи на подзадачи из 3 и 5 точек. Чтобы построить возможные деревья Штейнера для 5 точек, пару точек (например, B и C) можно заменить одной (здесь X), построив равносторонний треугольник с основанием BC. Теперь задача сведена к 4 точкам: X, D, G и A. Пару точек опять можно заменить — сначала D и X на Y, а потом G и A на Z. Вокруг каждого из полученных равносторонних треугольников (XDY, AGZ и BCX) описываем окружности. Точки Q и R, в которых прямая YZ пересекает две окружности, — это точки Штейнера, а пересечение прямой XQ с третьей окружностью определяет точку Штейнера P. Поскольку невозможно заранее предугадать наилучшее разбиение на подзадачи и группировки на пары, необходимо рассмотреть все варианты, чтобы найти кратчайшее дерево. |
Попытка может окончиться неудачей, поскольку на расположение точек Штейнера накладываются противоречащие друг другу ограничения. Однако успешная попытка приводит к возникновению дерева Штейнера, соединяющего каждую исходную точку подмножества с деревом одним ребром. Рассмотрев, таким образом, все замещающие последовательности, алгоритм выбирает кратчайшее из этих деревьев Штейнера для подмножества. Комбинируя между собой всевозможными способами кратчайшие деревья Штейнера для подмножеств так, чтобы охватить исходное множество точек, можно построить всевозможные локально минимальные деревья Штейнера и определить геометрию кратчайшей сети.
Алгоритм Мелзака может потребовать колоссального времени даже для небольших задач, поскольку в нём рассматривается очень много вариантов. Например, задача для 10 точек может быть распределена на 512 подмножеств исходных точек. И хотя двухточечные подмножества не требуют большого объёма работы, каждое из 45 подмножеств с восемью точками имеет два миллиона замещающих последовательностей. Кроме того, существуют ещё более 18 000 способов объединить эти подмножества в деревья.
Разумеется, исследователи нашли более эффективные пути организации вычислений и сумели повысить быстродействие алгоритма. Вместо того чтобы рассматривать геометрию задачи, они фокусируют внимание на возможных конфигурациях соединений в сети, т.е. на её топологии. Топология указывает, какие точки соединены друг с другом, а не действительные расположения точек Штейнера. Приняв определённую топологию, можно найти соответствующую замещающую цепочку относительно быстро. При такой организации процесса скорость вычисления кратчайших деревьев Штейнера для подмножеств немного возрастает. Например, для подмножества из 8 точек алгоритм должен рассмотреть лишь около 10 000 различных топологий вместо двух миллионов различных последовательностей замещения.
Так как количество возможных топологий быстро возрастает с размером подмножества, задачи Штейнера могут стать менее трудоёмкими лишь в том случае, если требуется рассматривать только очень небольшие подмножества исходного множества точек. Эксперименты, проведённые с алгоритмом Мелзака, показали, что кратчайшая сеть для числа случайных точек больше 6 обычно может быть разбита на кратчайшие сети для меньших наборов точек. Однако, рассмотрев специальные конфигурации точек, называемые лестницами, Ф. Чанг из фирмы Bell Communications Research совместно с одним из авторов настоящей статьи (Грэмом) показал, что существуют бесконечно большие множества точек, для которых кратчайшее дерево Штейнера невозможно расчленить. Лестница — это конфигурация, в которой исходные точки расположены равномерно вдоль двух параллельных линий. Для этой весьма частной задачи Штейнера было найдено общее решение. Оно показало, что число точек Штейнера в кратчайшем дереве Штейнера для лестницы с нечётным количеством «ступенек» максимально: оно равно числу исходных точек минус 2. Такое дерево Штейнера невозможно расчленить, потому что для каждой точки Штейнера нужно одновременно учитывать все исходные точки. Следовательно, не всегда можно сократить размер подмножеств, рассматриваемых алгоритмом Мелзака.
Некоторым исследователям удалось улучшить эффективность алгоритмов по сравнению с алгоритмом Мелзака за счёт применения более тонких способов, позволяющих уменьшить объём вычислений (см. рис.).
|
Методы усечения повышают эффективность алгоритмов поиска кратчайших сетей. Один из приёмов усечения, или исключения, возможных сетей (изобретённый Кокейном) заключается в том, чтобы рассмотреть порядок, в котором резиновое кольцо (красный цвет), натянутое вокруг заданного множества точек, касается их. Резинка касается всех точек, за исключением C и H, но C можно включить в последовательность, поскольку угол, образуемый точкой C с двумя соседними точками, находящимися в контакте с резинкой, не меньше 120°. Тогда порядок точек будет ABCDEFG. Непрерывный путь (чёрный цвет), проходящий вдоль возможной сети (синий цвет), касается точек в порядке ACBDEFHG. Поскольку B и C здесь переставлены местами по отношению к последовательности, образованной резинкой, эту сеть можно исключить из рассмотрения. |
В их алгоритмах производится усечение вычислительной процедуры, т.е. прекращаются те ветви вычисления, которые заведомо должны привести к сравнительно длинным сетям. Новые методы усечения действительно значительно сокращают объём вычислений. Программы, основанные на алгоритме Мелзака, как, скажем, программа Э. Кокейна из Университета Виктории, написанная в 1969 году, могли решить любую задачу для 9 точек и некоторые задачи для 12 точек приблизительно за полчаса. Программа же, недавно написанная Кокейном и его коллегой из Университета Виктории Д. Хьюджиллом, использует мощный метод усечения, изобретённый Р. Винтером из Копенгагенского университета. Эта программа смогла решить все задачи для 17 точек и большинство случайно сгенерированных задач для 30 точек всего за несколько минут. Метод усечения Винтера оказался настолько удачным, что благодаря устранению большинства возможных топологий, основной объём вычислительной работы связан с комбинированием решений, полученных для отдельных подмножеств.
Однако для всех этих программ время решения задачи может сильно зависеть от геометрии и от количества точек. Более того, время вычислений даже для самых изощрённых алгоритмов растёт по экспоненциальному закону с ростом числа точек, и задачи Штейнера для 100 точек остаются практически неразрешимыми. Будет ли когда-нибудь найден эффективный алгоритм, позволяющий решать большие задачи Штейнера?
Прогресс, достигнутый в теории вычислительной математики, убедил большинство исследователей, что существующие алгоритмы решения задачи Штейнера практически невозможно улучшить. В этой теории каждой задаче сопоставляется определённый размер. Для каждого конкретного случая задачи Штейнера таким естественным размером является число заданных исходных точек. Затем рассматривается количество элементарных компьютерных операций — таких как сложение, вычитание и умножение, — которое может потребоваться алгоритму для решения какого-то частного случая задачи определённого размера. Поскольку различные частные случаи одного и того же размера могут потребовать различного количества операций, следует рассматривать максимальное количество операций как функцию размера задачи. Если число операций растет с размером задачи (n) пропорционально некоторой степени размера, например, как в выражениях n2, 5n или 6n + n10, то процедура решения называется алгоритмом с полиномиальным временем, или просто полиномиальным алгоритмом. Такие алгоритмы считаются эффективными, по крайней мере в теоретическом смысле. Если же количество операций возрастает экспоненциально с размером задачи, как, например, в случаях 2n, 5n или 3n2·4n, процедура решения называется алгоритмом с экспоненциальным временем или просто экспоненциальным алгоритмом.
Хотя для очень маленьких задач и полиномиальные, и экспоненциальные алгоритмы достаточно практичны, для больших задач время решения у экспоненциальных алгоритмов настолько велико, что практически они оказываются безнадёжными (см. H. Lewis, C. Papadimitriou. The Efficiency of Algorithms, Scientific American, January, 1978). Для достаточно больших задач полиномиальный алгоритм, выполняющийся даже на самой медленной машине, даёт решение всё-таки значительно быстрее, чем экспоненциальный алгоритм, выполняющийся на суперкомпьютере.
Хотя для задачи Штейнера были найдены экспоненциальные алгоритмы (например, алгоритм Мелзака), ни одного полиномиального алгоритма найти для неё не удалось. И шансы на то, что эффективный алгоритм будет когда-нибудь найден, очень малы. В 1971 году С. Кук из Университета в Торонто доказал, что если будет найден полиномиальный алгоритм для любой задачи, принадлежащей классу труднорешаемых задач, называемых NP-полными, то этим же алгоритмом можно будет воспользоваться для эффективного решения широкого класса труднорешаемых задач, включая класс NP-полных. Позже один из авторов настоящей статьи (Грэм), работая совместно с М. Гэри и Д. жонсоном из AT&T Bell Laboratories, доказал, что задача Штейнера относится к классу NP-полных. Поскольку до сегодняшнего дня все NP-полные задачи оказались не по силам тысячам исследователей, то маловероятно, чтобы какая-нибудь NP-полная задача, в том числе и задачи Штейнера, была решена алгоритмом с полиномиальным временем. Однако доказательство того, что NP-полные задачи невозможно решить эффективным способом, остаётся одной из основных теоретических проблем вычислительной математики.
Хотя представляется очень маловероятным, чтобы появился эффективный алгоритм с полиномиальным временем, вычисляющий кратчайшие сети, существуют практичные алгоритмы, отыскивающие несколько более длинные сети. Одним из примеров является в этом смысле алгоритм, решающий задачу минимального остовного дерева, который отыскивает кратчайшую систему прямолинейных отрезков, связывающих данное множество точек без добавления новых. Чтобы решить эту задачу, нужно соединить две точки, ближе всего расположенные друг к другу, и на каждом последующем шаге соединять ближайшую пару точек, которую можно соединить, не образуя замкнутого пути. В конце концов, можно удалить одно ребро из замкнутого пути, и заданные исходные точки останутся всё же связанными остающимися рёбрами.
Е. Гилберт и X. Поллак высказали предположение о том, что отношение длины кратчайшего дерева Штейнера к длине минимального остовного дерева равно, самое меньшее, v3/2, т.е. дерево Штейнера не более чем на 13,4% короче минимального остовного дерева. Это отношение v3/2 возникает в простом примере, когда три исходные точки являются вершинами равностороннего треугольника. Хотя это предположение остаётся недоказанным, Чанг и один из авторов данной статьи (Грэм) показали, что дерево Штейнера короче минимального остовного дерева не более чем на 17,6%.
Минимальные остовные деревья можно часто укоротить на 3 или 4% путём тщательного выбора дополнительных точек Штейнера и небольшой переделки дерева. Одному из авторов (Берну) удалось показать, что этот неточный алгоритм до какой-то степени оправдан в теоретическом смысле, поскольку в среднем длина модифицированного дерева будет немного меньше средней длины минимального остовного дерева.
Задачи отыскания минимального остовного дерева и кратчайшей сети решались в применении к планированию топологии телефонных сетей, трубопроводов и шоссейных дорог. Решения, приближённые или точные, помогают спланировать геометрию сети и подсчитать необходимые количества материалов. В более сложных формулировках задачи Штейнера можно учитывать такие факторы, как необходимость избежания определённых географических свойств местности, а также отыскивать кратчайшие соединения между узлами уже существующих сетей.
Возможно, наиболее важным практическим применением задачи Штейнера является конструирование интегральных электронных схем. Более короткая сеть проводящих линий на интегральной схеме требует меньшего времени зарядки-разрядки по сравнению с более длинной сетью и повышает, таким образом, быстродействие схемы. Однако задача отыскания кратчайшей сети на интегральной схеме имеет другую геометрию, так как проводники на ней обычно проходят лишь в двух направлениях — горизонтальном и вертикальном.
|
Разновидности задачи о кратчайшей сети применялись при конструировании электронных интегральных схем, с тем чтобы повысить их быстродействие. Кратчайшая сеть из вертикальных и горизонтальных проводников, связывающих множество выводов, выделена красным цветом. Здесь показаны также проводники и выводы в более глубоких слоях схемы. |
Такая задача, получившая название прямоугольной задачи Штейнера, была впервые изучена в 1965 году Морисом Хэнаном из Исследовательского центра им. Томаса Уотсона корпорации IBM в Йорктаун-Хейтсе (шт. Нью-Йорк). Как и в классической задаче Штейнера, решение для прямоугольной её версии также содержит точки Штейнера и исходные точки, но рёбра встречаются в них под углом либо 90°, либо 180°. Хотя точки Штейнера могут, казалось бы, лежать повсеместно в прямоугольной задаче, так же как и в классической задаче Штейнера, Хэнан показал, что в кратчайшей прямоугольной сети на расположение точек Штейнера можно наложить определённые ограничения. Через каждую исходную точку проводятся горизонтальная и вертикальная прямые, и каждое пересечение двух линий даёт возможное положение точки Штейнера. Чтобы найти кратчайшую сеть, алгоритм может рассмотреть все подмножества возможных точек Штейнера. Однако по мере того, как число исходных точек возрастает, время решения для каждого алгоритма, осуществляющего полный перебор вариантов, растёт экспоненциально. Более тонкие, но всё же экспоненциальные алгоритмы способны решать прямоугольные задачи Штейнера размером порядка 40 точек.
Прямоугольная версия задачи поиска минимального остовного дерева может быть эффективно решена алгоритмом, выбирающим на каждом шаге кратчайшее соединение, если это соединение не образует замкнутого пути. Ф. Хванг из фирмы Bell Laboratories показал, что прямоугольное дерево Штейнера не бывает короче прямоугольного остовного дерева более чем на одну треть.
Наиболее удивительное применение задача Штейнера нашла в биологии, в одной из областей, изучающей происхождение видов. Д. Сэнкофф из Монреальского университета и ряд других исследователей сформулировали одну из версий задачи Штейнера для того, чтобы вычислять наиболее вероятные филогенетические деревья. Учёные сначала изолируют какой-то определённый белок, общий для организмов, которые они намереваются классифицировать. Затем для каждого организма они определяют последовательность аминокислот, составляющих этот белок, и устанавливают точку в позиции, определяемой числом различий между белком соответствующего организма и белком других организмов. Организмы с похожими последовательностями аминокислот определяются, таким образом, как близкие, а организмы с непохожими последовательностями — как далёкие. В кратчайшей сети для этого абстрактного множества исходных точек точки Штейнера соответствуют наиболее вероятным предкам, а рёбра представляют связь между данным организмом и предком, обладающую наименьшим числом мутаций. Однако, поскольку филогенетическая задача Штейнера не легче других задач подобного рода, эта задача — за исключением случаев с небольшим числом организмов — послужила скорее в качестве мысленного эксперимента, нежели практического инструмента исследований.
Хотя за последние годы наши познания в области алгоритмов значительно расширились, задача поиска кратчайшей сети остаётся всё такой же неприступной. Несмотря на то что формулировка этой задачи очень проста, её решения трудно поддаются анализу. Крошечное изменение геометрии задачи, кажущееся несущественным, может коренным образом изменить кратчайшую сеть, являющуюся её решением. Такая чувствительность к исходным данным делает даже периферийные вопросы, касающиеся кратчайших сетей, весьма не простыми. Задача поиска кратчайшей сети будет ещё долгие годы привлекать наше воображение.
Литература
1. |
E. N. Gilbert and H. О. Pollak. Steiner Minimal Trees. In: SIAM Journal on Applied Mathematics, 1968, v. 16, No 1, pp. 1–29. |
2. |
Z. A. Melzak. Companion to Concrete Mathematics. John Wiley & Sons, Inc., 1973. |
3. |
Pawel Winter. An Algorithm for the Steiner Problem in the Euclidean Plane. In: Networks, 1985, v. 15, No 3, pp. 323–345. |
4. |
Pawel Winter. Steiner Problem in Networks: A Survey. In: Networks, 1987, v. 17, No 2, pp. 129–167. |
5. |
М. Гэри, Д. Джонсон. Вычислительные машины и труднорешаемые задачи. — Перев. с англ. М.: Мир, 1982. |
Сопряжённые числа
Вагутен Н.
Читателю, вероятно, известны на первый взгляд трудные геометрические задачи, которые мгновенно решаются, если заменить одну данную точку другой, симметричной ей относительно какой-то прямой. Соображения симметрии очень важны и в алгебре.
В этой статье мы рассмотрим ряд ситуаций, в которых число вида a + b√d полезно заменить сопряжённым a – b√d. Мы увидим, как этот простой приём — замена знака перед радикалом — помогает в решении разнообразных задач алгебры и анализа — от нехитрых оценок и преобразований до трудных олимпиадных задач и замысловатых придумок составителей конкурсных экзаменов.
Большинство наших примеров может служить первым знакомством с глубокими математическими теориями (кое-где мы указываем статьи и книги для продолжения знакомства). Среди задач, включённых в статью, две — из Задачника «Кванта» и несколько — из писем читателей, уже испытавших удовольствие от трюков с радикалами и желающих поделиться им с другими.
Пары сопряжённых чисел появляются вполне естественным образом, когда мы решаем квадратное уравнение, а корень из дискриминанта не извлекается: скажем, уравнение λ2 – λ – 1 = 0 имеет пару «сопряжённых» корней:
λ1 = |
1 – √5 2 |
и |
λ2 = |
1 + √5 2 |
. |
К этому мы ещё вернёмся, а начнём с примеров другого рода: займёмся «перебросками»...
...Из числителя в знаменатель
(и обратно)
Если в книжке указан ответ к задаче (3 + √7)/2, а у вас получилось 1/(3 – √7) — не спешите искать ошибку в решении: ответ правильный — эти числа равны, потому что
(3 + √7)(3 – √7) = 32 – 7 = 2.
Вот несколько характерных примеров, где полезно перенести «иррациональность» из числителя в знаменатель или наоборот.
1. Найти сумму
1 1 + √2 |
+ |
1 √2 + √3 |
+ ... + |
1 √99 + √100 |
. |
Эта сумма мгновенно «сворачивается», если переписать её так:
(√2 – 1) + (√3 – √2) + ... + (√100 – √99) = –1 + 10 = 9.
По выражению из статьи [1] «остаются крайние» (см. также [5]).
2. Доказать, что для любых натуральных m и n
|
(1) |
где α = √3 + √2.
Подобный факт мы использовали недавно при решении трудной задачи М514 ([2]).
В самом деле, всегда
|
(2) |
поскольку число |m2 – 2n2| — целое и отлично от 0 (равенство m2 = 2n2 невозможно — подумайте, почему!). Если бы выполнялось неравенство, противоположное (1), то должно было бы быть m < n√2 + 1/αn и
|
(3) |
Но из (2) и (3) следует (1). Значит, наше предположение неверно, то есть (1) выполнено.
Неравенство (1) показывает, что число √2 сравнительно плохо приближается дробями с небольшими знаменателями; аналогичное неравенство (только с другим коэффициентом α) выполнено не только для √2, но и для любой «квадратичной иррациональности». Разумеется, (1) выполнено и при всех α > √3 + √2, но константа √3 + √2 здесь не наименьшая из возможных. Вопросы о приближениях квадратичных иррациональностсй рациональными числами — далеко продвинутая и важная для приложений область теории чисел ([3], [4]); с приближениями числа √2 мы ещё встретимся ниже (см. упражнение 4).
[Если при решении этой задачи рассмотреть отдельно случаи n=1 и n≠1, то можно показать, что
|
m n |
– √2 |
|
≥ |
1 πn2 |
. |
Оно лишь немного сильнее, чем неравенство (1), поскольку
1 π |
= 0,3183... > 0,3178... = |
1 √3 + √2 |
, |
зато выглядит гораздо эффектнее.
Помню, как в мою бытность студентом, на лекциях по алгебре наш профессор говорил: «Корень из трёх — это, примерно, 1,73; корень из двух — 1,41. Поэтому их сумма равна... (следовала пауза, необходимая для сложения этих чисел "в столбик") 3,14. А это есть?..» (он поворачивался к аудитории и сразу несколько человек говорили "пи") «Ну, вот», — с удовлетворением заключал профессор, выписывая окончательное "равенство": √3 + √2 = π. :) — E.G.A.]
3. Найдите предел последовательности an = (√n² + 1 – n)n.
Преобразуем an так:
(√n² + 1 – n)n = |
n √n² + 1 + n |
= |
1 1 + √1 + 1/n² |
. |
Теперь ясно, что an возрастает и стремится к пределу 1/2.
В противоположность предыдущему примеру здесь мы имеем дело с хорошим приближением: √n² + 1 – n < 1/2n.
4 (M532). Даны две последовательности an = √n+1 + √n и bn = √4n+2. Докажите, что
а) [an] = [bn],
б) 0 < bn – an < 1/16n√n.
В разности bn – an появляется «тройная иррациональность»; к таким иррациональностям мы ещё вернёмся (см. задачу 8), но пока мы будем рассматривать √n+1 + √n = an как одно целое. Заметим, что величина an2=2n+1+2√n(n+1), очевидно, заключена между 4n+1 и 4n+2=bn2, поскольку n < √n(n+1) < n+1. Итак, мы уже получили an < bn — левое неравенство в б). Кроме того, число bn2 = 4n+2, дающее при делении на 4 в остатке 2, не может быть полным квадратом (проверьте!), поэтому квадрат целого числа [bn] не больше 4n+1; из неравенств [bn] ≤ √4n+1 < an < bn вытекает а). Теперь осталось оценить разность bn – an сверху. Посмотрите, как здесь дважды работает переброска «сопряжённого» числа в знаменатель:
√4n+2 – √n – √n+1 = |
2n + 1 – 2√n(n + 1) √4n + 2 + √n + √n + 1 |
= |
= |
1 (√4n + 2 + √n + √n + 1)(2n + 1 + 2√n(n + 1) ) |
≤ |
(тут, конечно, нам повезло: разность квадратов (2n + 1)2 – 4n(n + 1) равна 1)
≤ |
1 (2√n + √n + √n)(2n + 2n) |
= |
1 16n√n |
. |
Заметим, что и эта оценка очень точная. Но убедиться в этом (и вообще исследовать поведение функции с многими радикалами) лучше уже не с помощью алгебраических преобразований, а средствами анализа — заменить переменную n на h = 1/n и воспользоваться формулой Тейлора √1 + h = 1 + h/2 – h2/8 + ... (См. [6].)
Заменим плюс на минус
Мы уже говорили о пользе симметрии в геометрических задачах. Своего рода симметрией в алгебре является замена плюса на минус.
Так, если какое-либо выражение от √d равно p + q√d и мы всюду в этом выражении заменим √d на –√d, то естественно ожидать, что новое выражение окажется равным сопряженному числу p – q√d. Мы будем пользоваться таким очевидным частным случаем этого свойства (a и b — рациональны, √d — нет):
(a + b√d)n = p + q√d => (a – b√d)n = p – q√d. |
(4) |
5. Доказать, что уравнение
(x + y√5)4 + (z + t√5)4 = 2 + √5
не имеет решений в рациональных числах x, y, z, t.
Можно, конечно, найти отдельно сумму членов левой части, не содержащих √5 (она должна быть равна 2), и отдельно — коэффициент при √5 (он должен равняться 1). Но что делать с полученной громоздкой системой неясно. Вместо этого воспользуемся (4) и заменим плюс перед √5 на минус!
(x – y√5)4 + (z – t√5)4 = 2 – √5.
Слева стоит неотрицательное число, справа — отрицательное.
6. Доказать, что существует бесконечно много пар (x; y) натуральных чисел, для которых x2 отличается от 2y2 на 1:
| x2 – 2y2 | = 1. |
(5) |
Несколько таких пар с небольшими (x; y) легко найти подбором: это (1; 1), (3; 2), (7; 5), (17; 12), ... (рис. 1). Как продолжить этот набор? Можно ли записать общую формулу для этих решений?
|
Найти ответы на эти вопросы нам поможет число 1 + √2. Закономерность, позволяющая получать всё новые и новые решения (x; y), указана в таблице:
n |
(1 + √2)n |
xn |
yn |
xn2 – 2yn2 |
(1 – √2)n |
1 |
1 + √2 |
1 |
1 |
1 – 2 = –1 |
1 – √2 |
2 |
3 + 2√2 |
3 |
2 |
9 – 8 = 1 |
3 – 2√2 |
3 |
7 + 5√2 |
7 |
5 |
49 – 50 = –1 |
7 – 5√2 |
4 |
17 + 12√2 |
17 |
12 |
289 – 288 = 1 |
17 – 12√2 |
5 |
41 + 29√2 |
41 |
29 |
1681 – 1682 = –1 |
41 – 29√2 |
... |
... |
... |
... |
... |
... |
Какой будет шестая строчка?
Видно, что коэффициенты xn, yn в числе
xn + yn√2 = (1 + √2)n
будут давать нужную пару. Доказать это поможет колонка таблицы из сопряжённых чисел (мы снова применяем (4)):
xn – yn√2 = (1 – √2)n.
Перемножив два последних равенства, получим
x |
2 n |
– 2y |
2 n |
= (–1)n, |
и интересующее нас выражение попеременно равно то 1, то –1. Складывая и вычитая эти же два равенства, мы получим явное выражение для xn и yn:
xn = |
(1 + √2)n + (1 – √2)n 2 |
, |
yn = |
(1 + √2)n – (1 – √2)n 2√2 |
. |
Можно ли в решении этой задачи про целые числа обойтись без иррациональных чисел 1 + √2 и 1 – √2? Теперь, зная ответ, мы можем легко выразить (xn+1; yn+1) через предыдущую пару (xn; yn): из xn+1 + yn+1√2 = (xn + yn√2)(1 + √2) вытекает
xn+1 = xn + 2yn, yn+1 = xn + yn. |
(6) |
До этого рекуррентного соотношения можно было, видимо, догадаться по нескольким первым решениям, а потом проверить, что
| x |
2 n |
– 2y |
2 n |
| = | x |
2 n+1 |
– 2y |
2 n+1 |
| . |
Добавив начальное условие x1 = 1, y1 = 1, отсюда (по индукции) можно было бы заключить, что |xn2 – 2yn2| = 1 для любого n. Далее, выразив обратно (xn; yn): через (xn+1; yn+1), «методом спуска» ([8]) можно доказать, что найденной серией исчерпываются все решения уравнения (5) в натуральных числах (x; y). Подобным же образом решается любое «уравнение Пелля» x2 – dy2 = c (а к уравнениям такого типа сводится любое квадратное уравнение в целых числах x, y), но у исходного уравнения может быть несколько серий решений ([7]).
Рекуррентные соотношения типа (6) возникают не только в теории чисел, но и в разных задачах анализа, теории вероятностей. Вот характерный пример комбинаторной задачи такого типа (она предлагалась на последней международной олимпиаде в Лондоне):
7 (М595). В вершине A правильного восьмиугольника сидит лягушка. Из любой вершины восьмиугольника, кроме вершины E, противоположной A, она может прыгнуть в любую из двух соседних вершин. Попав в E, лягушка останавливается и остаётся там. Найти количество em различных способов, которыми лягушка может попасть из вершины A в E ровно за m прыжков.
Если раскрасить вершины восьмиугольника через одну в чёрный и белый цвет (рис. 2), сразу станет ясно, что e2k–1 = 0 при любом k: цвет вершин при каждом прыжке меняется. Обозначим через an и cn количество способов, которым лягушка может за 2n прыжков, попасть из вершины A, соответственно, в вершину A и в одну из вершин C (из соображений симметрии ясно, что в каждую из вершин, обозначенных на рисунке буквой C, можно попасть одним и тем же числом способов). Как легко проверить (см. рис.2а,б,в,г),
a1 = 2, c1 = 1;
|
(7) |
А интересующее нас число e2n равно, очевидно, 2cn–1 (рис. 2д).
|
|
|
|
|
Рис. 2. а) |
Из A в C за два прыжка можно попасть только одним способом: c1 = 1. |
б) |
Из A в A за два прыжка можно попасть двумя способами: a1 = 2. |
в) |
В A можно попасть из C двумя способами и из A двумя способами: an+1 = 2an + 2cn. |
г) |
В C можно попасть из A одним способом и из C — двумя: cn+1 = an + 2cn. |
д) |
В E можно попасть из C двумя способами: e2n = 2cn–1. |
Как же найти явную формулу для an и cn? Запишем наше рекуррентное соотношение (7) так:
an+1 + cn+1√2 = (an + cn√2)(2 + √2) |
(8) |
и — как вы уже, конечно, догадались — ещё так:
an+1 – cn+1√2 = (an – cn√2)(2 – √2). |
(9) |
Отсюда по индукции, пользуясь (7), получаем:
an + cn√2 = (2 + √2)n–1 (a1 + c1√2) = (2 + √2)n, |
an – cn√2 = (2 – √2)n–1 (a1 – c1√2) = (2 – √2)n. |
Поэтому
cn = |
(2 + √2)n – (2 – √2)n 2√2 |
, |
а так как e2n = 2cn–1, получаем окончательно
e2n = |
(2 + √2)n–1 – (2 – √2)n–1 √2 |
, e2n–1 = 0. |
Задача решена. Неясно только, как в этой задаче (и в предыдущей задаче 6) можно было додуматься до формул, содержащих ±√2, — ведь в задаче речь идёт о целых числах! (Для участников олимпиады и читателей «Кванта» задача 7 была облегчена тем, что в формулировке указывался ответ — «Квант», 1979, № 11, М595).
Однако «сопряжённые числа» возникли бы совершенно автоматически, если бы мы владели началами линейной алгебры (см. [12]), и применили стандартные правила этой науки к решению уравнений (7). Эти правила предлагают сначала выяснить, какие геометрические прогрессии (an = a0λn, cn = c0λn) удовлетворяют данному рекуррентному соотношению. Значения, для которых такие прогрессии существуют, — они называются характеристическими значениями или собственными числами — определяются из некоторого уравнения (оно тоже называется характеристическим). Для (7) характеристическое уравнение имеет вид λ2 – 4λ + 2 = 0, его корни — как раз 2 + √2 и 2 – √2. Зная эти корни, любое решение рекуррентного соотношения мы можем получить как «линейную комбинацию» соответствующих геометрических прогрессий ([11]). «Начальное условие» (в нашем случае a1 = 2, c1 = 1) определяет нужное нам решение однозначно.
Неудивительно, что даже самые простые рекуррентные целочисленные последовательности, для которых характеристическое уравнение — квадратное с целыми коэффициентами (примеры — те же (6) и (7) или последовательность Фибоначчи 1, 1, 2, 3, 5, 8, ..., Fn+1 = Fn + Fn–1; см. [9], [10]), выражаются, как функции номера, с помощью «сопряжённых» квадратичных иррациональностей.
Заметим, что большее характеристическое число определяет скорость роста последовательности: при больши́х n в задаче 7
en (2 + √2)n/√2.
Можно сказать это ещё так:
|
en+1 en |
= 2 + √2. |
Для задачи 6 аналогичное наблюдение:
|
xn yn |
= √2. |
Интересное продолжение этого факта мы увидим в следующей задаче с бо́льшим числом «сопряжённых» иррациональностей.
Поочерёдно меняем все знаки
8 (М520). Пусть
(1 + √2 + √3)n = qn + rn√2 + sn√3 + tn√6,
где qn, rn, sn и tn — целые числа. Найти пределы
|
rn qn |
, |
|
sn qn |
, |
|
tn qn |
. |
Конечно, мы здесь можем выразить (qn+1; rn+1; sn+1; tn+1) через (qn; rn; sn; tn), пользуясь тем, что
qn+1 + rn+1√2 + sn+1√3 + tn+1√6 = (1 + √2 + √3)(qn + rn√2 + sn√3 + tn√6),
но, наученные опытом, мы уже знаем, что более простые формулы получаются не для самих чисел qn, rn, sn, tn, a для некоторых их комбинаций. Одну такую комбинацию мы уже знаем: это
qn + rn√2 + sn√3 + tn√6 = (1 + √2 + √3)n.
Нетрудно сообразить, каковы будут другие. Рассмотрим вместе с данным числом
λ1 = 1 + √2 + √3,
ещё три «сопряжённых»:
λ2 = 1 – √2 + √3,
λ3 = 1 + √2 – √3,
λ4 = 1 – √2 – √3.
Тогда
qn – rn√2 + sn√3 – tn√6 = λ2n,
qn + rn√2 – sn√3 – tn√6 = λ3n,
qn – rn√2 – sn√3 + tn√6 = λ4n.
Мы можем выразить qn, rn, sn, tn через λ1, λ2, λ3, λ4:
qn = |
λ1n + λ2n + λ3n + λ4n 4 |
, |
|
sn = |
λ1n + λ2n – λ3n – λ4n 4√3 |
, |
rn = |
λ1n – λ2n + λ3n – λ4n 4√2 |
, |
|
tn = |
λ1n – λ2n – λ3n + λ4n 4√6 |
. |
Теперь заметим, что λ1 > |λ2|, λ1 > |λ3|, λ1 > |λ4|. Поэтому
|
rn qn |
= |
|
1 – (λ2/λ1)n + (λ3/λ1)n – (λ4/λ1)n 1 + (λ2/λ1)n + (λ3/λ1)n + (λ4/λ1)n |
· |
1 √2 |
= |
1 √2 |
. |
Аналогично найдём, что
|
sn qn |
= |
1 √3 |
и |
|
tn qn |
= |
1 √6 |
. |
Мы говорили выше, что сопряжённые числа a ± b√d возникают часто как корни квадратного уравнения с целыми коэффициентами. В связи с последней задачей возникает такое желание:
9. Написать уравнение с целыми коэффициентами, один из корней которого равен 1 + √2 + √3.
Возникает подозрение, что вместе с этим числом λ1 уравнению с целыми коэффициентами удовлетворяют и сопряжённые, которые в решении предыдущей задачи мы обозначили λ2, λ3, λ4. Нужное уравнение можно записать так:
(x – λ1)(x – λ2)(x – λ3)(x – λ4) = 0;
то есть
(x – 1 – √2 – √3)(x – 1 + √2 – √3)× (x – 1 – √2 + √3)(x – 1 + √2 + √3) = 0;
после преобразований получаем
((x – 1)2 – 5 – 2√6)·((x – 1)2 – 5 + 2√6) = 0, (x2 – 2x – 4)2 – 24 = 0, x4 – 4x3 – 4x2 – 16x – 8 = 0.
Именно такое уравнение получилось бы в качестве характеристического, если бы мы применили упомянутую мелким шрифтом в конце предыдущего раздела общую теорию к исследованию линейного преобразования
(qn; rn; sn; tn) → (qn+1; rn+1; sn+1; tn+1)
в предыдущей задаче. Заметим, кроме того, что мы на самом деле получили уравнение наименьшей степени (с целыми коэффициентами) с корнем λ1 = 1 + √2 + √3. Попробуйте это доказать!
Алгебраическое послесловие
Мы разобрали несколько примеров, в которых затрагивались пограничные вопросы алгебры, математического анализа и теории чисел. (Каждому направлению, которое мы наметили, можно было бы посвятить более подробную статью в «Кванте»!) В заключение покажем ещё, как можно смотреть на основных героев статьи — «сопряжённые числа» — с чисто алгебраической точки зрения.
Предположим, что у нас есть множество P чисел (или выражений с буквами, или ещё каких-то элементов), с которыми можно выполнять четыре действия арифметики с соблюдением обычных арифметических правил. Такое множество называется полем; поля образуют, например, рациональные и действительные числа. Если в поле P не разрешимо, скажем, уравнение x2 – d = 0, то можно расширить его, рассматривая элементы вида p + q√d, где p, q P, a √d — новый символ, который при умножении сам на себя дает d, т.е. √d·√d = d, так что
(p + q√d)·(p' + q'√d) = (pp' + qq'd) + (pq' + qp')√d.
При d = –1 расширением поля вещественных чисел получаются комплексные числа.
В новом поле P1 — «квадратичном расширении» поля P — есть интересное отображение λ = p + q√d → λ = p – q√d (своеобразная «алгебраическая симметрия»), называемое сопряжением, с такими свойствами:
Все элементы старого поля P переходят в себя;
Все равенства, содержащие арифметические операции, при этом отображении сохраняются:
λ + μ = λ + μ; λ · μ = λ · μ; |
(10) |
Это отображение является частным случаем так называемых автоморфизмов Галуа расширения P1 поля P.
В задачах 8 и 9 мы видели пример «двукратного» расширения — присоединения √2 и затем √3, — в результате которого получилось поле с бо́льшим количеством автоморфизмов Галуа: кроме тождественного отображения, их уже три
(√2 → –√2, √3 → √3; √2 → √2, √3 → –√3; √2 → –√2, √3 → –√3),
и их «взаимодействие» устроено так же, как во множестве самосовмещений прямоугольника.
Оказывается, к основному полю можно присоединять корни любого алгебраического уравнения. Автоморфизмы возникающего нового поля — предмет одной из красивейших ветвей алгебры XIX–XX века, теории Галуа, которая позволяет, в частности, исследовать вопрос о разрешимости уравнений в радикалах ([13], [14]).
Мы закончим эту статью набором задач, в основном продолжающих уже затронутые темы, но требующих иногда и новых соображений, и обещанным списком литературы.
Упражнения
1. |
Что больше: √1979 + √1980 или √1978 + √1981? |
||||||||||||||||||||||||||||||
2. |
Докажите, что при всех положительных x
|
||||||||||||||||||||||||||||||
3. |
Постройте график функции y = √x² – 1 и докажите, что при | x| ≥ 1
|
||||||||||||||||||||||||||||||
4. |
В формуле √2 = 1 + 1/(√2 + 1) заменим √2, стоящий в знаменателе правой части, по той же формуле:
В этой формуле снова заменим нижний √2 на 1 + 1/(√2 + 1), и т.д. n раз. Если теперь нижний корень заменить на 1 или на 2, мы получим два рациональных числа pn, qn. Докажите, что √2 лежит между ними и lim pn = lim qn = √2. (Не встречались ли мы с этими числами в одной из задач?) |
||||||||||||||||||||||||||||||
5. |
Докажите, что уравнения а) x2 – 3y2 = 1, б) x2 – 3y2 = 2 имеют бесконечное множество решений в целых числах. |
||||||||||||||||||||||||||||||
6. |
Докажите, что функция y = ln (√x² + 1 + x) — нечётная, и постройте её график. |
||||||||||||||||||||||||||||||
7. |
а) Докажите, что для любого натурального n
б) Докажите, что последовательность
убывает и стремится к пределу. |
||||||||||||||||||||||||||||||
8. |
а) Докажите, что последовательность {(2 + √3)n} сходится, и найдите её предел. б) Каковы первые 100 десятичных знаков после запятой в записи числа (√50 + 7)100? |
||||||||||||||||||||||||||||||
9. |
Докажите, что для любого натурального d, не являющегося полным квадратом, найдётся такое α, что для любых m и n
|
||||||||||||||||||||||||||||||
10. |
Докажите, что при любом натуральном n число [(35 + √1157)n/2n] делится на 17, и вообще для любых натуральных k и n число [(2k + 1 + √4k² + 1)n/2n] делится на k. |
||||||||||||||||||||||||||||||
11. |
Докажите, что для любого числа p>2 найдётся такое число β, что для каждого n справедлива формула (в левой части n вложенных радикалов)
|
||||||||||||||||||||||||||||||
12. |
Докажите, что последовательность bm = 1 + 17m2 содержит бесконечно много квадратов целых чисел. |
||||||||||||||||||||||||||||||
13. |
Составьте квадратное уравнение с целыми коэффициентами, один из корней которого (3 + √5)/4. |
||||||||||||||||||||||||||||||
14. |
Составьте уравнение 4-й степени с корнями ±√p ± √q и решите его, как биквадратное уравнение. Сравнивая ответ с данными корнями, докажите популярные формулы для двойных радикалов:
|
||||||||||||||||||||||||||||||
15. |
Освободитесь от иррациональности в знаменателе:
|
||||||||||||||||||||||||||||||
16. |
Лягушка может прыгнуть из каждой вершины правильного треугольника ABC в любую из двух других вершин. Найдите число an способов, которым она может совершить прогулку из n прыжков, начинающуюся и заканчивающуюся в вершине A. Докажите, что существует предел lim an+1/an, и найдите его. |
||||||||||||||||||||||||||||||
Список
дополнительной литературы
1. |
Л. Курляндчик, А. Лисицкий. «Суммы и произведения» («Квант», 1978, № 10). назад к тексту |
2. |
Второе решение задачи М514 («Квант», 1979, № 5, с. 26). назад к тексту |
3. |
Р. Нивен. «Числа рациональные и иррациональные» (М., «Мир», 1966). назад к тексту |
4. |
Д. Фукс, М. Фукс. «О наилучших приближениях» («Квант», 1971, № 6, № 11) и «Рациональные приближения и трансцендентность» («Квант», 1973, № 1). назад к тексту |
5. |
Н. Васильев, В. Гутенмахер. «Прямые и кривые» (М., «Наука», 1978), с. 103–105. назад к тексту |
6. |
А. Н. Маркушевич. «Ряды» (М., «Наука», 1979). назад к тексту |
7. |
Избранные задачи из журнала American Mathematical Monthly (М., «Мир», 1977), с. 560–561. назад к тексту |
8. |
Л. Курляндчик, Г. Розенблюм. «Метод бесконечного спуска» («Квант», 1978, № 1). назад к тексту |
9. |
В. Березин. «Филлотаксис и последовательность Фибоначчи», («Квант», 1979, № 5, с. 53). назад к тексту |
10. |
Н. Н. Воробьев. «Числа Фибоначчи» (Популярные лекции по математике, вып. 6) (М., «Наука», 1978). назад к тексту |
11. |
А. И. Маркушевич. «Возвратные последовательности» (Популярные лекции но математике, вып. 1) (М., «Наука», 1978). назад к тексту |
12. |
Л. И. Головина. «Линейная алгебра и некоторые её приложения» (М., «Наука», 1979). назад к тексту |
13. |
М. М. Постников. «Теория Галуа» (М., Физматгиз, 1963). назад к тексту |
14. |
Ван-дер-Варден. «Алгебра» (М., «Наука», 1976). назад к тексту |



 10
10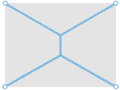 9,928...
9,928... 9,196...
9,196... 10
10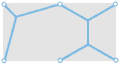 9,327...
9,327...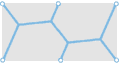 9,250...
9,250...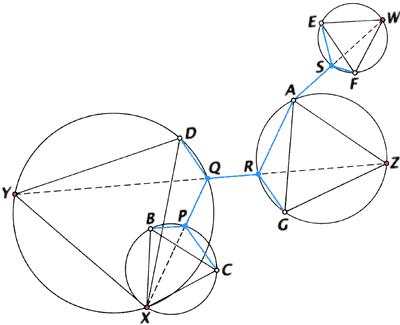

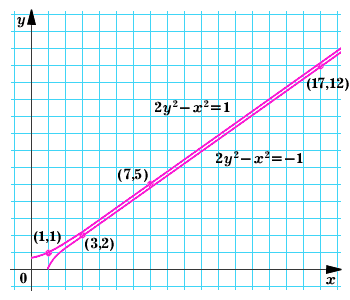 Рис.
1. Проходят ли эти гиперболы
через
бесконечное число узлов клетчатой
бумаги?
Рис.
1. Проходят ли эти гиперболы
через
бесконечное число узлов клетчатой
бумаги?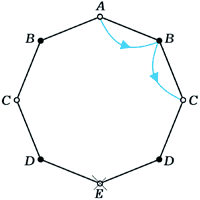 а)
c1
= 1
а)
c1
= 1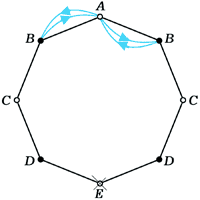 б)
a1
= 2
б)
a1
= 2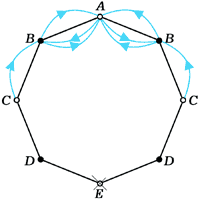 в)
an+1
= 2an
+ 2cn
в)
an+1
= 2an
+ 2cn г)
cn+1
= an
+ 2cn
г)
cn+1
= an
+ 2cn д)
e2n
= 2cn–1
д)
e2n
= 2cn–1