
Применение теоремы Эйлера к некоторым задачам
Бекламов Б. В.
В этой статье мы предлагаем читателям несколько задач, в решении которых центральную роль играет теорема Эйлера. Уделяя основное внимание задачам, мы не доказываем здесь эту теорему, а приводим лишь её формулировку. Доказательство теоремы Эйлера, как и более общие формулировки этой теоремы, можно найти в книгах «Что такое математика?» Куранта и Роббинса и «Наглядная геометрия» Гильберта и Кон-Фоссена.
Прежде чем формулировать теорему Эйлера, договоримся, что линию с концами в двух данных точках мы будем называть дугой, соединяющей эти точки, в том случае, если эту линию можно пройти, не побывав ни в одной из её точек дважды.
Теорема Эйлера. Пусть на плоскости задано m точек и n попарно непересекающихся дуг, каждая из которых соединяет какие-либо две данные точки и не проходит через остальные m–2 точки, и пусть эти дуги делят плоскость на l областей. Если из каждой данной точки в любую из остальных можно попасть, двигаясь по этим дугам, то
m – n + l = 2.
В случае, изображенном на рисунке 1, все условия теоремы Эйлера выполнены, m=12, n=18, l=8 и m–n+l=2. На рисунках 2 и 3 изображены случаи, когда условия этой теоремы не выполняются. Так, на рисунке 2 из точки A1 нельзя попасть в точку A5 и m–n+l=3≠2, а на рисунке 3 линия, соединяющая точки A1 и A2, является самопересекающейся и опять m–n+l=3≠2.
|
|
|
В некоторых задачах совокупность, состоящую из нескольких точек и соединяющих их попарно непересекающихся дуг, мы называем картой; при этом точки из этой совокупности мы называем вершинами, а области, на которые дуги делят плоскость, — странами.
Теперь мы можем перейти к решению задач.
Задача 1. Можно ли десять городов соединить между собой непересекающимися дорогами так, чтобы из каждого города выходило пять дорог, ведущих в пять других городов?
Решение. Предположим, что города можно соединить между собой дорогами так, как указано в задаче. В таком случае, если какие-то два города окажутся не соединенными дорогой непосредственно, то найдётся третий город, который уже будет непосредственно соединён с каждым из них. Изобразив на плоскости города точками, а дороги — дугами, получим, что любые две точки соединены цепочкой дуг. Так как в каждой точке сходятся пять дуг, то общее число дуг равно ½·5·10 = 25. Согласно теореме Эйлера эти дуги делят плоскость на 2 + 25 – 10 = 17 областей. Каждая из этих семнадцати областей ограничена по крайней мере тремя дугами, так как в противном случае нашлись бы два города, непосредственно соединённые по крайней мере двумя дорогами, а это противоречит условию задачи. Следовательно, число дуг не меньше ½·3·17 = 25,5. Таким образом, исходное предположение приводит нас к противоречию, и города нельзя соединить между собой так, как это требуется в задаче.
Задача 2. Три поссорившихся соседа имеют три общих колодца. Можно ли провести непересекающиеся дорожки от каждого дома к каждому колодцу?
Решение. Предположим, что это сделать можно.
Изобразим дома синими, а колодцы — чёрными точками и каждую синюю точку соединим дугой с каждой чёрной точкой так, чтобы девять полученных дуг попарно не пересекались. Тогда всякие две точки, изображающие дома или колодцы, будут соединены цепочкой дуг, и в силу теоремы Эйлера эти девять дуг разделят плоскость на 9–6+2=5 областей. Каждая из пяти областей ограничена по крайней мере четырьмя дугами, так как по условию задачи ни одна из дорожек не должна непосредственно соединять два дома или два колодца. Поэтому число дуг должно быть не меньше ½·5·4 = 10, и, следовательно, наше предположение неверно.
Задача 3. Докажите, что на всякой карте найдётся страна, граничащая не более чем с пятью странами.
Решение. Если число стран на карте не превосходит шести, то утверждение задачи очевидно. Мы докажем, что на карте, имеющей более шести стран, найдутся даже четыре страны, каждая из которых граничит не более чем с пятью странами. Окрасим вершины и дуги исходной карты в чёрный цвет, а красной краской отметим в каждой стране по одной точке. Всякие две отмеченные точки, лежащие в соседних странах (то есть странах, имеющих общую граничную дугу), соединим внутри этих стран красной дугой так, чтобы красные дуги попарно не пересекались. Тогда всякие две красные точки будут соединены цепочкой дуг, и так как никакие две построенные дуги не будут соединять одни и те же точки, то каждая страна на карте, состоящей из точек и дуг красного цвета, будет ограничена не менее чем тремя дугами. Если какая-то страна на этой карте ограничена более чем тремя дугами, то на её границе можно выбрать две вершины, не соединённые дугой, и соединить их красной дугой внутри этой страны. Повторяя несколько раз эту операцию, мы получим красную карту, на которой каждая страна ограничена ровно тремя дугами. Так как, кроме того, на этой карте никакие две дуги не соединяют одни и те же вершины и так как число вершин больше трёх, то из каждой вершины выходят не менее чем три дуги. Обозначим через n число дуг, через l — число стран, через m — число всех вершин красной карты и через a — число вершин, из которых выходят менее чем шесть дуг. Тогда получим
3l = 2n, |
(1) |
3a + 6(m – a) ≤ 2n. |
(2) |
Из формулы (1) и теоремы Эйлера, применённой к системе точек и дуг красного цвета, следует, что
2n = 6m – 12, |
3a + 6(m – a) ≤ 6m – 12. |
которое показывает, что a≥4. Остаётся заметить, что если некоторая страна на чёрной карте имеет больше пяти соседей, то из отмеченной в этой стране красной точки выходит больше пяти дуг, и потому, в силу неравенства a≥4, на чёрной карте найдутся четыре страны, каждая из которых имеет не больше пяти соседей.
Задача 4. Можно ли семиугольник разрезать на выпуклые шестиугольники?
Решение. Предположим, что какой-то семиугольник удалось разрезать на выпуклые шестиугольники. Обозначим число тех вершин шестиугольников, которые лежат внутри исходного семиугольника, через m, а число оставшихся вершин (то есть лежащих на границе семиугольника) — через m'. В качестве дуг, соединяющих вершины, выберем прямолинейные отрезки сторон многоугольников, удовлетворяющие следующему условию: отрезок должен соединять две вершины и не проходить через остальные вершины. Обозначим через n число таких дуг и через l — число областей, на которые эти дуги делят плоскость (число l на единицу больше числа шестиугольников). Ясно, что любые две вершины окажутся соединёнными цепочкой дуг. В силу теоремы Эйлера
m + m' – n + l = 2. |
(3) |
Так как внешняя область ограничена m' дугами, а каждая из остальных — не менее чем шестью дугами, то
2n ≥ 6(l – 1) + m'. |
(4) |
Из некоторых вершин на границе семиугольника выходят только две дуги. Обозначим число таких вершин через a. Из всякой другой вершины выходят по крайней мере три дуги, так что
3m + 3(m' – a) + 2a ≤ 2n.
Отсюда в силу равенства (3)
n ≤ 3l + a – 6.
Сравнивая это неравенство и неравенство (4), мы получаем
2a – m' ≥ 6. |
(5) |
Так как на границе семиугольника найдутся по крайней мере две вершины, из которых выходят дуги, ведущие внутрь семиугольника, то m' – a ≥ 2. Из этого неравенства и неравенства (5) следует, что a ≥ 8.
С другой стороны, так как семиугольник разрезан на выпуклые многоугольники, то всякая вершина, из которой выходят две дуги, является вершиной семиугольника, и потому a ≤ 7. Таким образом, семиугольник нельзя разрезать на выпуклые шестиугольники.
Как обнаружить фальшивую монету
Шестопал Г.
Представьте себе, что на стол высыпана кучка совершенно одинаковых по виду монет, но вам сказали, что одна из этих монет — фальшивая. Она отличается от остальных монет по весу, но вам не сообщили, легче она или тяжелее. В вашем распоряжении имеются чашечные весы без гирь. Как нужно действовать, чтобы выделить эту монету и выяснить её тип (то есть узнать, легче она или тяжелее) за минимальное число взвешиваний?
Многие из вас, наверное, уже решали эту задачу для 12 монет. На рисунке приведено одно из решений этой задачи. Трём возможным исходам первого взвешивания соответствуют три различных варианта выбора монет для второго взвешивания: на рисунке левая стрелка соответствует случаю, когда перетянула левая чашка, средняя стрелка — равновесию, правая — случаю, когда перетянула правая чашка. Аналогичным образом изображены девять вариантов выбора монет для третьего взвешивания. (На рисунке монеты перенумерованы, буквы Л и Т означают соответственно, лёгкая и тяжёлая.)
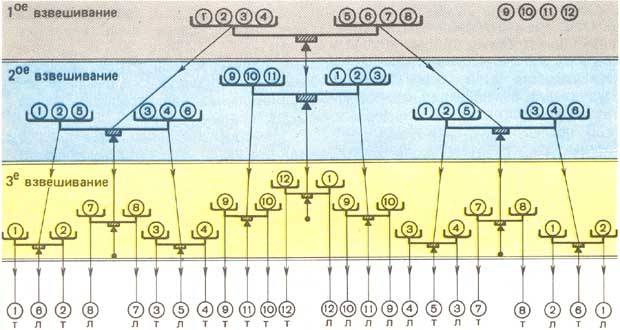
Характерной особенностью этого решения является зависимость выбора монет для очередного взвешивания от результата предыдущего.
Поставим теперь задачу в общем виде.
Имеется m≥3 одинаковых по виду монет. Все монеты, кроме одной, имеют одинаковый вес, а одна отличается от них по весу, но неизвестно, в какую сторону. Каким наименьшим числом взвешиваний на чашечных весах без гирь можно найти эту монету и выяснить её тип? 1
Эта задача более тридцати лет назад привлекла к себе внимание многих математиков, главным образом в Англии и США. В 1945 году в английском журнале «The Mathematical Gazette», похожем по своему направлению на «Квант», появилось решение этой задачи. Его автор Р. Л. Гудстейн впоследствии стал известным специалистом в области математической логики.
Гудстейн указал метод определения фальшивой монеты и её типа за n взвешиваний, n≥3, если число монет
m ≤ ½(3n – 2n + 3)
(заметьте, что для трёх взвешиваний число монет не превышает двенадцати). Однако оказалось, что для n>3 его решение не является лучшим: за n взвешиваний можно выделить фальшивую монету и определить её тип из большего числа монет:
m ≤ ½(3n – 3).
Это обнаружили независимо друг от друга сразу несколько математиков, и в следующем 1946 году тот же журнал опубликовал довольно длинный перечень их имён и разных ступеней успеха, достигнутых на поприще розыска фальшивой монеты. В этом же номере журнала напечатано самое лучшее решение — решение Ф. Дж. Дайсона, будущего известного физика-теоретика.
Идея Дайсона основана на использовании троичной системы счисления: все монеты маркируются специально выбранными троичными числами — маркерами, позволяющими удобно отражать ход последовательных взвешиваний. Особенно привлекательным при этом методе решения оказывается независимость выбора монет для последующего взвешивания от результата предыдущих.
В последующие годы были напечатаны другие решения этой задачи 2, а метод Дайсона был незаслуженно забыт.
Поэтому интересно рассказать о нём подробно.
Всё решение Дайсона можно разбить на два этапа.
А |
Если m = ½(3n – 3), n = 2, 3, ...,
то для выделения одной фальшивой монеты из общего числа m монет и определения её типа достаточно произвести n взвешиваний. |
Б |
Если m < ½(3n – 3), m ≥ 3,
то для достижения той же цели n взвешиваний также будет достаточно. |
Рассмотрим каждый этап в отдельности.
Первый этап
Пусть число монет m = ½(3n – 3).
Рассмотрим все n-значные «троичные числа» (наборы из цифр 0, 1, 2) 00...00, 00...01, ..., 22...22. Их 3n. Используем их для маркировки монет следующим образом: в качестве маркеров возьмём все эти числа, за исключением трёх, состоящих из одинаковых цифр: 0...0, 1...1, 2...2.
«Построим» все маркеры в пары: в одну пару «поставим» два дополнительных маркера — таких, у которых цифры соответствующих разрядов в сумме составляют 2 (другими словами, дополнительными будут те маркеры, сумма которых равна 22...22).
Назовём маркер правым, если в нём первая слева пара неравных цифр — 01, 12 или 20. В противном случае маркер будем называть левым. Очевидно, в каждой паре дополнительных маркеров один всегда будет правым, другой — левым.
Заметим, что число пар маркеров как раз равно общему числу монет m. Перенумеруем монеты номерами от 1 до m и произвольно сопоставим каждой монете одну пару маркеров. Например, 12 монет можно «замаркировать» так, как показано в таблице.
Номер монеты |
Левый маркер |
Правый маркер |
1 |
211 |
011 |
2 |
100 |
122 |
3 |
022 |
200 |
4 |
212 |
010 |
5 |
101 |
121 |
6 |
020 |
202 |
7 |
210 |
012 |
8 |
102 |
120 |
9 |
021 |
201 |
10 |
221 |
001 |
11 |
110 |
112 |
12 |
002 |
220 |
Обозначим соответственно через M(i,0), M(i,1), и M(i,2), множество монет, для которых i-й разряд соответствующего им правого маркера равен 0, 1 или 2.
Легко видеть, что число монет в каждом из множеств M(i,0), M(i,1) и M(i,2) одинаково и что эти множества не имеют общих элементов (см., например, таблицу).
Метод взвешивания монет, придуманный Дайсоном, состоит в следующем:
Производится последовательно n взвешиваний монет.
П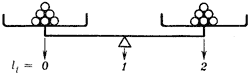 ри
i-м
взвешивании (i
= 1, 2, ..., n)
на левую чашку весов кладутся все монеты
множества M(i,0),
на правую чашку — все монеты множества
M(i,2).
Результат каждого взвешивания будем
обозначать цифрой 0, если перевесила
левая чашка весов, цифрой 1, если обе
чашки имеют одинаковый вес, и цифрой 2,
если перевесила правая чашка (см. рис.).
Результат i-го
взвешивания обозначим через li.
ри
i-м
взвешивании (i
= 1, 2, ..., n)
на левую чашку весов кладутся все монеты
множества M(i,0),
на правую чашку — все монеты множества
M(i,2).
Результат каждого взвешивания будем
обозначать цифрой 0, если перевесила
левая чашка весов, цифрой 1, если обе
чашки имеют одинаковый вес, и цифрой 2,
если перевесила правая чашка (см. рис.).
Результат i-го
взвешивания обозначим через li.
Из цифр l1, l2, ..., ln составим маркер 3
l = l1 l2 ... ln.
Оказывается, l — маркер фальшивой монеты F и если l — правый маркер, то F тяжелее остальных монет, а если l — левый маркер, то F легче остальных монет.
Действительно, посмотрим, что происходит, когда производится i-e взвешивание. В результате этого взвешивания весы либо остались в равновесии, либо одна из чашек перевесила.
Если весы остались в равновесии, то фальшивой монеты на них нет, следовательно, она — в множестве M(i,1). Но это означает, что i-й разряд её правого (и левого) маркера равен 1, на что и указывает результат взвешивания li = 1.
Если одна из чашек весов перевесила, то фальшивая монета лежит на весах. Пусть, например, перевесила правая чашка, т.е. li = 2. Этот результат возможен в двух случаях:
— фальшивая монета лежит на правой чашке (тогда она тяжелее остальных монет), значит, она находится во множестве M(i,2), i-й разряд её правого маркера равен 2, следовательно, результат взвешивания совпадает с i-м разрядом её правого маркера;
— фальшивая монета лежит на левой чашке (тогда она легче остальных монет), значит, она находится во множестве M(i,0), следовательно, i-й разряд её правого маркера равен 0 и результат взвешивания совпадает с i-м разрядом её левого маркера.
Совершенно аналогичен «симметричный» случай, когда перевесит левая чашка весов (li = 0).
Поэтому, действительно, сформированный в результате последовательных взвешиваний маркер l = l1 l2 ... ln есть маркер фальшивой монеты, притом правый в случае более тяжёлой монеты и левый — в случае более лёгкой, что и требовалось доказать.
Интересно отметить, что тип монеты, как правило, определится раньше, чем произведены все взвешивания, — как только в процессе формирования маркера l появятся две различные цифры.
Существенной особенностью описанного метода, как уже было отмечено раньше, является то обстоятельство, что выбор монет для каждого взвешивания не зависит от результатов предыдущих взвешиваний.
Например, для 12 монет, замаркированных так, как показано в таблице, нужно проделать такие три взвешивания: (1,4,7,10) – (3,6,9,12), (3,6,9,10) – (2,5,8,12), (3,4,8,12) – (2,6,7,11).
Второй этап
Коротко наметим метод Дайсона для случая m < ½(3n – 3).
Если в этом случае монетам сопоставлять маркеры произвольно, то в множествах M(i,0) и M(i,2) может оказаться разное число монет. Поступим поэтому следующим образом. Разобьём все маркеры на группы по шесть: в одну группу отнесём правые маркеры, получающиеся друг из друга циклической заменой цифр 0 → 1, 1 → 2, 2 → 0 и соответствующие им левые маркеры.
В каждой группе окажется по три правых маркера и три левых маркера. Группу, содержащую правые маркеры 00...01, 11...12, 22...20, выделим особо. Разобьём монеты на группы по три, пока это возможно, и замаркируем их следующим образом. Монетам из одной группы сопоставим пары маркеров из одной группы, а для остатка, если он есть, используем пары маркеров из выделенной группы. Если останется одна монета, не вошедшая в тройки, то сопоставим ей правый маркер 11...12, а если две, — то правые маркеры 00...01 и 22...20 (и соответствующие левые маркеры).
При такой маркировке первые n–1 взвешиваний производятся по старым правилам. Как производить последнее взвешивание, сообразите самостоятельно.
М етод
Дайсона описан. Убедимся теперь, что он
в определённом смысле является наилучшим.
А именно, покажем, что если из m
монет можно выделить n
взвешиваниями фальшивую монету и
определить её тип, то 2m
≤ 3n
– 3. Разумеется, мы не будем учитывать
возможного «везения»: при нём для
определения фальшивой монеты из любого
числа монет может хватить и двух
взвешиваний.
етод
Дайсона описан. Убедимся теперь, что он
в определённом смысле является наилучшим.
А именно, покажем, что если из m
монет можно выделить n
взвешиваниями фальшивую монету и
определить её тип, то 2m
≤ 3n
– 3. Разумеется, мы не будем учитывать
возможного «везения»: при нём для
определения фальшивой монеты из любого
числа монет может хватить и двух
взвешиваний.
Итак, предположим, что n взвешиваний достаточно.
Занумеруем монеты числами 1, 2, ..., m и приготовим 2m бумажек. Напишем на них все возможные варианты: первая монета легче, первая монета тяжелее, вторая монета легче и т.д. Ясно, что при этом все 2m бумажек окажутся использованными и ни один из возможных вариантов не будет упущен. Будем обозначать, как мы условились выше, результат взвешивания цифрами 0, 1 или 2. Каждое взвешивание показывает, что часть возможных ответов не подходит, а часть — остаётся под подозрением. Отберём монеты для первого взвешивания. Не производя его фактически, напишем на каждой из бумажек тот результат первого взвешивания, который оставляет её под подозрением. Ясно, что на каждой бумажке будет написана одна из цифр 0, 1 или 2. Таким образом, все бумажки будут разбиты на три группы. Поэтому в наиболее многочисленной группе окажется не меньше 2m/3 бумажек. Значит, как бы мы ни организовывали первое взвешивание, может оказаться, что после него под подозрением останутся не меньше 2m/3 бумажек.
Аналогично, второе взвешивание рассортирует эту подозрительную группу на три подгруппы. Поэтому в наиболее многочисленной из них окажется не меньше 2m/9 бумажек. Точно так же после n взвешиваний мы можем получить 2m/3n подозрительных бумажек в одной группе. Следовательно, если 2m/3n > 1, то фальшивая монета и её тип, вообще говоря, за n взвешиваний определены быть не могут. Поэтому если n взвешиваний достаточно, то 2m ≤ 3n.
Но это ещё не всё! Мы не разобрались ещё со случаем 2m = 3n – 1 (чётное число 2m не может равняться ни 3n – 2, ни 3n). Для него изложенных выше соображений недостаточно.
Рассмотрим более внимательно первое взвешивание. Ясно, что число бумажек, на которых написана цифра 0, равно числу бумажек, на которых написана цифра 2. Пусть тех и других — по p штук, тогда на 2m – 2p бумажках будет написана 1.
Заметим, что p — чётное число. Действительно, если на левой и правой чашке весов лежит по k монет, то p = 2k. Если p или 2m – 2p больше 3n–1, то по рассмотренному для определения нужной бумажки может не хватить оставшихся n–1 взвешиваний. Если же p = 2k ≤ 3n–1 и 2m – 2p ≤ 3n–1 – 1, то, поскольку 3n–1 — число нечётное, p ≤ 3n–1 – 1, 2m – 2p ≤ 3n–1 – 1. Но тогда 2m = (2m – 2p) + 2p ≤ 3n–1 – 1 + 2(3n–1 – 1) = 3n – 3. Итак, если n взвешиваний достаточно, то 2m ≤ 3n – 3.
В заключение — несколько задач, которые могут быть решены методом Дайсона.
Как начиналась геометрия
Смилга В. П.
Истинное начало этой истории теряется во мгле времён.
Где, как и когда начиналась геометрия?.. Где, как и когда обрела она законченную форму и заслужила право называться наукой?.. Кто был тот неведомый, первый, предложивший аксиоматическое её построение? Не знаем и, вероятно, не узнаем.
Принято думать, что это сделали греки. Быть может, прославленные египетские жрецы или не менее прославленные халдейские маги суть истинные отцы этой науки. Но они не озаботились тем, чтобы оставить для потомков труды, подтверждающие их приоритет.
Как бы то ни было, в седьмом веке до нашей эры геометрия приходит в Грецию. И здесь греки, поклонники холодной логики и филигранного изящества чистого интеллекта, любовно оттачивают (или, быть может, создают?) одно из самых красивых и долговечных творений человеческой мысли — науку геометрию.
Тогда-то и начинается азартная и драматическая игра в чистую логику, затянувшаяся вот уже на два с половиной тысячелетия...
Фалес
Предполагают, что геометрию начинала Ионийская школа, а точнее, сам её основатель — Фалес Милетский, проживший что-то около сотни лет (640–540 или 546 годы до нашей эры).
Толком мы мало что знаем о нём.
Точно известно, что имел он титул одного из семи мудрецов Греции, что по официальному счёту идёт как первый философ, первый математик, первый астроном и вообще первый по всем наукам в Греции. По-видимому, он был тем же для Греции, что Ломоносов для России. В молодости Фалес попал в Египет, куда фараон Псамметих только-только начал допускать иностранцев. Вероятно, он оказался там по торговым делам — известно, что свою карьеру Фалес начинал купцом.
В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Потом он вернулся домой и основал философскую школу, выступая, очевидно, не столько как самостоятельный мыслитель, сколько как популяризатор египетской мудрости.
Считается, что геометрию и астрономию привёз именно он.
Что именно сделал он в геометрии, мы можем только гадать, хотя греческие авторы приписывали ему довольно много.
Например, Прокл Диддох утверждает, что Фалес доказал теоремы о равенстве вертикальных углов, о равенстве углов при основании равнобедренного треугольника, о том, что диаметр делит круг пополам и ещё ряд других.
Допустив даже, что все историки писали сущую истину, мы не можем сказать, самостоятельно ли Фалес пришёл к этим теоремам или просто пересказал идеи египтян.
По-видимому, единственный бесспорный факт из его научной деятельности — предсказание солнечного затмения 585 года до нашей эры. Но легенд о Фалесе ходило множество, и это само по себе доказывает, что учёный он был крупный.
Во всяком случае, одному у него могут поучиться все философы: краткости. Полное собрание его сочинений (разумеется, до нас не дошедшее) по преданию составляло всего 200 стихов.
Пифагор
Ученики и последователи Фалеса уделяли немало внимания геометрии в своих учёных занятиях. Однако центральной математической школой в VI–V веках до нашей эры была, несомненно, Пифагорейская.
Б иографические
сведения о Пифагоре в основном сводятся
к нескольким анекдотам. В этом он очень
походит на Фалеса Милетского. Неясности
начинаются уже с вопроса о его
происхождении. Бертран Рассел, суммируя
имеющиеся данные, заключает: «Некоторые
говорят, что он был сыном состоятельного
гражданина по имени Мнесар, другие же
считают, что он был сыном бога Аполлона.
Я предоставляю читателю выбирать между
двумя этими противоположными версиями».
иографические
сведения о Пифагоре в основном сводятся
к нескольким анекдотам. В этом он очень
походит на Фалеса Милетского. Неясности
начинаются уже с вопроса о его
происхождении. Бертран Рассел, суммируя
имеющиеся данные, заключает: «Некоторые
говорят, что он был сыном состоятельного
гражданина по имени Мнесар, другие же
считают, что он был сыном бога Аполлона.
Я предоставляю читателю выбирать между
двумя этими противоположными версиями».
Полагают, что жил Пифагор столь же основательно, что и Фалес, — около ста лет (предположительно 560–470 или 580–500 годы до нашей эры, что для нас почти одно и то же). Опять же, как и Фалес, он лет двадцать набирался мудрости в Египте; затем (и в этом он Фалеса превзошёл) ещё лет десять жил в Вавилоне, где тоже поднакопил знаний. Утверждают также, что он путешествовал по Индии, но этому никто не верит.
В каждой второй брошюре о боксе можно прочитать, что Пифагор был олимпийским чемпионом по кулачному бою, хотя первоисточник столь любопытных данных никогда не указывается (по крайней мере мне он не известен). Приятно, впрочем, сознавать, что философ и математик может оказаться боксёром экстра-класса.
Но если насчёт боксёрских данных Пифагора и есть некоторые сомнения, то о его активном, хотя и не очень удачном, вмешательстве в политику мы знаем наверняка. Известно, например, что граждане сицилийского города Кротона, где он основал по возвращении из дальних стран свою школу и попутно втравил весь город в тяжёлую междоусобную войну, в итоге попросили его убраться вместе со школой. Это он и сделал, и довольно поспешно, что было разумно и своевременно.
Особых восторгов как личность Пифагор не вызывает, хотя, несомненно, учёным он был очень сильным. Его Пифагорейский орден философов и математиков слишком уж напоминает казарму, а сам основатель и глава подозрительно смахивает на какого-то фюрера, хотя и несравненно более культурного, чем те, что имели успех в двадцатом столетии.
Это нам Пифагор представляется в основном математиком. Сам же он, как и его современники, полагал, что истинная его профессия — пророк. А как известно, каждый пророк обязан отчасти быть фокусником, отчасти демагогом, отчасти шарлатаном. Всем этим Пифагор, видимо, владел в полном ассортименте. А ученики, стараясь по мере сил, распространяли в массах доказательства богоизбранности учителя. Рассказывали, что у него было золотое бедро; рассказывали, что достойные люди видели его одновременно в двух разных местах; рассказывали также, что когда однажды он переходил вброд реку, последняя от восторга вышла из берегов, радостно восклицая: «Да здравствует Пифагор!». (На мой взгляд, речной бог выбрал не лучший способ прославления, ибо в первую очередь Пифагор должен был изрядно вымокнуть. Но так передавали эту историю ученики.)
Говорят также, что он читал проповеди скотам, поскольку мало различал их и людей.
Именно сам Пифагор — очевидно, для пущего авторитета — распространял, популяризировал, холил и лелеял идею, что его родитель не кто иной, как светоносный и лучезарный Аполлон (задав тем самым немало лишней работы своим биографам).
Кроме того, Пифагор оказался истинным отцом популярного и ныне обычая — присваивать научные результаты своих учеников. Причём дело было поставлено вполне официально: существовал декрет, по которому авторство всех математических работ школы приписывалось Пифагору. Хотя подобные вещи не такая уж редкость и в наши дни, всё же двадцать пять столетий несколько смягчили и облагородили нравы. Великий же Пифагор вообще вне конкуренции на этой стезе. Он исхитрился устроить так, что верные ученики объявляли его автором работ, выполненых намного позже его кончины.
Понятно, что при таких порядках наиболее безусловным и безоговорочным научным доводом в Пифагорейской школе считалась ссылка на «самого». Так и говорили на хорошем древнегреческом языке: «Сам сказал». После чего дискуссия была неуместна и даже несколько опасна.
Далее, решения математических задач тщательно засекречивались. Были и другие «табу», сведённые в подробный список, слегка напоминающий творчество сумасшедшего руководителя детского сада. Опасаясь показаться голословным, я процитирую часть правил хорошего тона для джентльменов из Пифагорейского клуба. Вот они:
Воздерживайся от употребления в пищу бобов.
Не поднимай то, что упало.
Не прикасайся к белому петуху.
Не откусывай от целой булки.
Не ходи по большой дороге.
Вынимая горшок из, огня, не оставляй следа его на золе, но помешай золу.
И так далее, все в том же духе.
И эта компания время от времени захватывала власть то в одном, то в другом греческом городе, устанавливая там культ Пифагора и, соответственно, требуя выполнения своего устава. Правда, как меланхолически замечает Бертран Рассел, «те, которые не были возрождены новой верой, жаждали бобов и рано или поздно восставали».
Как уже было сказано, накопленные знания пифагорейцы тщательно скрывали. И, кто знает, может быть, геометрия осталась бы неизвестной всему человечеству до самых наших дней, если бы не оплошность одного из рядовых членов Пифагорейской школы. Вот как пифагорейцы объясняли, почему геометрия стала открыто распространяться. Это произошло по вине одного из них, который потерял деньги общины. После этого несчастья община позволила ему зарабатывать деньги, преподавая геометрию, — и геометрия получила название «Предание Пифагора».
Любопытно, что, судя по всему, существовал учебник геометрии с таким названием.
Что же касается истории с деньгами, если в ней есть зерно истины, я, хотя не считаю себя злорадным человеком, был бы счастлив узнать, что наш пифагореец отнюдь не потерял деньги, а прокутил их в ближайшем портовом кабачке, потягивая вино, наслаждаясь похлёбкой из белого петуха с бобовой приправой, с удовольствием кусая от целой булки и распевая затем негармоничные песни на большой дороге. [Всё-таки встряну со своим комментарием. Сегодня, через две с половиной тысячи лет Пифагор со своими «правилами хорошего тона» может показаться странным и даже неумным. Но, во-первых, ещё Литлвуд призывал не относиться к античным классикам снисходительно: «Греки — это не способные школьники или хорошие студенты, но, скорее, "коллеги из другого колледжа"». А во-вторых, в книге Пифагора «Золотой канон. Фигуры эзотерики» (М., Эксмо, 2004), где комментарии гораздо более уважительны, пятое правило приводится в следующем виде:
Не следует ходить торными дорогами. Избегая торных дорог (по которым идёт большинство), ходи тропинками.
Так что этот совет больше на эппловское «Think different» смахивает, чем на бред сумасшедшего. — E.G.A.]
На этом мы и расстанемся с Пифагором. Нам предстоит отметить великие заслуги перед геометрией ещё одного малоприятного, на мой вкус, человека.
Платон
Платон, живший в 428–348 годах до нашей эры, считается, и, должно быть, справедливо — я не специалист — одним из величайших философов Греции.
Геометрия ко времени Платона уже была очень развита. Было решено много весьма и весьма сложных задач, доказаны сложнейшие теоремы. Но ясной позиции во взглядах на общую схему построения науки ещё не было. Развитие геометрии, как нередко бывает в науке, стимулировалось задачами, решения которых никак не удавалось отыскать. Требовалось при помощи циркуля и линейки, не привлекая никаких других геометрических инструментов:
разделить данный угол на три равных части (трисекция угла);
построить квадрат с площадью, равной площади данного круга (квадратура круга);
построить куб с объёмом, в два раза большим объёма данного куба (делосская задача).
Только в конце прошлого века было доказано, что в такой постановке ни одна из этих задач не может быть решена, хотя, если использовать другие геометрические инструменты или (что то же) использовать при построении геометрические места точек, отличные от прямой либо дуги окружности, то все три задачи легко решаются.
Однако принятые у греков правила игры не позволяли пользоваться при решении задач ничем, кроме циркуля и линейки. Платон даже обосновал это ссылкой на авторитет богов.
Так что ни одна из проблем решена не была, но по ходу дела геометрия была основательно разработана.
Я с великим сожалением опускаю все анекдоты, связанные с этими задачами. Историй много, и все они прелестны, но нельзя слишком отвлекаться. Вспомню лишь одно из преданий, связанное именно с Платоном и показывающее его с лучшей стороны.
Однажды, рассказывает Эратосфен, на острове Делосе вспыхнула эпидемия чумы. Жители острова, естественно, обратились к Дельфийскому оракулу, который повелел удвоить объём золотого кубического жертвенника Аполлону, не изменяя его формы. За советом обратились к Платону. Платон задачи не решил, но зато истолковал оракула в том смысле, что боги гневаются на греков за нескончаемые междоусобные войны и желают, чтобы они, греки, вместо кровавых побоищ занимались бы науками и особенно геометрией. Тогда чума исчезнет.
Платон очень много сделал для развития математики и весьма ценил её. На входе в его академию был даже высечен весьма категорический лозунг: «Да не войдёт сюда тот, кто не знает геометрии». Дело в том, что Платон полагал: «Изучение геометрии приближает к бессмертным богам» — и воспитывал в этом духе своих учеников, приплетая математику к месту и не к месту.
По-видимому, Платон первый чётко потребовал: математика вообще и геометрия в частности должны быть построены дедуктивным образом. Иначе говоря, все утверждения (теоремы) должны строго логически выводиться из небольшого числа основных положений — аксиом. Такая постановка — крупнейший шаг вперёд.
Некоторые из учеников Платона выросли в блестящих геометров. Но надо сказать, что и по своим взглядам, и по методам организации школы, и по любви к саморекламе Платон очень напоминает Пифагора.
На мой взгляд, как философ и как человек, Платон довольно несимпатичен. Во всяком случае, созданная им теория идеального государства, образцом которого послужила реальная и вполне фашистская страна — Спарта — восторга, мягко говоря, не вызывает. Основные положения его утопии в общем удовлетворяют требованиям нацистов. Всю свою жизнь он яростно боролся против демократии в политической жизни и против материализма в духовной. Философов-материалистов Платон не только абстрактно поносил в своих философских сочинениях, но, демонстрируя неплохую практическую хватку, нередко дискутировал, как сказали бы теперь, «в жанре политического доноса».
Приведу пример. Был в те времена в Греции замечательный философ, один из первых материалистов — Анаксагор. (Мы почти ничего не знаем о его геометрических работах; известно, однако, что в темнице, где ему пришлось сидеть за свои взгляды, он исследовал проблему квадратуры круга.)
И вот Платон в одном из сочинений — в диалоге жителя Афин (рупор самого Платона) и спартанца — так расправляется с Анаксагором.
Афинянин: «Когда мы, стремясь получить доказательства существования богов, ссылаемся на Солнце, Луну, Звёзды и Землю как на божественные существа, то ученики этих новых мудрецов возражают нам, что всё это ведь только земля и камни, и они (т.е. камни) совершенно не в состоянии заботиться о людских делах».
Спартанец молниеносно чует ересь и возмущённо восклицает: «Какой же вред для семьи и государства проистекает от таких настроений у молодёжи!».
Так дискутировал Платон.
Евклид
К IV–III векам до нашей эры геометрия вполне оформилась как наука. Были устоявшиеся традиции, детально разработанные методы решения задач, крупные достижения, было уже несколько учебников и различные научные школы.

Рассказать обо всех геометрах доевклидового периода — а список математиков того времени включает несколько десятков славных имён — и об их работах, естественно, невозможно. И поскольку у нас не многотомный исторический труд, а небольшая статья, оставим предтеч и перейдём непосредственно к Евклиду.
Жил и работал он во время весьма любопытное.
В 323 году до нашей эры то ли вследствие острой лихорадки, то ли в результате неумеренного пьянства или просто от доброй порции яда отправился на свидание к отцу своему Зевсу царь царей земных, изрядно уже потрёпанный жизнью, хотя сравнительно молодой, тридцатитрёхлетний мужчина — Александр Македонский.
Полубога подобающим образом проводили и перешли к текущим делам. А дел хватало: надо было делить империю. Размеры её были невероятны. Всего лишь за десять лет оказались завоёванными страны, в сотни раз превосходившие маленькую полунищую Македонию.
Границы известного мира расширились во много раз, и теперь предстояло переварить проглоченное. Было ясно, что для одного такое наследство непомерно, и отдавать всё малолетнему брату Александра или же второму наследнику — сыну, появившемуся на свет через несколько месяцев после смерти отца, было просто смешно. Посему империю полюбовно растащили те полководцы, которых Александр не успел казнить. Они поклялись в вечной дружбе, заключили вечный мир, порядком выпили на радостях, обменялись суровыми мужскими пожатиями на прощанье — и, естественно, началась междоусобная резня.
Более других в этой сваре повезло осмотрительному Птолемею, который при делёжке отхватил себе Египет. Наследники его постепенно ассимилировались, а династия оказалась не только самой прочной и долговечной, но и прославилась тем, что дала истории Клеопатру.
И самый первый Птолемей, и все последующие Птолемеи славны тем, что были покровителями наук. Какие у них на то были мотивы, трудно сейчас разобраться, но факты таковы: в III–II веках до нашей эры Александрия превратилась в основной научный центр эллинистического мира. И наиглавнейшим научным институтом был знаменитый Александрийский музей с Александрийской библиотекой. Сюда-то и пригласил Птолемей Евклида, и именно здесь Евклид написал «Начала» — книгу, в истории человечества бесспорно уникальную.
Снова я должен сделать традиционное уже признание: о самом Евклиде практически ничего не известно.
Легенды, конечно же, имеются. Рассказывают, например, что Птолемей поначалу сам захотел одолеть премудрости геометрии, но довольно скоро обнаружил, что изучение математики требует некоторых усилий. Тогда он призвал Евклида и вопросил его, полагаю, как джентльмен джентльмена, нельзя ли постигнуть все тайны науки как-нибудь попроще? На что Евклид ответил: «В геометрии нет царского пути». Остаётся неведомым, продолжал ли после этого царь занятия математикой (вероятнее всего, он утешился в занятиях, более приличествующих царям, — таких, как приёмы, охота, пиры, услады гарема, наконец).
Рассказывают также, что однажды к Евклиду явился изучать геометрию некий молодой прагматик. Первый вопрос, который он задал будущему учителю, был следующий: какая практическая польза будет от штудирования «Начал»? Тогда Евклид, весьма и весьма задетый, призвал раба и сказал: «Дай ему обол (грош), он ищет выгоды, а не знаний».
Надо, впрочем, сознаться, что обе истории столь традиционны, учитывая представление древних греков о мудрецах и о математике, что особо доверять им не приходится. «Точные» же биографические данные основываются на заметках неизвестного арабского математика XII века: «Евклид, сын Наукрата, сына Зенарха, известный под именем Геометра, учёный старого времени, по своему происхождению грек, по местожительству сириец, родом из Тира...»
Всё.
Человек бесследно растворился в веках. Осталась его работа.

 Рис.
1.
Рис.
1.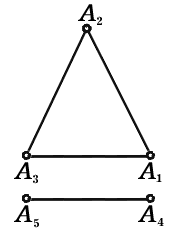 Рис.
2.
Рис.
2.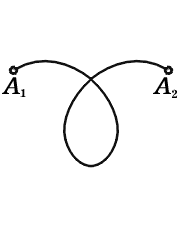 Рис.
3.
Рис.
3.