1.2.2. Методи згладжування зображень;

Для заданого M×N зображення f(x,y) операції побудови згладженого зображення g(x,y) полягає у визначені середнього значення пікселів в околі кожної точки (x,y).Згладжене зображення отримується за співвідношенням

g(x,y) =

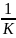
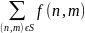
для х=0,1,….,М -1, у=0,1,….,N-1. S - множина координат точок в околі точки (х,у),включаючи її саму. К – загальна кількість точок в околі. Якщо використовувати окіл 3х3, то порівнюючи рівняння бачимо,що є частковий випадок останнього з wі=1/9. Зауважимо,що ступінь згладжування пропорцій до розміру вибраного околу.

Ефект згладжування може бути зменшений використанням порогового критерію. Замість використання ми утворюємо g(x,y) за таким правилом:

g(x,y) = , якщо

у протилежному випадку

де Т – порогове значення. Такий підхід залишає без зміни області зображення з великим, порівняно з Т відхиленням рівнів сірого тону. Можна очікувати, що більші відхилення відповідають контурам, тому використання умови приведе до зменшення нечіткості контурів.

1.2.3. Методи підсилення різкості;

Для визначення країв на зображенні використовують градієнтний метод. Край - це границя між двома областями з порівняно різними властивостями сірого тону. Для заданої функції f(x,y) градієнт f від координат (х,у) визначається як вектор

[f(x,y)] = =[ ] (1)

.Для визначення країв між областями на зображенні нас цікавить модуль вектора, який позначається G[f(x,y)], при чому

[f(x,y)] = [G ²+Gy²]^1/2 (2)

Ця величина дорівнюя максимальній швидкості зростання f(x,y) у напрямку G.

На практиці градієнт наближають сумою абсолютних значень похідних:

G[f(x,y)] = (3)

Таке наближення значно легше реалізувати. Похідні градієнта за х та за у обчислюють за формулами

т × Gy = т × (4)

Маски та називаються операторами Собеля.

-1	-2	-1			-1	0	1
0	0	0			-2	0	2
1	2	1			-1	0	1

а б

Рис.4. Оператори Собеля:

а – для обчислення 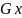; б – для обчислення Gy

Щоб отримати градієнт використовують комбінацію (2) або (3). Згортка цих масок із зображенням f(x,y) дає градієнт в усіх точках зображення і його називають градієнтним зображенням. Існують багато способів побудови градієнта зображення з використанням порогових значень. Нижче наведено можливі варіанти побудови градієнтних зображень:

а) підсилення важливих країв із збереженням особливостей гладкого фону:

g(x,y) =

б) задавання країв певним рівнем сірого кольору, фон залишається без зміни:

g(x,y) =

де L_{G –} рівень сірого тону для країв;

в) вивчення зміни сіпого тону країв без впливу фону:

g(x,y) =

де L_{B –} рівень сірого тону для фону;

г) побудова бінарного градієнтного зображення,де краї і фон зображенні двома різними сірими тонами:

g(x,y) =

де L_G - рівень сірого тону для країв, а L_{B –} рівень сірого тону для фону,Т – порогове значення, яке підбирають експериментально.

Також підсилюють різкість зображення за допомогою оператора Лапласа.

Оператор Лапласа визначається за формурлою

=

який наближено можна очислити згортанням маски (рис.5) із зображенням 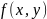.Якщо вектор сформований із коефіцієнтів цієї маски,ми можемо виразит оператор Лапласа у формі:

=

0	1	0
1	-4	1
0	1	0

Рис.5.Маска для обчислення оператора Лапласа

Покращення зображення за допомогою оператора Лапласа виконується за формулою

g(x,y) = -

де – вхідне зображення, g(x,y) – покращене зображення, - лапсасіан.

Зауважимо, що оператор Лапласа є диференціальним,він підсилює різкість зображення,але перетворює області з постійними значеннями яскравості в 0. Додавання оригінального зображення відновлює тональність таких областей. Цей оператор також застосовують як детектор для встановлення належності даного піксела темній або стороні краю.