6. Применение критерия Хи-квадрат Пирсона для выявления связи между номинативными переменными

Связь между номинативными переменными можно интерпретировать и как зависимость, и как различие между выборками, т.к. градации номинативной переменной можно рассматривать как признаки принадлежности к разным группам.

Например, номинативная переменная «пол», имеющая две градации (мужской и женский) и переменная «темперамент», имеющая 4 градации (холерик, сангвиник, меланхолик, флегматик).

Первый вариант формулировки вопроса: существует ли связь между полом и темпераментом? (Зависит ли темперамент от пола? Связаны ли пол и темперамент?)

Второй вариант формулировки вопроса: различаются ли мужчины и женщины по темпераменту (по представленности различных типов темперамента?). В этом случае градации переменной «пол» выступают в качестве признака принадлежности к одной из сравниваемых групп.

Рассмотрим наиболее часто встречающиеся случаи анализа связи между двумя номинативными переменными.

А) Обе переменные имеют по 2 градации.

Форма представления – четырехпольная таблица.

Введем необходимые обозначения в четырехпольной таблице:

		2-я переменная
		Градация 1	Градация 2	ВСЕГО
1-я переменная	Градация 1	А	В	A+B
	Градация 2	С	D	C+D
	ВСЕГО	A+C	B+D	n=A+B+C+D

Формула для вычисления значения критерия Хи-квадрат в случае четырехпольной таблицы следующая:

Число степеней свободы k для четырехпольной таблицы всегда равно 1 (число номинаций M (классов) минус 1). Поэтому критические значения , , (см. Приложение 4).

Вычисленное значение хи-квадрат сравнивается с критическими, начиная с меньшего, и по тому, какого из них оно больше, делается вывод о наличии статистически значимой связи на соответствующем уровне значимости.

Если же вычисленное значение не превышает меньшего из критических, то делается вывод о том, что достоверной связи между переменными не выявлено.

Графическое представление четырехпольной таблицы возможно в следующих вариантах:

А) две круговые диаграммы по каждой из двух выборок, расположенные рядом для удобства сопоставления, построение – по процентам (в Excel проценты при построении круговых диаграмм вычисляются автоматически);

Б) гистограмма, также построенная по процентам (для этого четырехпольная таблица пересчитывается в Excel в процентом выражении):

		2-я переменная
		Градация 1	Градация 2	ВСЕГО
1-я переменная	Градация 1	=100*А/(А+В)	=100*В/(А+В)	A+B
	Градация 2	=100*С/(С+D)	=100*D/(С+D)	C+D
	ВСЕГО

Б) Одна переменная имеет 2 градации, вторая – больше.

Форма представления – многопольная таблица.

		2-я переменная				ВСЕГО
		Градация 1	Градация 2	…	Градация М
1-я переменная	Градация 1	A11	A12		A1M	A1i
	Градация 2	A21	A22		A2M	A2i
	ВСЕГО	A11+A21	A12+A22		A1M+A2M	A1i+A2i

В этом случае формула для вычисления .

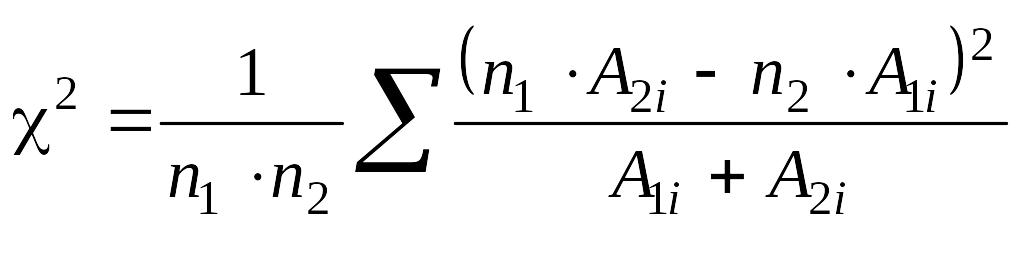Число степеней свободы в случае многопольной вычисляется как , где M – число градаций признака.

Графическое представление многопольной таблицы – как и четырехпольной.

В качестве примера рассмотрим часто встречающийся случай обработки результатов анкетирования респондентов, когда они могут, отвечая на вопросы анкеты, выбирать несколько вариантов ответа.

На каждый вариант каждого ответа отводится отдельный столбец, если вариант выбран – ставится 1, если нет – 0. Совокупность вариантов ответа на один вопрос представляет собой «блок» в сводной таблице исходных данных.

В исследовании выявлялись особенности внтуриличностных и внутригрупповых конфликтов у студентов разных ВУЗов с учетом пола и года обучения. Размещаем данные на новом листе и называем его «Бинарные».

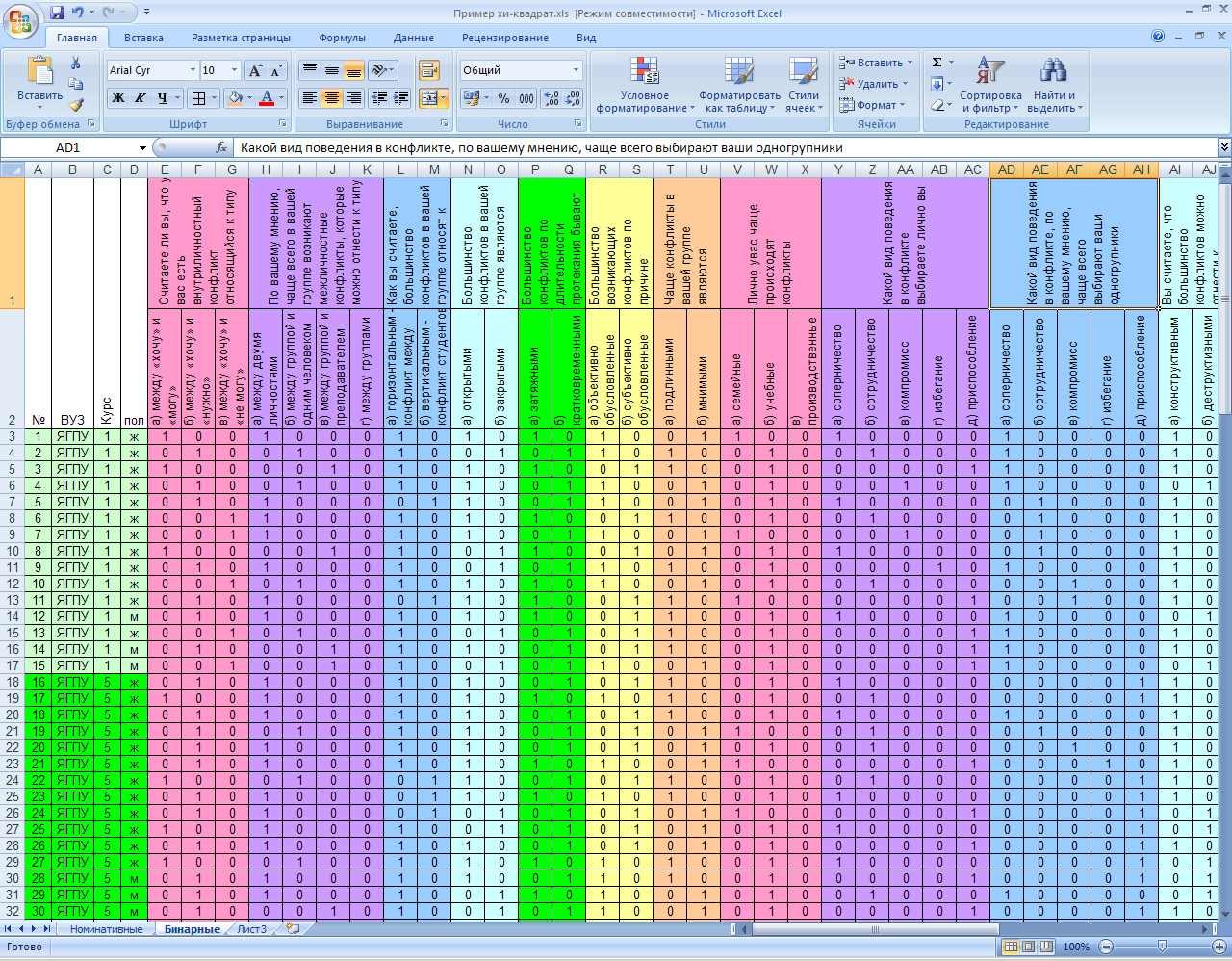
Предположим, нас интересует вопрос, различаются ли 1-й и 5-й курсы по представленности внутриличностного конфликта между «хочу» и «могу» (другими словами – существует ли связь между тем, на каком курсе обучается студент, и тем, насколько представлен у него конфликт между «хочу» и «могу»).

Тогда 1-я переменная – это номер курса, а 2-я – наличие данного конфликта.

		Конфликт между «хочу» и «могу»
		ДА	НЕТ	ВСЕГО
Курс	1-й	3	12	15
	5-й	4	11	15
	ВСЕГО	7	23	30

Подставляем значения ячеек таблицы в формулу

Так как вычисленное значение хи-квадрат меньше самого первого критического , то делается вывод: «Статистически достоверного различия между первокурсниками и пятикурсниками по представленности (частоте встречаемости) внутриличностного конфликта между «хочу» и «могу» не выявлено».

Однако, если столбцов в таблице много, построение четырехпольных таблиц для каждого столбца займет много времени. Автоматизируем процесс.

На новом листе «Хи-кв» подготовим вспомогательную таблицу по количеству 1 (ДА) и 0 (НЕТ) в каждом столбце по курсам раздельно:

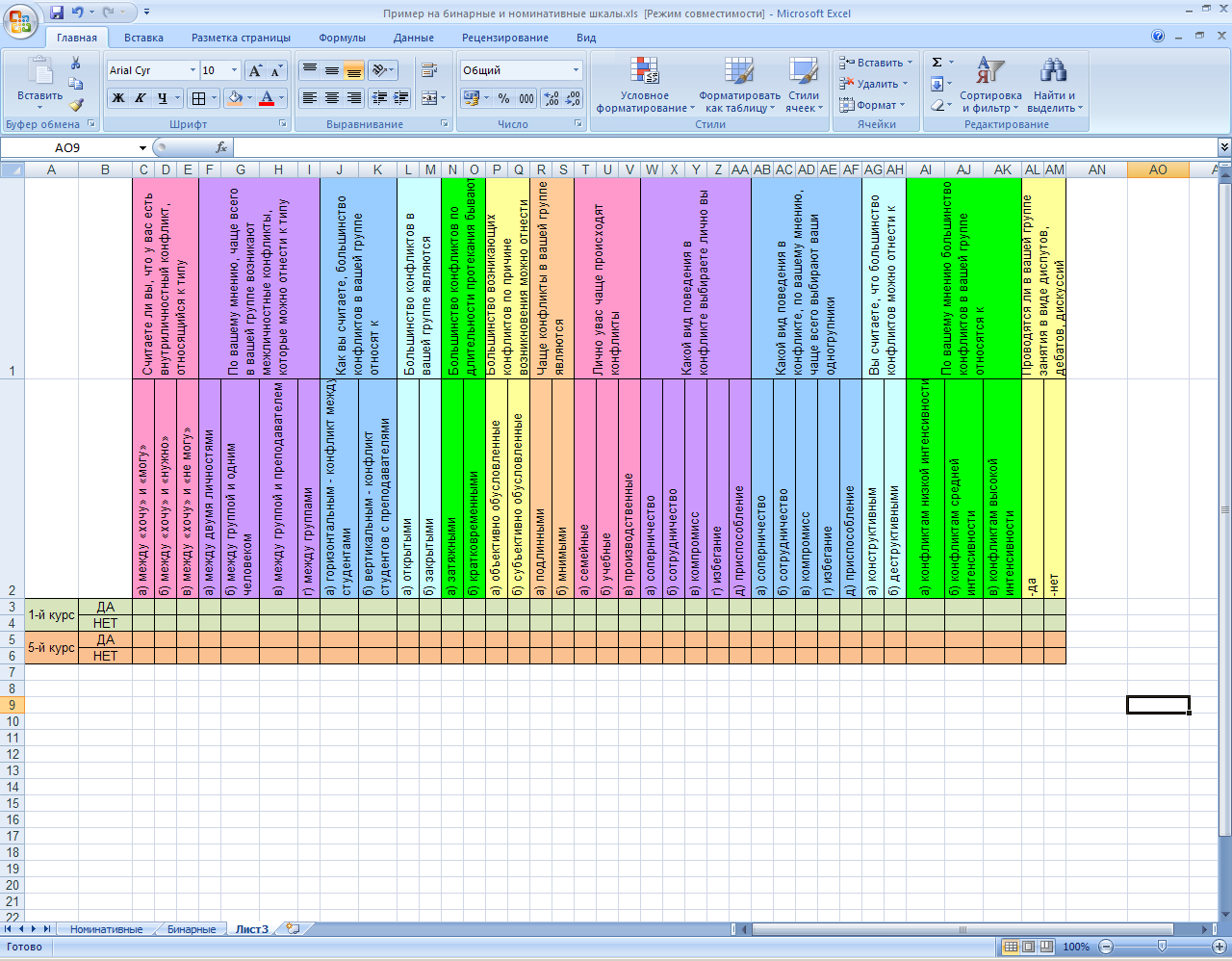
Вычислим количества нулей и единиц, воспользовавшись функцией СЧЕТЕСЛИ(), которая считает количество значений в выделенном диапазоне, соответствующих определенному условию.

Сначала вычислим количество единиц в столбце «а) между хочу и могу» только для первого курса ЯГПУ.

Установим курсор в ячейку «Да, есть конфликт между хочу и могу» и вызовем функцию СЧЕТЕСЛИ:

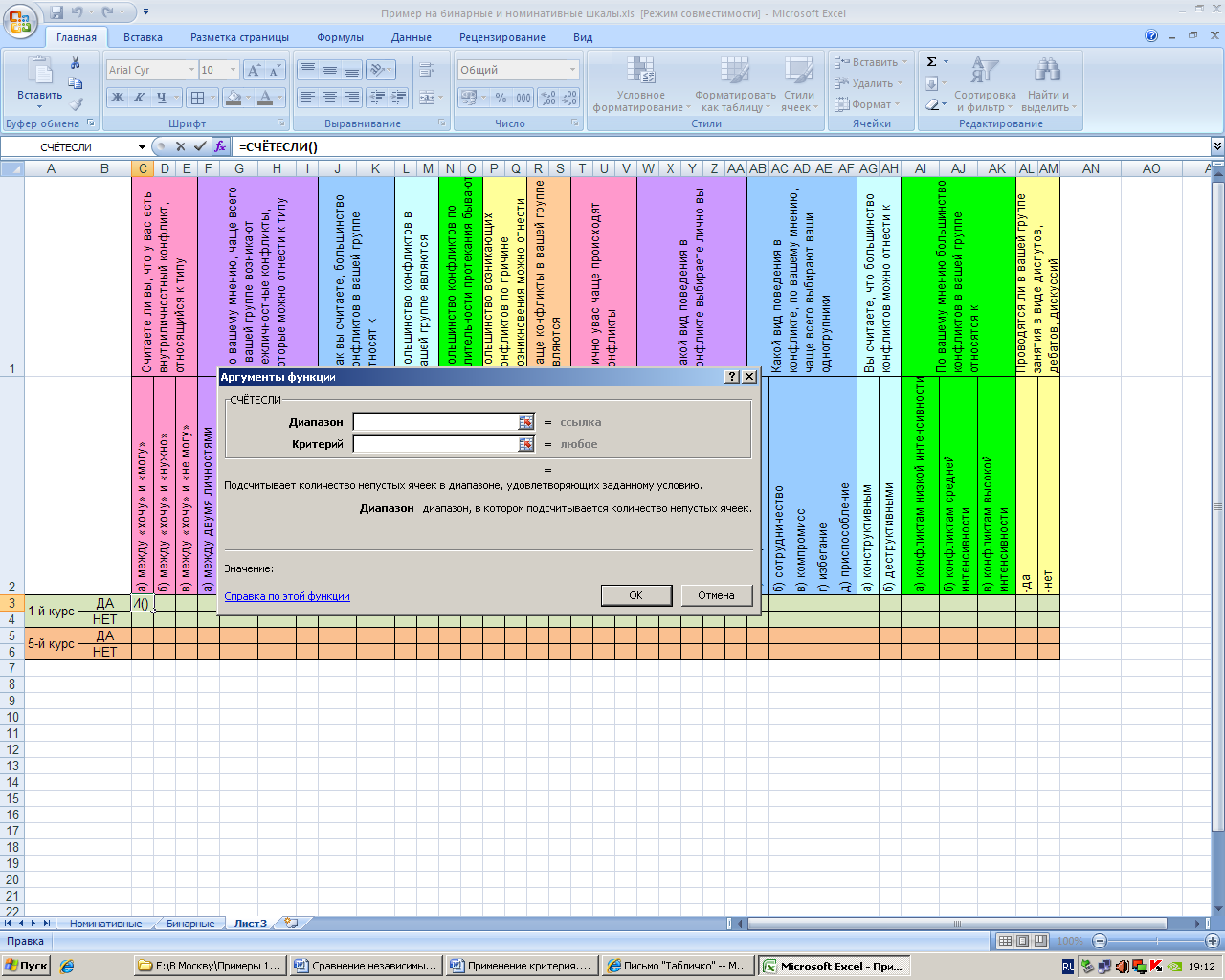
Переходим на лист с исходными данными «Бинарные» и обводим диапазон значений по первому столбцу только для 1-го курса ЯГПУ, критерий устанавливаем равным 1:

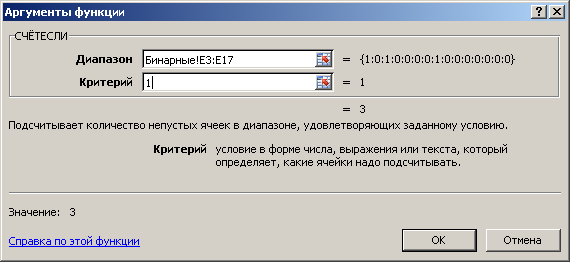
Затем вычислим количество нулей в столбце «а) между хочу и могу» так же только для первого курса ЯГПУ.

Установим курсор в ячейку «Нет, нет конфликта между хочу и могу» и снова вызовем функцию СЧЕТЕСЛИ

Переходим на лист с исходными данными «Бинарные» и обводим диапазон значений по первому столбцу для 1-го курса ЯГПУ, критерий устанавливаем равным 0:

Повторяем вычисления для пятого курса.

В формуле для вычисления хи-квадрат также требуется указать количество всех испытуемых в обеих выборках.

Вычислим это количество, просуммировав полученные значения:

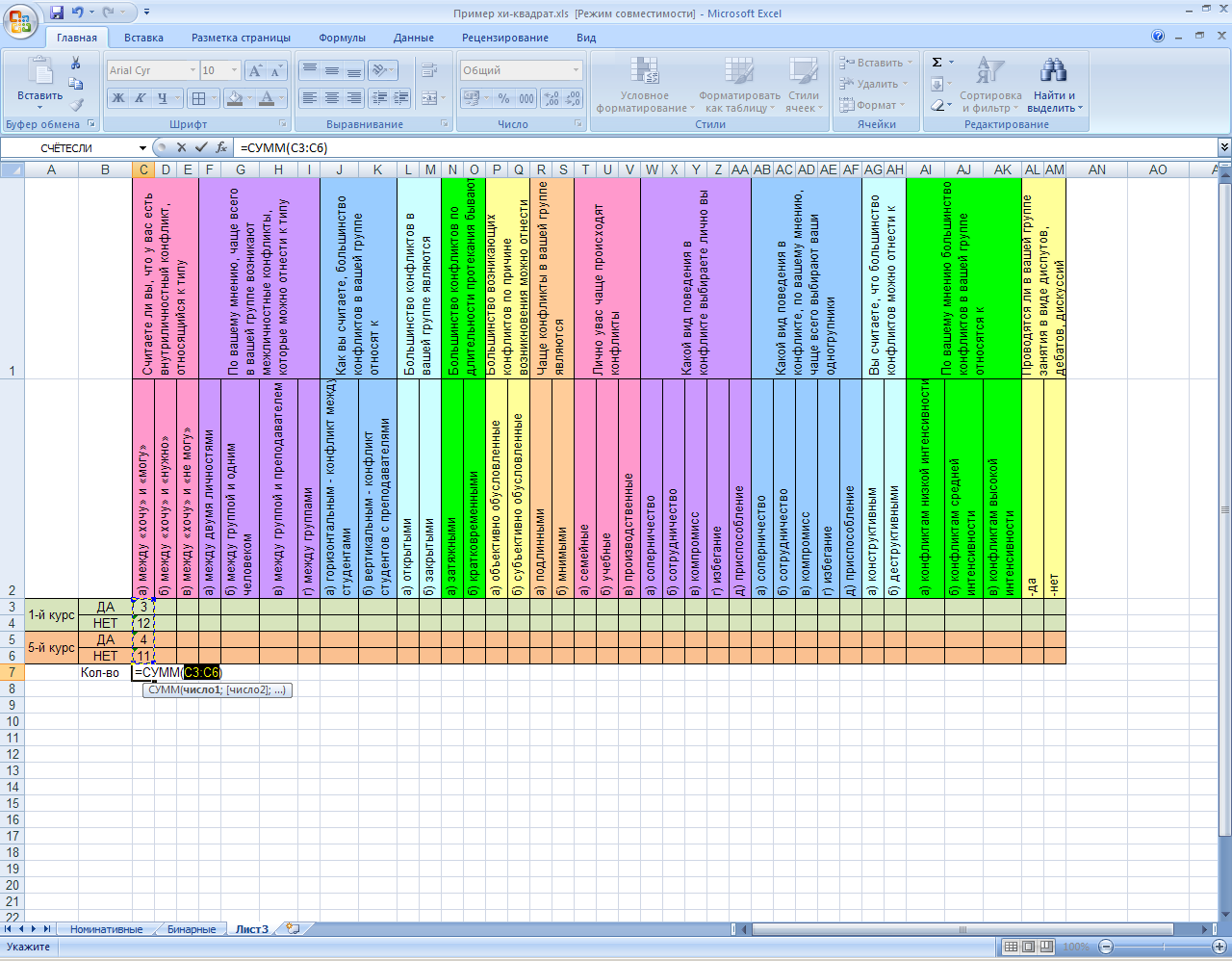
Полученные значения за правый нижний угол «растягиваем» для всех столбцов.

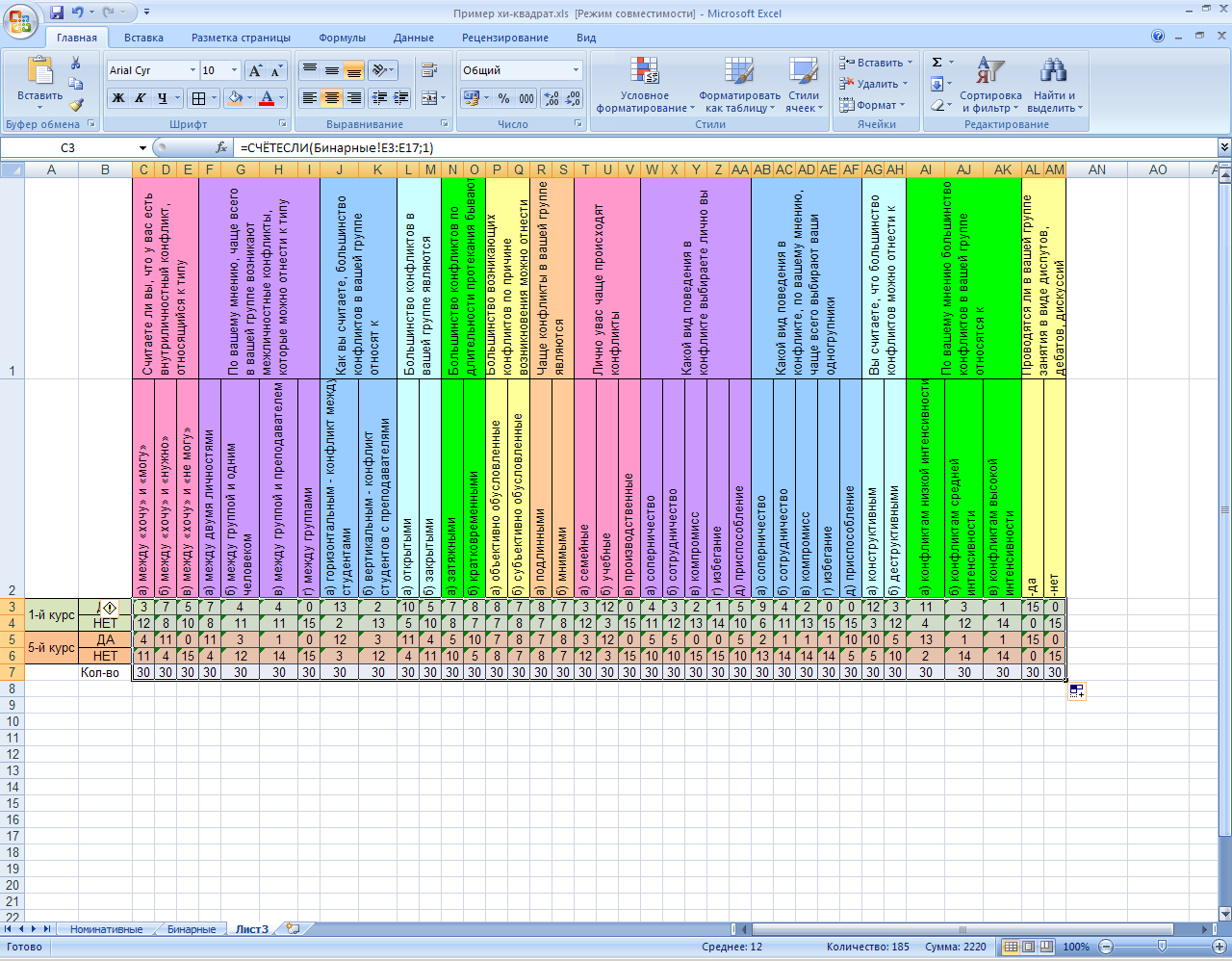
Ели отсутствующих значений нет, количества для всех столбцов будут равны.

Строим формулу для вычисления хи-квадрат для первого столбца:

Для того, чтобы не путать названия ячеек при построении формулы, рекомендуется их подписать:

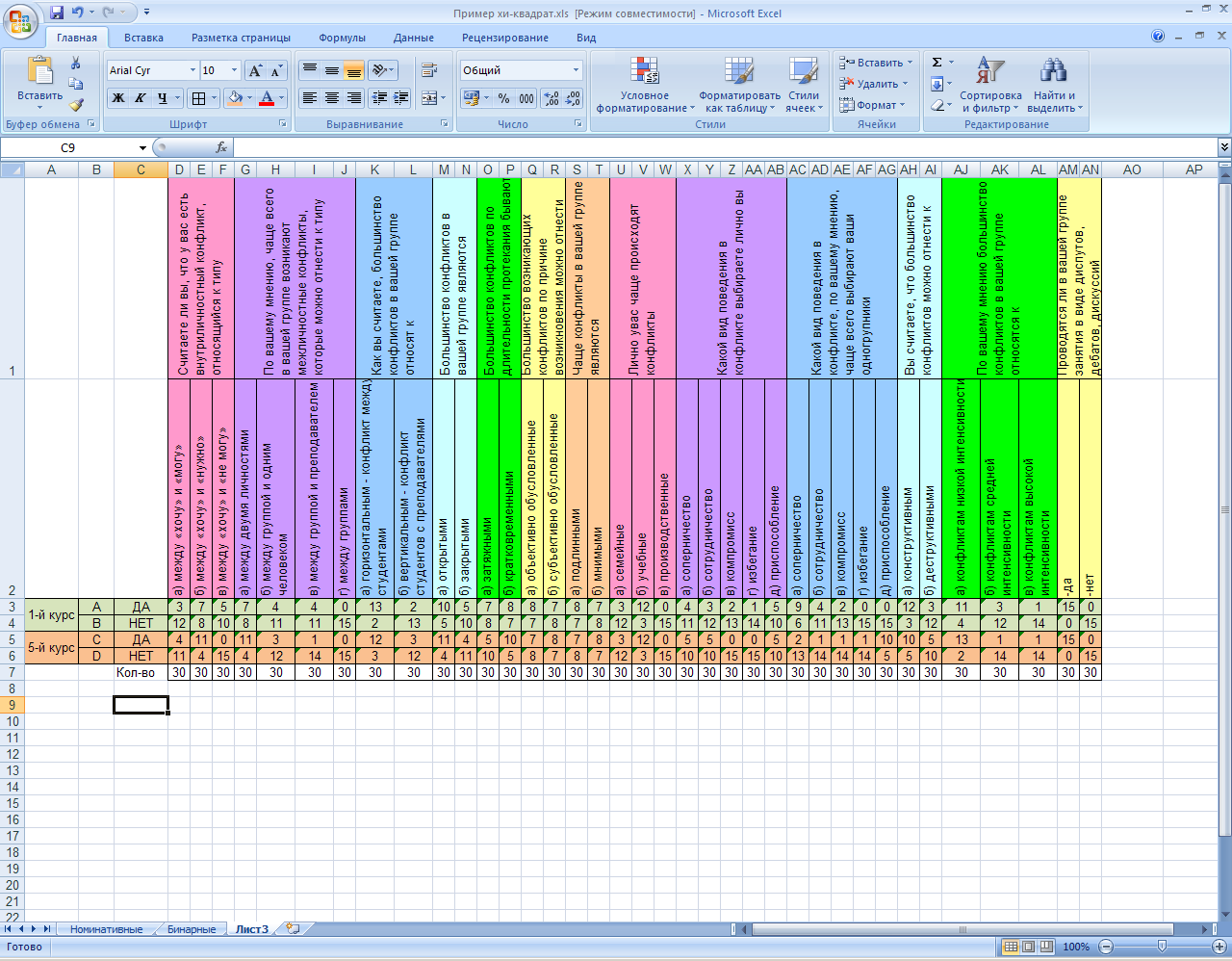
Таким образом, четырехпольная таблица «вытянулась» в один столбец.

Далее строим формулу в том же столбце, относительно которого идет сравнение:

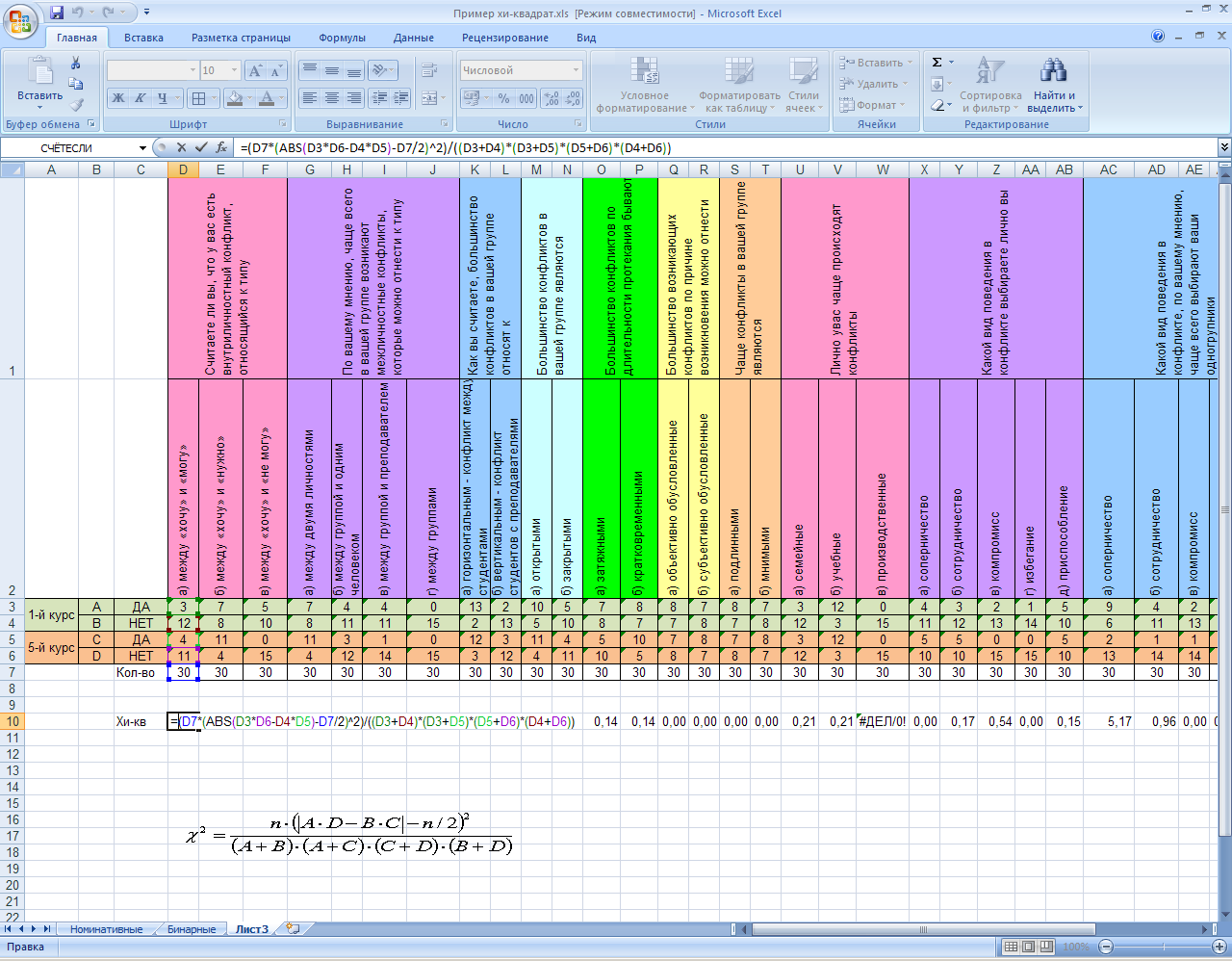
Полученную формулу «растягиваем» на все столбцы.

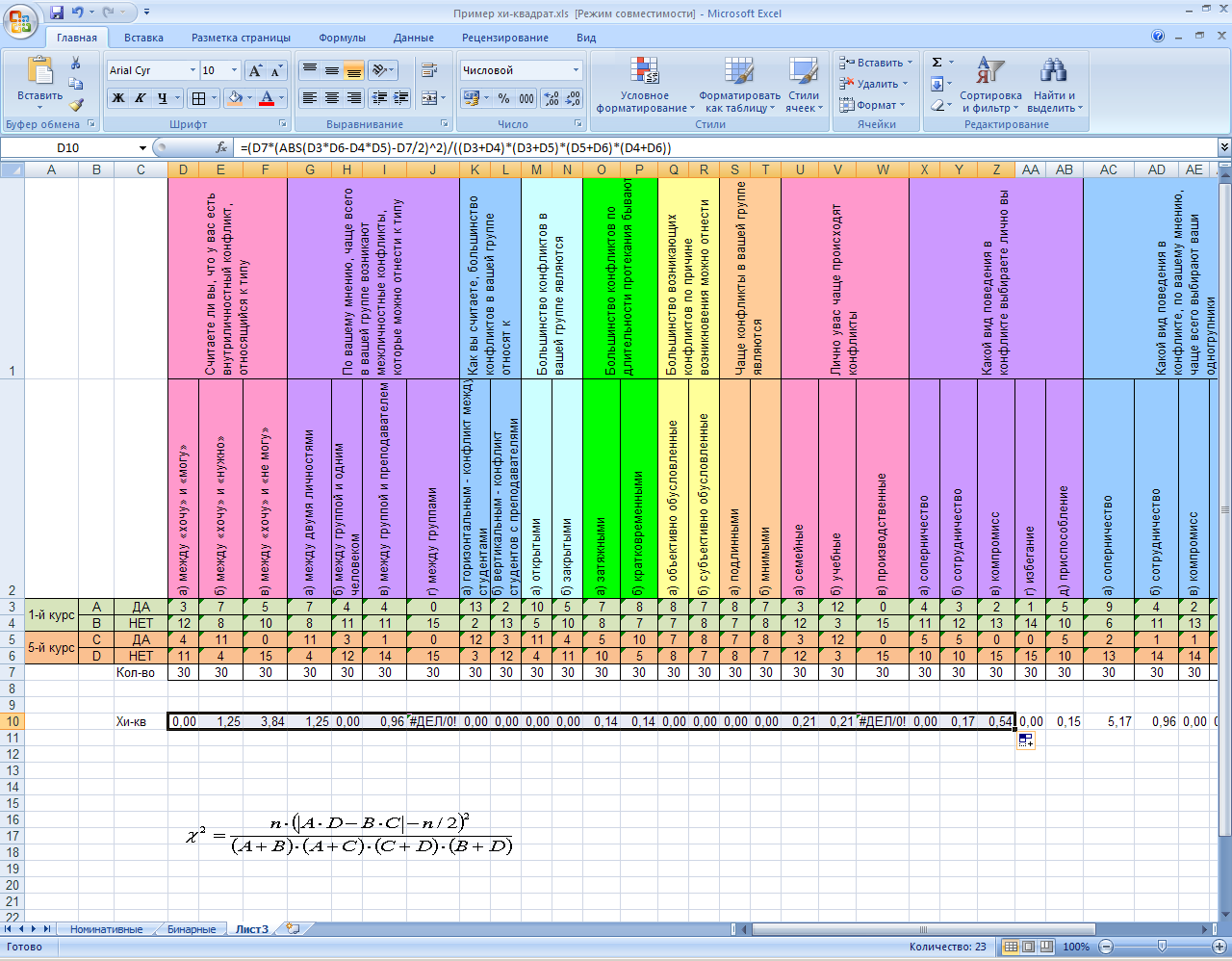
Ячейки, содержащие выражение «ДЕЛ/0» нужно очистить, т.к. это выражение свидетельствует о том, что формула в данном случае неприменима.

Анализ полученных результатов позволяет сделать вывод о том, что статистически достоверно у первокурсников конфликт между «хочу» и «не могу» встречается чаще, чем у пятикурсников (χ²=3,84; p<0,05).

В текстовый документ таблица вставляется, предварительно подготовленная на другом листе. Алгоритм подготовки описан ниже.

Сначала на новый лист переносятся все названия специальной вставкой с транспонированием, далее копируется строка «ДА» для первокурсников и переносится специальной вставкой «значения»+»транспонирование», далее копируется строка «ДА» для пятикурсников и также переносится специальной вставкой «значения»+«транспонирование». Аналогично переносится строка с Хи-квдрат.

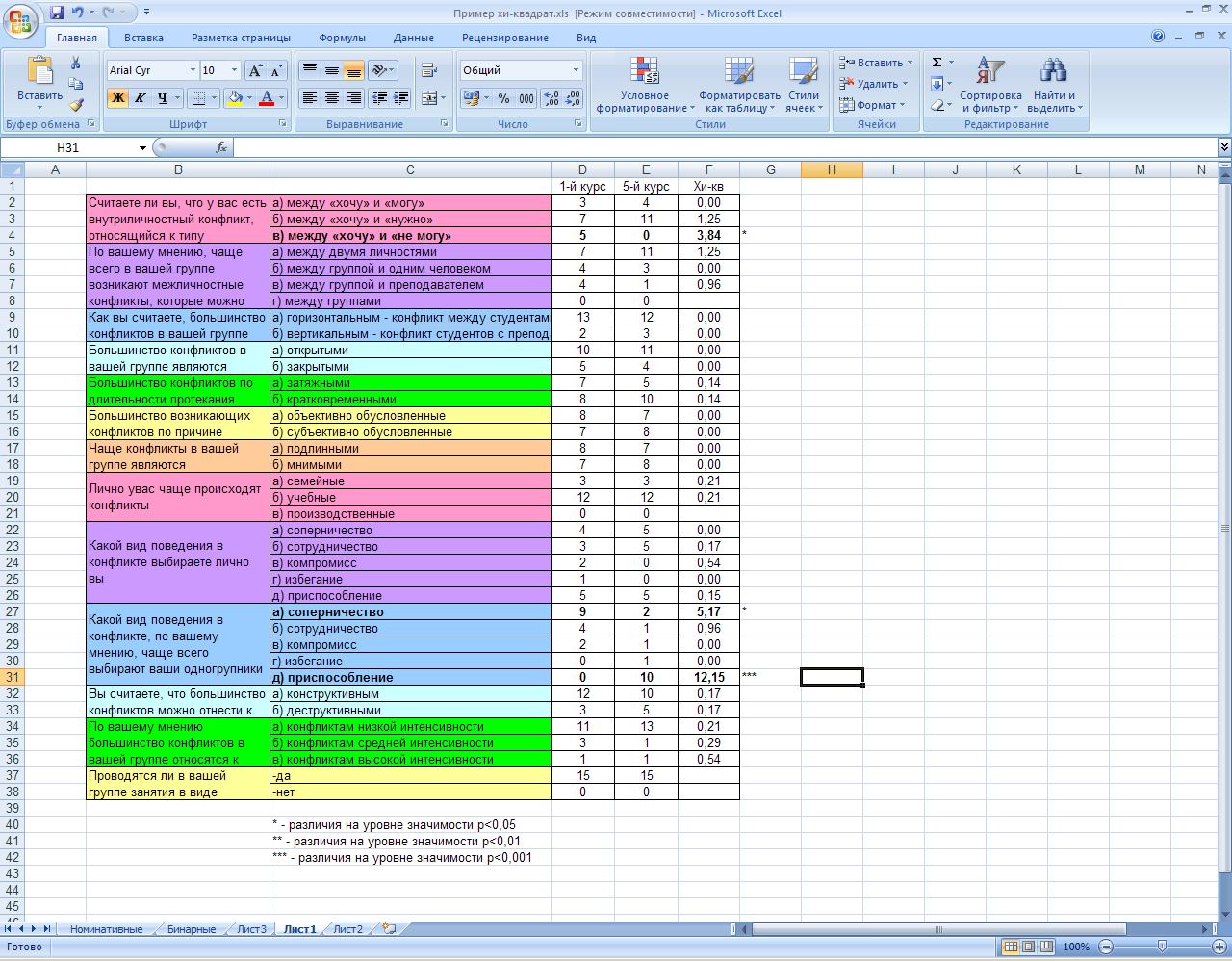
Для более корректного представления результатов количества, приведенные в таблице, также рекомендуется перевести в проценты, т.к. сопоставление долей для выборок неравного объема требует постоянного сопоставления количества испытуемых в сравниваемых выборках, ответивших «ДА» с объемом этих выборок.

Это лучше сделать с использованием расчетной таблицы на предыдущем листе следующим образом:

Сначала вычисляем процент первокурсников, выбравших первый вариант ответа от общего количества первокурсников, выбиравших этот вариант.

Далее построенная формула растягивается вправо на все столбцы.

Для пятого курса формула строится аналогично.

Далее количества в подготавливаемой для переноса в Word таблице заменяются на проценты специальной вставкой «значения»+«транспонирование».

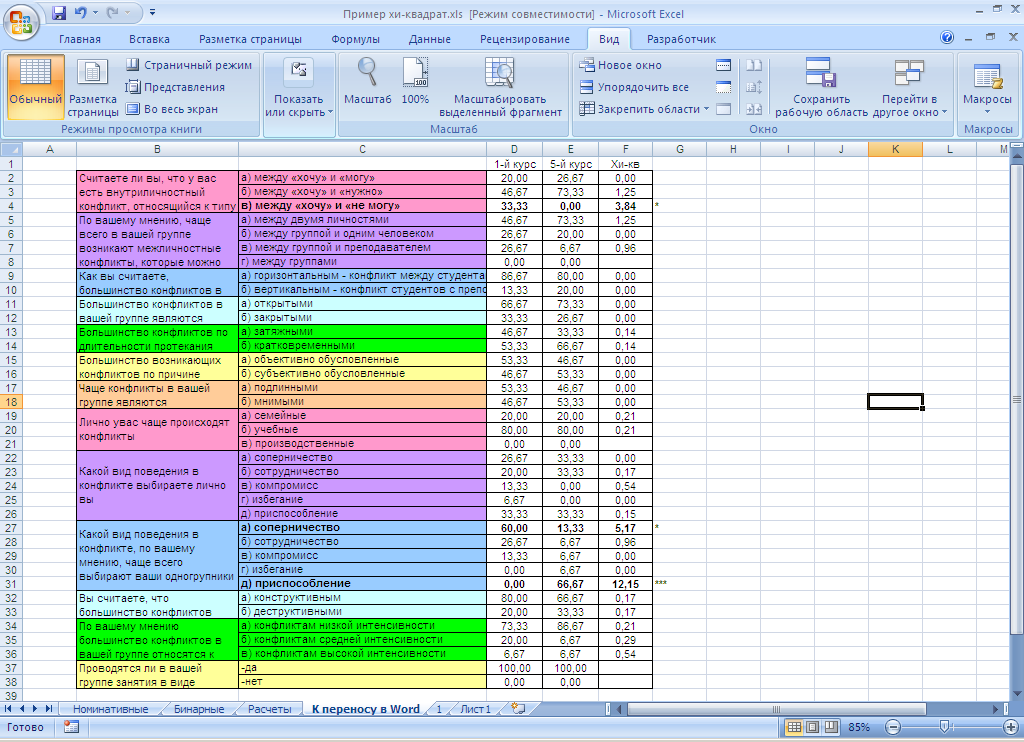
По каждому вопросу анкеты можно построить распределения, обводя соответствующие диапазоны.

Например, на рисунке ниже приведена гистограмма распределения типов внутриличностного конфликта (выбора вариантов на первый вопрос) у первокурсников и у пятикурсников.

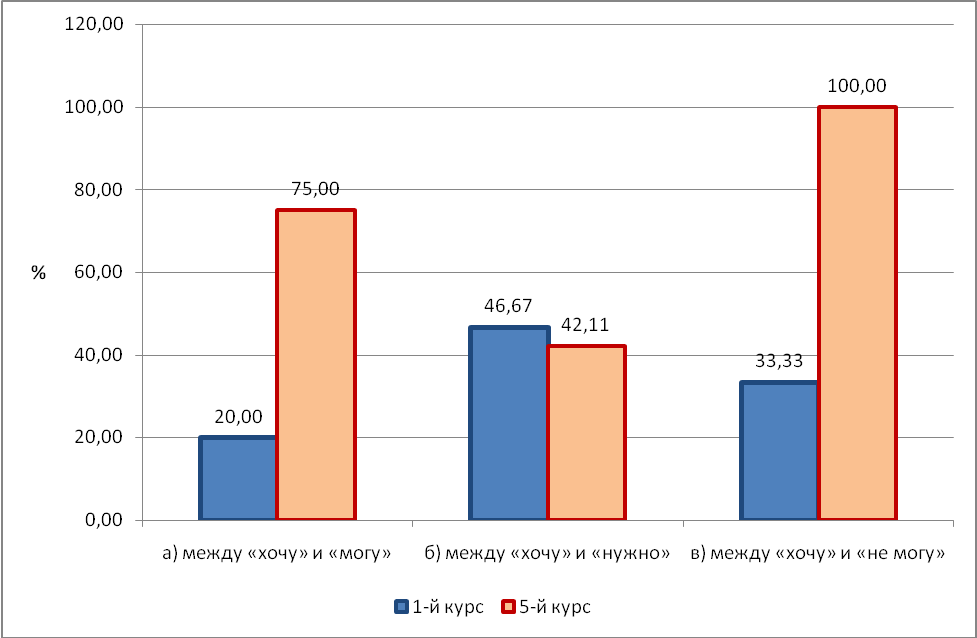
Рис.1. Распределение типов внутриличностного конфликта у студентов 1-го и 5-го курсов.