3.2. Сравнение выборок по u-критерию Манна-Уитни (непараметрический критерий)
Рассмотрим пример сравнения двух выборок.
Подростки |
|||||||||||||||
№ |
Самооценка |
Общая тревожность в школе |
Переживание социального стресса |
Фрустрация потребности в достижение успеха |
Страх самовыражения |
Страх ситуации проверки знаний |
Страх несоответствовать ожиданиям окружающих |
Низкая физиологическая сопротивляемость стрессу |
Проблемы и страхи в отношениях с учителями |
Общий балл тревожнасти |
Соперничество |
Сотрудничество |
Компромисс |
Избегание |
Приспособление |
1 |
9 |
0,05 |
0,36 |
0,15 |
0,5 |
0,17 |
0,2 |
0 |
0,25 |
0,19 |
0 |
0,54 |
0,58 |
0,85 |
0,45 |
2 |
8 |
0,05 |
0,09 |
0,08 |
0,17 |
0,17 |
0,2 |
0 |
0,13 |
0,09 |
0 |
0,62 |
0,67 |
0,54 |
0,64 |
3 |
9 |
0,09 |
0 |
0,08 |
0,33 |
0,33 |
0,2 |
0 |
0,13 |
0,1 |
1 |
0,46 |
0,5 |
0,54 |
0 |
4 |
7 |
0,73 |
0,18 |
0,38 |
0,83 |
0,67 |
0,8 |
0,6 |
0,5 |
0,53 |
0,36 |
0,46 |
0,33 |
0,77 |
0,55 |
5 |
7 |
0,41 |
0,09 |
0,23 |
0,33 |
0,33 |
0,4 |
0 |
0,38 |
0,28 |
0,09 |
0,69 |
0,75 |
0,46 |
0,45 |
6 |
5 |
0,68 |
0,09 |
0,31 |
0,33 |
0,67 |
0,6 |
0,8 |
0,63 |
0,47 |
0,18 |
0,54 |
0,42 |
0,77 |
0,55 |
7 |
8 |
0,09 |
0,18 |
0,08 |
0,33 |
0,17 |
0,2 |
0 |
0,13 |
0,14 |
0 |
0,69 |
0,75 |
0,46 |
0,55 |
8 |
8 |
0,05 |
0 |
0,08 |
0,17 |
0,17 |
0,2 |
0 |
0,13 |
0,07 |
0 |
0,62 |
0,58 |
0,62 |
0,64 |
9 |
8 |
0 |
0 |
0,15 |
0,33 |
0 |
0,2 |
0 |
0 |
0,07 |
0,45 |
0,62 |
0,17 |
0,69 |
0,45 |
10 |
8 |
0,14 |
0 |
0,31 |
0,33 |
0,17 |
0 |
0,2 |
0,5 |
0,16 |
0,64 |
0,31 |
0,5 |
0,77 |
0,18 |
11 |
9 |
0,18 |
0,09 |
0,15 |
0,33 |
0 |
0,2 |
0 |
0,13 |
0,14 |
0,09 |
0,54 |
0,58 |
0,62 |
0,64 |
12 |
8 |
0,59 |
0,36 |
0,31 |
0,67 |
0,67 |
0,2 |
0,2 |
0,25 |
0,41 |
0,45 |
0,54 |
0,67 |
0,31 |
0,55 |
13 |
7 |
0,82 |
0,18 |
0,38 |
0,67 |
0,83 |
0,6 |
0,6 |
0,38 |
0,57 |
0,45 |
0,46 |
0,58 |
0,46 |
0,55 |
14 |
6 |
0,77 |
0,45 |
0,46 |
0,83 |
0,5 |
0,8 |
0,8 |
0,5 |
0,66 |
0,27 |
0,54 |
0,67 |
0,54 |
0,45 |
15 |
9 |
0,5 |
0,09 |
0,15 |
0,5 |
0,67 |
0,6 |
0,4 |
0,38 |
0,36 |
0,36 |
0,31 |
0,67 |
0,62 |
0,55 |
16 |
8 |
0,5 |
0,27 |
0,38 |
0,5 |
0,83 |
0,4 |
0,2 |
0,63 |
0,38 |
0,27 |
0,46 |
0,67 |
0,5 |
0,73 |
17 |
7 |
0,45 |
0,09 |
0,08 |
0,33 |
0,67 |
0,2 |
0,4 |
0,38 |
0,28 |
0,09 |
0,54 |
0,5 |
0,77 |
0,55 |
18 |
8 |
0,55 |
0,09 |
0,38 |
0,5 |
0,83 |
0,8 |
0,6 |
0,5 |
0,43 |
0,36 |
0,69 |
0,67 |
0,31 |
0,45 |
Ср.арифм |
7,72 |
0,37 |
0,15 |
0,23 |
0,44 |
0,44 |
0,38 |
0,27 |
0,33 |
0,30 |
0,28 |
0,54 |
0,57 |
0,59 |
0,50 |
Станд.откл |
1,07 |
0,29 |
0,14 |
0,13 |
0,20 |
0,30 |
0,26 |
0,30 |
0,19 |
0,19 |
0,26 |
0,11 |
0,15 |
0,16 |
0,17 |
Старшеклассники |
|||||||||||||||
№ |
Самооценка |
Общая тревожность в школе |
Переживание социального стресса |
Фрустрация потребности в достижение успеха |
Страх самовыражения |
Страх ситуации проверки знаний |
Страх несоответствовать ожиданиям окружающих |
Низкая физиологическая сопротивляемость стрессу |
Проблемы и страхи в отношениях с учителями |
Общий балл тревожнасти |
Соперничество |
Сотрудничество |
Компромисс |
Избегание |
Приспособление |
1 |
7 |
0,05 |
0,18 |
0,08 |
0 |
0 |
0 |
0 |
0,13 |
0,07 |
0,45 |
0,46 |
0,42 |
0,54 |
0,64 |
2 |
5 |
0,41 |
0,55 |
0,31 |
0,17 |
0,33 |
0,4 |
0,4 |
0,25 |
0,4 |
0,45 |
0,38 |
0,67 |
0,54 |
0,45 |
3 |
6 |
0,14 |
0,09 |
0,23 |
0 |
0,17 |
0,2 |
0 |
0,38 |
0,14 |
0,55 |
0,69 |
0,67 |
0,46 |
0,09 |
4 |
8 |
0,18 |
0,09 |
0,15 |
0,5 |
0,17 |
0 |
0 |
0,38 |
0,17 |
0,09 |
0,62 |
0,58 |
0,54 |
0,64 |
5 |
7 |
0,18 |
0,09 |
0,08 |
0,33 |
0,17 |
0 |
0 |
0,13 |
0,14 |
0 |
0,69 |
0,67 |
0,54 |
0,55 |
6 |
9 |
0,5 |
0 |
0,15 |
0,33 |
0,5 |
0 |
0,4 |
0,38 |
0,28 |
1 |
0,54 |
0,58 |
0,23 |
0,18 |
7 |
8 |
0,27 |
0,45 |
0,46 |
0,33 |
0,17 |
0,6 |
0 |
0,5 |
0,33 |
0,55 |
0,62 |
0,33 |
0,54 |
0,45 |
8 |
9 |
0,18 |
0,45 |
0,46 |
0,17 |
0,33 |
0,2 |
0,4 |
0,38 |
0,31 |
0,36 |
0,46 |
0,67 |
0,62 |
0,36 |
9 |
5 |
0,45 |
0,45 |
0,54 |
0,5 |
0,33 |
0,6 |
0,8 |
0,63 |
0,5 |
0,09 |
0,54 |
0,67 |
0,62 |
0,55 |
10 |
3 |
0,55 |
0,36 |
0,23 |
0,5 |
0,5 |
0,6 |
0,8 |
0,5 |
0,47 |
0 |
0,31 |
0,58 |
0,69 |
0,91 |
11 |
7 |
0,23 |
0,36 |
0,15 |
0,17 |
0,33 |
0,4 |
0 |
0,25 |
0,22 |
0,55 |
0,38 |
0,67 |
0,46 |
0,45 |
12 |
6 |
0,23 |
0,27 |
0,38 |
0,67 |
0,5 |
0,6 |
0,2 |
0,25 |
0,33 |
0,27 |
0,46 |
0,67 |
0,69 |
0,39 |
13 |
9 |
0,09 |
0,27 |
0,15 |
0,33 |
0,17 |
0,2 |
0 |
0,13 |
0,17 |
0 |
0,69 |
0,75 |
0,62 |
0,36 |
14 |
6 |
0,05 |
0,36 |
0,38 |
0,17 |
0 |
0 |
0 |
0,25 |
0,19 |
0,09 |
0,38 |
0,83 |
0,38 |
0,82 |
15 |
3 |
0,32 |
0,36 |
0,46 |
0,17 |
0,33 |
0,8 |
0,4 |
0,5 |
0,34 |
0,27 |
0,31 |
0,75 |
0,54 |
0,64 |
16 |
5 |
0,32 |
0,45 |
0,62 |
0,5 |
0,33 |
0,6 |
0 |
0,63 |
0,22 |
0,27 |
0,46 |
0,42 |
0,54 |
0,73 |
17 |
7 |
0,05 |
0,09 |
0,15 |
0,17 |
0,17 |
0,2 |
0 |
0,25 |
0,1 |
0,55 |
0,77 |
0,33 |
0,38 |
0,45 |
18 |
10 |
0 |
0,55 |
0,46 |
0 |
0 |
0,2 |
0 |
0,5 |
0,22 |
0,45 |
0,46 |
0,5 |
0,46 |
0,55 |
Ср.арифм |
6,67 |
0,23 |
0,30 |
0,30 |
0,28 |
0,25 |
0,31 |
0,19 |
0,36 |
0,26 |
0,33 |
0,51 |
0,60 |
0,52 |
0,51 |
Станд.откл |
2,00 |
0,16 |
0,17 |
0,17 |
0,20 |
0,16 |
0,27 |
0,28 |
0,16 |
0,12 |
0,27 |
0,14 |
0,14 |
0,11 |
0,21 |
Рекомендуется использовать не t-критерий Стьюдента, а его непараметрический аналог U-критерий Манна-Уитни в следующих случаях:
если показатель измерен не по метрической, а по порядковой шкале,
если количество испытуемых в хотя бы одной из выборок меньше 30,
если форма распределения значимо отклоняется от нормальной.
Алгоритм U-критерия Манна-Уитни:
Сравниваемые выборки ранжируют в один общий ряд по возрастанию значений признака, однако записывают их в разные столбцы таблицы.
Каждому элементу ряда присваивают ранг – порядковый номер, указывающий его место в общем ранжированном ряду.
Отдельно для каждой выборки находят суммы рангов R1 и R2
Отдельно для каждой выборки находят величины U1 и U2
Ui = Ri – ni(ni+1)/2.
Выбирают за Uоп меньший из полученных U1 и U2
Находят по таблице (см. Приложение 2) критическое значение Uкр для принятого уровня значимости и объемов выборок n1 и n2.
При Uоп>Uкр делается вывод о том, что статистически значимых различий между выборками не выявлено; при Uоп<Uкр делается вывод о том, что выборки статистически значимо различаются по исследуемому показателю (при этом в тексте указывается значение U и уровень значимости, на котором установлены различия).
Возможности автоматизации вычислений в случае ранговых критериев ограничены, т.к. каждый показатель должен ранжироваться (упорядочиваться по возрастанию) отдельно.
Шаг1. Сначала перенесем на новый лист первый столбец из первой таблицы (самооценка), заливаем его каким-либо цветом, затем переносим такой же столбец из второй таблицы, располагаем его непосредственно ниже первого и красим в другой цвет.
Шаг 2. Для того, чтобы упорядочить значения самооценки по возрастанию, сначала выделяем их (только числа!), затем выбираем в Главном меню пункт «Данные», далее «Сортировка» от А до Я (по возрастанию).
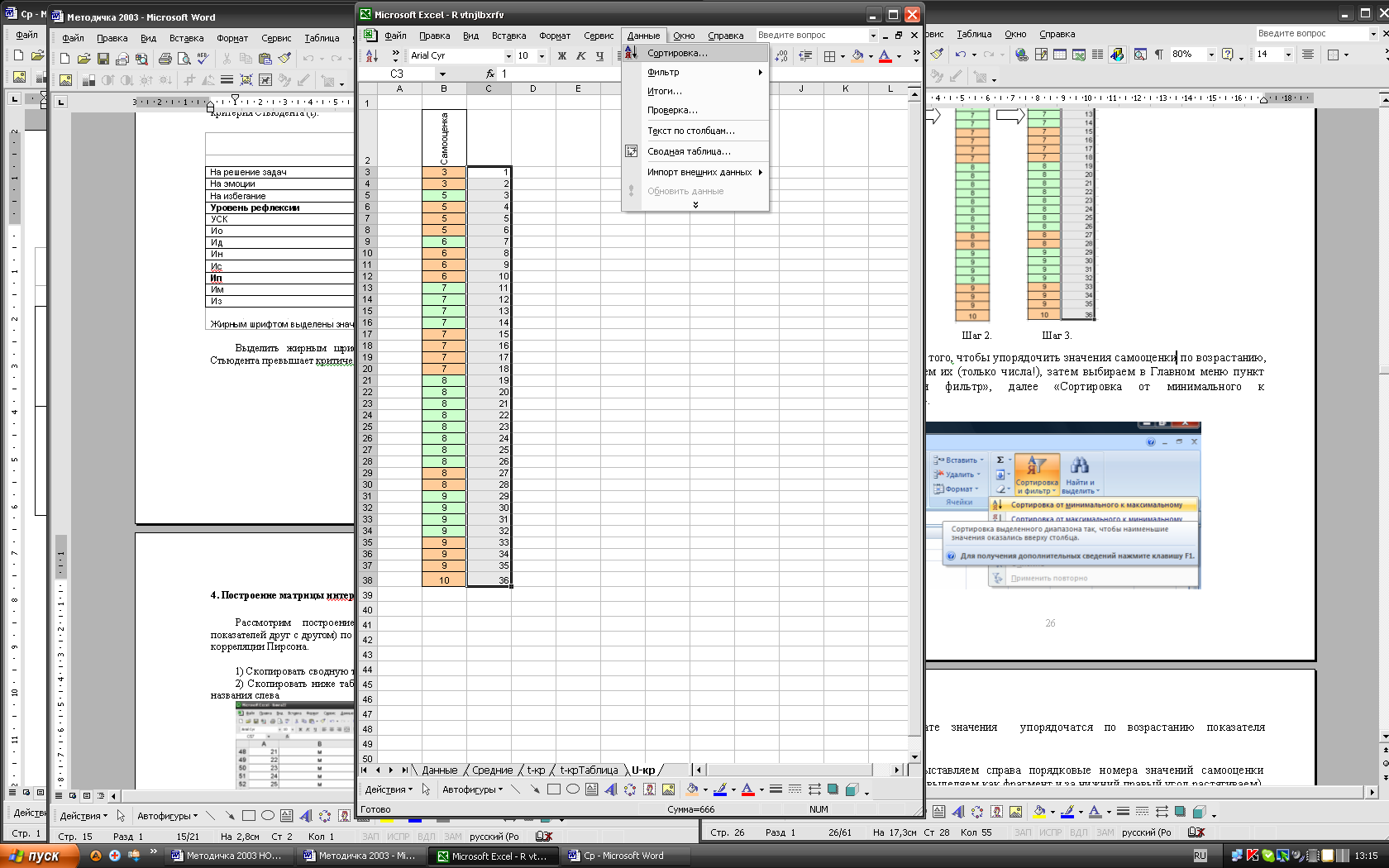
В результате значения упорядочатся по возрастанию показателя «Самооценка».
Шаг 3. Выставляем справа порядковые номера значений самооценки (набираем 1 и 2, выделяем как фрагмент и за нижний правый угол растягиваем).
Шаг 4. При помощи форматирования по образцу (желтая кисточка в Главном меню) копируем формат со значений самооценки на их порядковые номера. Для этого выделяем мышкой все значения самооценки, нажимаем на значок желтой кисточки на панели инструментов и обводим мышкой все порядковые номера.
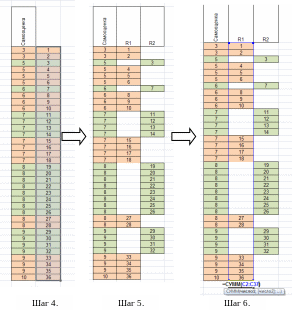
Шаг 5. Далее порядковые номера одной из выборок (например, первой) «отодвигаем» вправо на одну ячейку. Получается два частично заполненных столбца, в каждом – свой цвет. Обозначаем их как R1 и R2.
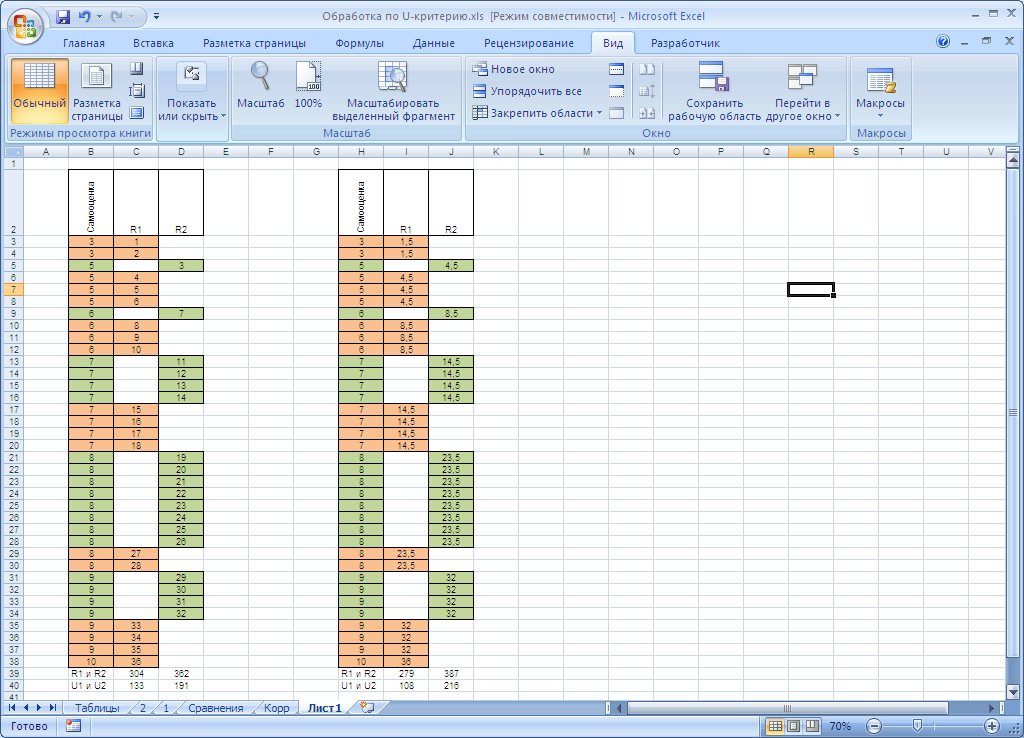
Шаг 6. Далее высчитываем суммы по столбцам R1 и R2, пользуясь функцией суммирования и обводя весь диапазон.
Шаг 7. Вычисляем U1 и U2 по формуле, где n1 и n2 – объемы первой и второй выборок.
Шаг 7.
Шаг 8.
Шаг 8. Из двух вычисленных U выбираем меньший и сравниваем с критическим значением U сначала для р=0,05, а потом, если вычисленное U окажется меньше – с критическим значением U для p=0,01 из таблиц в Приложении 2. Критические значения находим на пересечении n1 и n2 – объемов сравниваемых выборок. В нашем примере n1=18 и n2=18. Поэтому U0,05(18;21)=99 и U0,01(18;21)=81.
Так как меньшее из вычисленных значений U1=133 больше критического U0,05(18;21)=81, то можно сделать вывод о том, что уровень самооценки у подростков и у старшеклассников статистически значимо не различается.
Вышеприведенный алгоритм вычисления U-критерия является приближенным. В статистических пакетах реализован более точный алгоритм, построенный на связанных рангах.
Шаг 9. Чтобы преобразовать наш результат в соответствии с более точным алгоритмом, нужно заменить порядковые номера у совпадающих значений показателя на средние арифметические по этим порядковым номерам:
Шаг 9.
Как видим, вычисленное значение U=108, что отличается от предыдущего значения.
Для ускорения вычислений среднего арифметического можно воспользоваться встроенной функцией СРЗНАЧ(), обводя в качестве диапазона все порядковые номера совпадающих значений.
Например, для вычисления среднего арифметического порядковых номеров значения «8» нужно установить курсор в любую свободную ячейку, вызвать функцию СРЗНАЧ() и при указании диапазона обвести все порядковые номера, соответствующие этому значению.
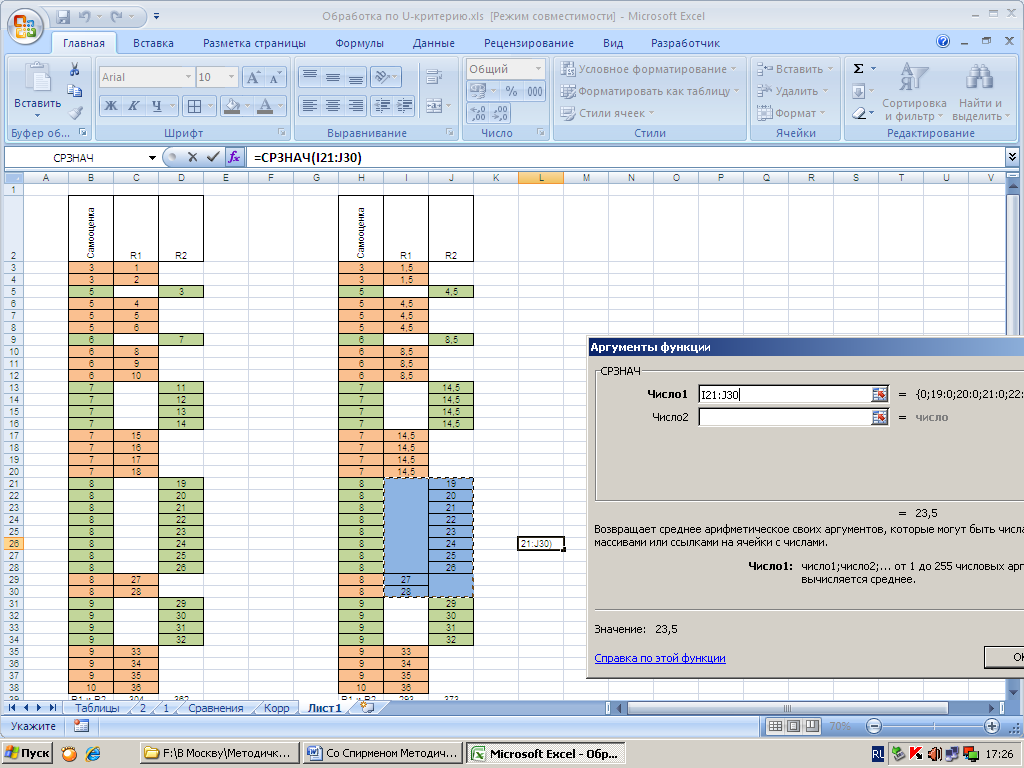
Далее нужно заменить все порядковые номера «8» на полученный результат 23,5.