9. Кодирование информации

Поскольку в информатике мы рассматриваем информацию как результат обработки данных адекватными методами, возникает вопрос о представлении данных. Сразу надо отметить, что за основу мы будем принимать дискретную форму представления сообщений, принятую в информатике.

Человечество давно решило эту проблему. Любое общение между людьми происходит именно благодаря тому, что они научились выражать образы, чувства и эмоции с помощью специально предназначенных для этого знаков и сигналов — звуков, жестов, букв и пр. Процесс представления информации в виде знаков называют кодированием. Одну и ту же информацию мы можем выразить разными способами.

Как отмечалось, за основу принят так называемый алфавитный способ представления информации. Дискретные сообщения представляют собой (конечные или бесконечные) последовательности знаков некоторого алфавита. При этом, исходя из соображений, связанных с физиологией органов чувств, или из чисто технических соображений, их обычно разбивают на конечные последовательности знаков, называемые словами.

Принято говорить, что если алфавит избран или зафиксирован, то слова строятся “над” этим алфавитом. Слова над двоичным набором знаков называются двоичными словами. Они не обязаны иметь постоянную длину азбука Морзе, например: A = • ─, S = •••, но если это так, т. е. все слова имеют длину n, то говорят об n-разрядных словах или кодах. Например, восьмиразрядный код ASCII.

Возникает вопрос, а если одна и та же информация представлена над разными алфавитами? На оживленном перекрестке регулировщик помогает избежать аварии с помощью жестов. В тоже время его жесты соответствуют определенным сигналам светофора. Просто, необходимо знать правило, по которому каждому знаку одного алфавита ставятся в соответствие знаки другого алфавита. Ясно, что при разной длине алфавитов взаимно однозначным соответствием здесь не обойтись, знаков одного из алфавитов может не хватить. В таком случае знакам одного алфавита ставятся в соответствие комбинации знаков другого алфавита, т. е. слова другого алфавита. Чаще всего при этом используются слова постоянной длины. Правило, устанавливающее соответствие называется правилом кодирования, или кодом.

Дадим точное определение.

Кодом называется правило, описывающее отображение одного набора знаков в другой набор знаков; также называют и множество образов при этом отображении. То есть термин «код» используется в двух смыслах — как правило кодирования и как множество, состоящее из наборов знаков, т.е. слов используемых для кодирования

Длина используемых слов так же называется еще длиной кода.

Код (фр. code — кодекс, свод законов). Начиная с середины XIX века это слово, помимо основного значения, означало книгу, в которой словам естественного языка сопоставлены группы цифр или букв.

Коды с постоянной длиной кодовых слов использовать технически проще, так как слова могут следовать друг за другом без делителей. Исходная группировка кодовых слов устанавливается с помощью отсчета.

Наиболее простым для кодирования является двоичный алфавит. Чем меньше знаков в алфавите, тем проще должна быть устроена «машина» для распознавания (дешифровки) информационного сообщения. Однако чем меньше знаков в алфавите, тем большее их количество (большая длина кода) требуется для кодирования информации. В качестве двоичного алфавита мы могли бы использовать, например такой {∆,}, но без особого напряжения воображения можно согласиться с применением известных нам арабских цифр {0,1}. Несложный подсчет показывает, что при длине кодового слова равной двум мы сможем закодировать 4 символа другого алфавита. Приведем одно из возможных объяснений. В каждой из 2-ух позиций может стоять один из 2-х знаков алфавита. Для первой позиции существует 2 возможности. Для каждой из этих возможностей рассмотрим 2 возможности для второй позиции, — всего будем иметь 2*2 = 4 возможностей, другими словами можем закодировать 4 символа. Рассуждая аналогично для случая, где длина слова равна трем, получим 2*2*2=2³ возможностей, т.е. 8 слов. Обобщая, можно сделать вывод. При длине слова равной n знаками двоичного алфавита можно закодировать 2ⁿ различных состояний или символов. Если имеется алфавит, состоящий из k знаков, то в этом случае можно закодировать kⁿ различных состояний.

Итак, если алфавит состоит из k знаков и используется код с постоянной длиной п, то можно закодировать М = kⁿ различных состояний.

В вычислительной технике в настоящее время широко используется двоичное кодирование с алфавитом {0,1}. Наиболее распространенными кодами являются ASCII (American standard code for information interchange — американский стандартный код для обмена информацией), ДКОИ-8, Win 1251.

Передача сообщений всегда осуществляется во времени. Процесс кодирования также требует определенного количества времени, которым зачастую нельзя пренебрегать. При кодировании могут ставиться определенные цели и применяться различные методы. Наиболее распространенные цели кодирования:

• экономность (уменьшение избыточности сообщения, повышение скорости передачи или обработки);

• надежность (защита от случайных искажений);

• сохранность (защита от нежелательного доступа к информации);

• удобство физической реализации (двоичное кодирование информации в ЭВМ);

• удобство восприятия (схемы, таблицы).

Методы кодирования могут быть различными, так, например, при двоичном кодировании строят двоичное дерево. Из единого корня (узла) движение налево обозначают знаком 0, а движение направо – знаком 1. Доходя до первого узла, поступают аналогичным образом и так далее. При наличии у дерева 3-х узлов, каждой из восьми цифр от 0 до 7 можно сопоставить свой 3-хзначный двоичный код. См. рис.№ , из которого видно, что 0 соответствует 000, 1 – 001, … , 7 – 111.

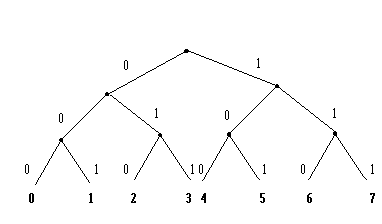
Рис. 5

Знание кодирования информации позволяет нам представлять ее в виде сообщения над некоторым алфавитом. Сообщение это всегда некоторая форма преставления информации. Однако следует различать сообщение и заключённую в нём информацию (смысл сообщения для источника и получателя). Одна и та же последовательность сигналов может нести для разных получателей различную информацию.