3. Носители информации. Знаки и сигналы

Какой бы мы позиции на происхождение информации ни придерживались, прежде чем оперировать информацией, ею надо располагать. Распространение же информации всегда связано с материальным носителем, то есть средой для её записи, хранения, передачи.

Носителем информации может быть:

• любой материальный предмет (бумага, камень, дерево, стол, классная доска, звездная пыль);

• волны различной природы: акустическая (звук), электромагнитная (свет, радиоволна), гравитационная (давление, притяжение):

• вещество в различных состояниях (жидкий раствор — информацией может быть, в частности, концентрация молекул; газ — информацией в этом случае могут являться его температура и давление

В соответствии с избранным носителем, технические устройства передачи информации могут работать используя механическое движение, давление жидкостей и газов (гидравлика и пневматика), электрические напряжения и токи, свободные электромагнитные волны (от 10² кГц до 10⁶ МГц), пучки электромагнитных волн (светосигнальная аппаратура, лазеры).

Для хранения информации, которая будет обрабатываться с помощью компьютера, используются специальные машинные носители информации: электронные схемы, перфокарты (использовались раньше), магнитные ленты, магнитные диски, оптические компакт-диски и т. п.

Каким же образом представляется информация на носителях той или иной природы? Имеются ли отличия в формах представления информации в зависимости от природы носителя. Что имеется общего и каковы отличия?

Человек всегда стремился доступным ему способом зафиксировать сведения о том, что больше всего его волновало. Наши давние предки оставили нам информацию о себе в виде наскальных росписей. Отсюда и произошло идеографическое письмо, в основу которого положены идеограммы — письменные знаки (условное изображение или рисунок), соответствующие не отдельным звукам, а словам или словосочетаниям.

Позже информация о волнующих людей событиях наносилась на поверхности искусственных, как правило, монументальных сооружений, которые донесли ее до наших дней (гробницы, стелы, ритуальные сооружения). Однако монументальные сооружения не были транспортабельны. Чтобы получить необходимую информацию, которая там хранилась, люди были вынуждены совершать путешествия к этим сооружениям. Это было крайне неудобно. Постепенно формировалось понятие знака, как представление объекта, он стал играть все возрастающую роль, возникали предпосылки возникновения письменности.

В то же время люди использовали звук и свет для передачи сообщений на расстоянии. Свет костра, звук барабана несли определенную информацию для человека. Изменение цвета листьев комнатного цветка, их поникший вид сигнализируют о необходимости позаботиться о поливе и подкормке растения.

Итак, можно констатировать, что в ходе исторического развития человек научился передавать и сохранять информацию с помощью знаков и сигналов, именно они становятся основными формами передачи и хранения информации в социотехнических системах.

Чтобы подчеркнуть, что носителем информации является физический предмет (лист бумаги, классная доска, камень, картина) с какими-либо изображениями на нем, говорят, что информация записана в виде знаков. А если носителем информации является волна или вещество, то говорят, что информация переносится в виде сигналов.

Как мы уже отмечали в процессе энергообмена и переходов энегии из одной формы в другую появляются сигналы. Процессы эти разворачиваются во времени, поэтому в качестве носителей информации заслуживают внимания такие физические величины, которые изменяются во времени, а это чаще всего связано либо с волнами, либо с веществом. В этой связи сигналом мы называем изменение некоторой физической величины во времени, обеспечивающее передачу информации. Та характеристика, которая используется для представления сообщения, называется параметром сигнала.

Не обязательно, чтобы физически различные значения выбранного параметра соответствовали различной информации.

Однако, следует отметить, что сигналы, передаваемые в электрической форме (электромагнитные волны), обладают множеством достоинств:

1) не требуют движущихся механических устройств, медленных и подверженных поломкам;

2) скорость передачи электрических сигналов приближается к максимально возможной скорости — скорости света;

3) электрические сигналы легко обрабатывать, сравнивать и преобразовывать с помощью электронных устройств, отличающихся чрезвычайно высоким быстродействием.

Наполнение знаков и сигналов смыслом превращает их в символы. Символ — это знак или сигнал, наполненный смыслом.

Сигналы могут быть непрерывными (аналоговыми) или дискретными.

Аналоговый сигнал — сигнал, параметр которого непрерывно изменяется во времени (температура воздуха, сила тока, напряжение, скорость движения), и фактически представляется функцией y(t), принимающей любые вещественные значения в диапазоне изменения аргумента t . При этом функция y(t) передает характер изменения процесса во времени.

Аналоговые сигналы используют, например, в телефонной связи, радиовещании, телевидении.

Сигнал называется дискретным, если параметр сигнала может принимать лишь конечное число значений (дискретный — не непрерывный).

Дискретные сигналы	Аналоговые сигналы
Цвет светофора Цифры, буквы, слова Знаки дорожного движения Телеграфная азбука Морзе	Скорость автомобиля Влажность воздуха Пение и игра на музыкальных инструментах Кардиограмма

Сигнал, несущий информацию, должен принимать, по крайней мере, два различных значения (в его простейшей форме), но не менее. Не бывает информационного сигнала, принимающего только одно значение.

Пример. На сторожевой башне огонь означает «опасность», огня нет — «все спокойно».

В реальной жизни мы чаще всего воспринимаем непрерывные сигналы. Даже речь человека, по сути, представляет собой непрерывный сигнал. В этом легко убедиться, если вспомнить, что речь на незнакомом языке воспринимается слитно, в ней трудно выделить отдельные слова. Но дискретные сигналы обрабатывать легче. Благодаря сложившейся с детства привычке, мы выделяем в сигналах, непрерывно поступающих к нам из внешнего мира, отдельные элементы: лица и облака, слова и музыкальные фразы. Этот процесс называется дискретизацией непрерывного сигнала. Выделяя отдельные элементы сигнала, мы ставим им в соответствие знаки. При этом, чаще всего применяется так называемый алфавитный способ. Выбирается некоторый конечный набор различающихся между собой знаков одной природы, называемый алфавитом. При этом трактовать алфавит можно самым расширительным образом, допуская в качестве него и набор графем (знак письма), и знаков зодиака, и, даже, кивки головой.

Следует отметить, что в целях удобства применения алфавит наделяют линейным порядком. Знак же – это элемент некоторого конечного множества отличимых друг от друга “вещей”, набора знаков.

Примеры алфавитов (порядок в них – это порядок перечисления):

1. алфавит десятичных цифр {0,1,2,3,4,5,6,7,8,9};

2. алфавит знаков зодиака

3. алфавиты заглавных латинских букв {A,B,C,D,E,F,G,H,I,J,K,L,M,N,0,P,Q,R,S, T,U,V,W,X,Y,Z};

4. алфавиты заглавных букв кириллицы, а так же других национальных алфавитов {А, Б,В,Г,Д,Е,Ё,Ж,З,И,Й,К,Л,М,Н,О,П,Р,С,Т, У,Ф,Х,Ц,Ч,Ш,Щ,Ъ,Ы,Ь,Э,Ю,Я};

5. набор знаков планет

Дискретные сообщения представляют собой конечные последовательности знаков, при этом, исходя из соображений, связанных со строением органов чувств, или из чисто технических соображений, их обычно разбивают на конечные последовательности знаков, называемых словами. Каким образом это происходит, мы рассмотрим в одном из последующих параграфов, касающихся кодированию. Здесь же рассмотрим процесс дискретизации более подробно.

Рассмотрим сообщение, которое надо дискретизировать, абстрактно – как непрерывную вещественную функцию, заданную на конечном интервале. Наглядно такую функцию можно представить кривой – ее графиком. Иллюстрация представлена на рис. 2.

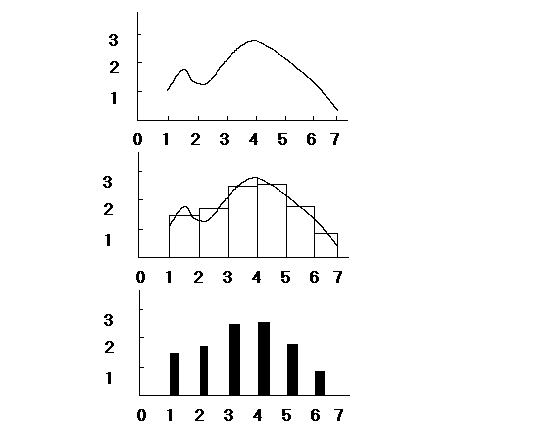
Рис. 2. Развертка, этапы

Процесс дискретизации пойдет в два этапа: развертки и квантования. Развертка состоит в том, что область определения функции разбивается на подинтервалы равной длины. У нас выбрана единичная длина, хотя это вовсе не обязательно. Сама функция заменяется другой, которая постоянна на каждом подинтервале, причем в качестве значения в нем берется некоторое среднее значение, но могут быть выбраны максимальное или минимальное или какое-то другое значения. Тем самым исходная функция аппроксимируется соответствующей ступенчатой функцией. Ступенчатую функцию часто изображают посредством последовательности равноотстоящих друг от друга вертикальных линий, высота которых задает среднее значение. Получающийся при этом график называют пульсом. Таким образом, развертка состоит в замене функции ее пульсом. Средние значения могут быть получены с помощью простого усреднения, либо в качестве среднего берется значение функции в определенной точке интервала, например, в его середине. Чем грубее развертка, то есть чем больше шаг разбиения, тем больше свойств исходной функции теряется.

Таким образом, развертка есть этап, преобразующий функцию в последовательность ее значений. Значения функции заполняют обычно некоторый континуум вещественных чисел, именно – это те значения, которые может принимать физическая величина – параметр сигнала. В противоположность этому дискретное сообщение – это конечная последовательность знаков. В общем случае значение функции на интервале является вещественным и даже иррациональным числом. Так у нас на рисунке, на первом интервале, значением функции является смешанная десятичная дробь. Чтобы упростить форму представления значений функции выполняют следующий этап – квантование. Квантование осуществляет переход от вещественных значений функции к дискретным сообщениям.

Квантование – это отображение вещественных чисел в некоторое счетное множество чисел, а именно в множество всех кратных некоторого числа ∆, называемого шагом квантования. Отображение устроено так, что всякий из наших равных по длине интервалов чисел отображается в то кратное ∆, которое лежит в этом интервале. В случае, представленном на рис. 3, шаг квантования 1 и все числа интервала [0,5; 1,5] отображаются в единицу, следующего интервала в двойку, и так далее. Квантование переводит значения функции в конечное множество чисел, которое можно понимать как набор знаков. Таким образом, развертка и последующее квантование дают последовательность знаков – произвольное сообщение превращается в дискретное слово над некоторым набором знаков.

Квантование по середине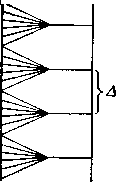

4,5

3,5

2,5

1.5

0,5

4

3

2

1

Рис 3

Для функций многих переменных с многомерной областью определения, графические изображения дискретизируются в соответствии с матричным принципом. Первое представление об этом принципе дает следующая схема действий: на имеющийся рисунок как бы наносится сетка и просматривается клетка за клеткой этой сетки. Если изображения в клетке нет, то ей в соответствие ставится, например, 0, если изображение в клетке есть — ставится.