23. Эвристический подход, понятие "жадного" алгоритма, пример решения задачи коммивояжера, алгоритм Крускала

Очень часто для решения np-задач используют эвристический подход. Алгоритмы, которые быстро находят подходящее, но не оптимальное решение, называются эвристическими.

Примером рационального эвристического алгоритма служит "жадный" алгоритм. Каждый алгоритм действует, используя в данный момент лишь часть исходных данных и принимая полученное решение на основе этих данных. Далеко не каждый "жадный" алгоритм обеспечивает оптимальное решение.

Задача коммивояжера.

Задан набор городов. Определить порядок городов, посетив каждый город лишь один раз и вернуться в начальный (чтобы путь был минимальным).

S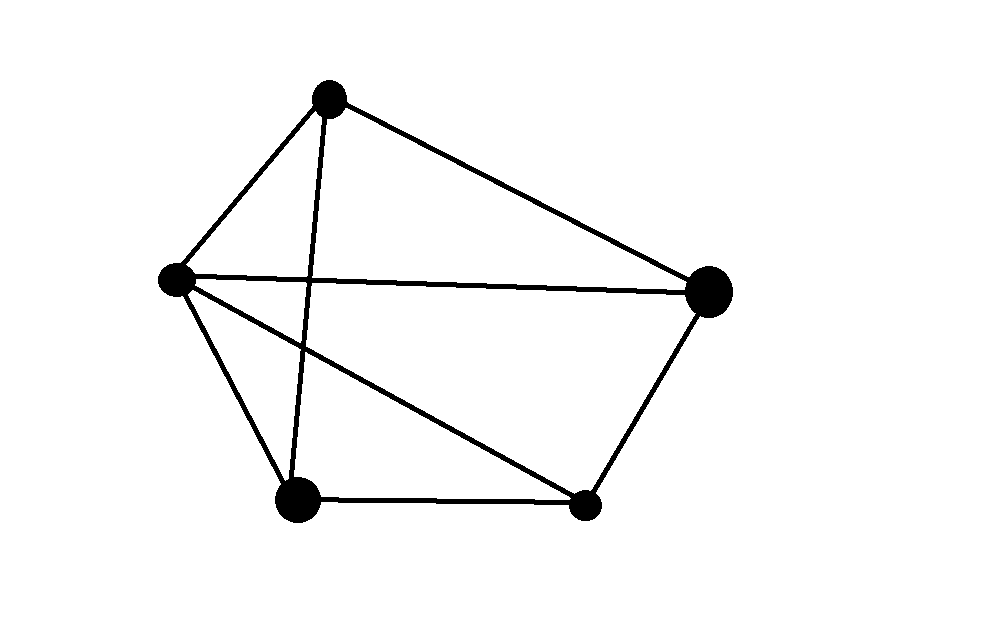 (n) - min

n=8 городов, 8!=40320

n=10 городов, 10!=3628800

Предположим, что есть алгоритм подсчета стоимости путешествия. На путь через 15 городов уйдет 40 лет. Для 20 городов 100 миллионов компьютеров должны будут работать параллельно 9 месяцев.

Переборный вариант этой задачи относится к классу 0(n!). Будем заниматься поиском путей решения таких задач. Существует два подхода для решения задачи коммивояжера:

1. Дейкстры-Прима (основан на рассмотрении вершин графа)

2. Крускала (делает упор на ребра графа).

Начинаем с пустого графа и добавляем ребра в порядке возрастания их весов, пока не получим набор ребер, объединяющих все вершины.

Условия:

1. Ребро принимается в том случае, если оно не образует цикл с уже принятыми ребрами.

2. Ребро принимается, если это не приводит к появлению вершины со степенью 3 и более.

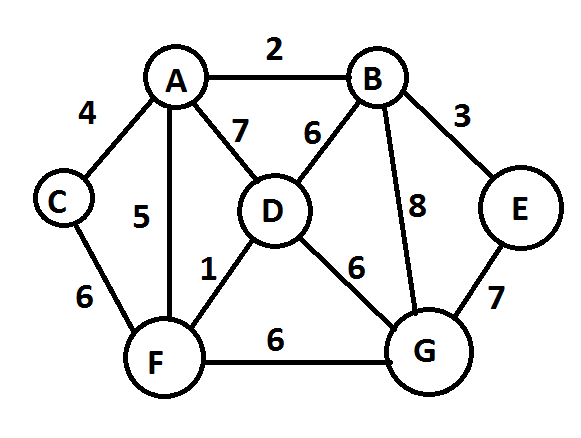
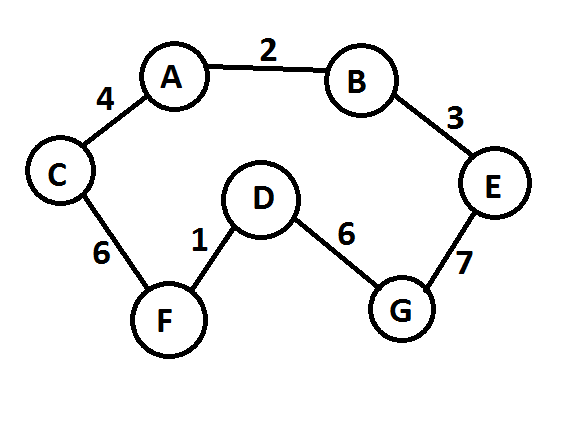
1+2+3+4+2*6++7=29

Найденное решение не обязательно будет самым "дешевым" путем. Гамильтонов цикл.

24. Алгоритмы на графах, решение задачи раскраски графа с помощью жадного алгоритма, принципиальная теоретическая важности задачи раскраски, ее применение

З адача о раскраске графа

(1, 3, 4 - красные, 2,5 - зелёные)

Вершины графа нужно раскрасить в разные цвета. Нас интересуют такие ребра, концы которых окрашены в разные цвета за min кол-во используемых красок (неориентированный граф).

Жадный алгоритм раскраски.

Выбираем произвольную незакрашенную вершину и назначаем ей новый цвет. Рассматриваем список незакрашенных вершин и для каждой из них определяем не соединена ли она с вершиной в новый цвет. Если не соединена, то к ней также применяем новый цвет. Каждый цвет принимается к максимально большому кол-ву вершин. Построение к достаточно близкой к оптимальной раскраске столь не сложно, как и построения оптимальной раскраски.

Число красок, даваемых самым лучшим полиномиальным алгоритмам, более, чем вдвое превышает min-число.

Доказано, что если существует полиномиальный алгоритм, который превышает оптимальное число красок вдвое и существует алгоритм полиномиальной раскраски. У задачи раскраски графов есть приложение — разработка неконфликтного расписания экзаменов.