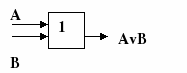Вопрос №1 Перевод из 10-ной системы счисления в 2-ную, 8-ную, 16-ную и обратно.
Для перевода числа из десятичной системы счисления в систему счисления с другим основанием поступают следующим образом:
а) Для перевода целой части числа его делят нацело на основание системы, фиксируя остаток. Если неполное частное не равно нулю продолжают делить его нацело. Если равно нулю остатки записываются в обратном порядке.
б) Для перевода дробной части числа ее умножают на основание системы счисления, фиксируя при этом целые части полученных произведений. Целые части в дальнейшем умножении не участвуют. Умножение производиться до получения 0 в дробной части произведения или до заданной точности вычисления.
в) Ответ записывают в виде сложения переведенной целой и переведенной дробной части числа.
Пример: перевод чисел из десятичной системы счисления в двоичную систему счисления.
Перевести число 75,375 в двоичную систему счисления.
а) переведем в двоичную систему целую часть - 75
75 : 2 = 37 ( 1 )
37 : 2 = 18 ( 1 )
18 : 2 = 9 ( 0 )
9 : 2 = 4 ( 1 )
4 : 2 = 2 ( 0 )
2 : 2 = 1 ( 0 )
1 : 2 = 0 ( 1 )
Закончив деление, запишем остатки в обратном порядке, и получим искомый результат:
75=10010112
б) переведем в двоичную систему дробную часть - 0,375
0,375
2
0,750
2
1,500
2
1,000
Выделенные числа запишем в естественном порядке и получим дробное число в двоичной системе счисления:
0,375 = 0,0112
в) получив целую и дробную части числа в двоичном виде (75=10010112 и 0,375 = 0,0112 ) можем сделать вывод:
75,375=75+0,375 = 10010112+0,0112=1001011,0112, значит 75,375=1001011,0112
Пример: перевод чисел из десятичной системы счисления в шестнадцатеричную систему счисления.
Представить десятичное число 157,23 в шестнадцатеричной системе счисления. Целая часть числа равна 157, дробная - 0,23.
а) переведем в двоичную систему целую часть - 157
157 : 16 = 9 (13 или D)
9 : 16 = 0 ( 9 )
Закончив деление, запишем остатки в обратном порядке, и получим искомый результат:
157=9D 16
а) переведем в двоичную систему дробную часть - 0,23.
Результат умножения 0,23 на 16 равен 3,68. Целая часть этого числа равна 3, значит первый коэффициент дробной части равен 3. Дробная часть равна 0,68. Снова умножим ее на основание системы: 0,68*16=10,88. Целая часть равна 10 или в шестнадцатеричной системе А. Дробная часть равна 0,88, она опять умножается на 16 и так далее.
Выпишем весь процесс:
0,23 * 16 = 3,68 ( 3 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
0,08 * 16 = 1,28 ( 1 )
0,28 * 16 = 4,48 ( 4 )
0,48 * 16 = 7,68 ( 7 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
0,08 * 16 = 1,28 ( 1 )
0,28 * 16 = 4,48 ( 4 )
0,48 * 16 = 7,68 ( 7 )
0,68 * 16 = 10,88 ( А )
0,88 * 16 = 14,08 ( Е )
Замечаем, что последовательность чисел 0,68; 0,88; 0,08; 0,28; 0,48 повторилась уже 2 раза и начинается в третий раз. Получается бесконечная шестнадцатеричная дробь в которой период (бесконечно повторяемая последовательность цифр) заключен в скобки:
157,23=9D,3(АЕ147)16
Для перевода числа в десятичную систему счисления из системы счисления с другим основанием каждый коэффициент переводимого числа умножается на основание системы в степени соответствующей этому коэффициенту и полученные результаты складываются.
Пример: перевод чисел из двоичной системы счисления в десятичную систему счисления
Перевести число 1001011,0112 в десятичную систему счисления
1001011,0112 = 1*26+0*25+0*24+1*23+0*22+1*21+1*20+0*2-1+1*2-2+1*2-3 =64+8+2+1+0,25+0,125=75,375
Двоичная система проста, так как использует две цифры, но громоздка. В десятичной хранить числа в памяти возможно, но сложен перевод из десятичной в двоичную и обратно и занимает много времени. Необходима система счисления компактнее двоичной, но с более простым переводом.
23 = 8 0, 1, 2, 3, 4, 5, 6, 7.
Для перевода из двоичной системы счисления в восьмеричную необходимо разбить данное двоичное число вправо и влево от запятой на триада ( три цифры ) и представить каждую триаду соответствующим восьмеричным кодом. При невозможности разбиения на триады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру восьмеричного числа представляют соответствующей триадой двоичного кода.
Десятичная система счисления |
Двоичная система счисления |
Восьмеричная система счисления |
Шестнадцатеричная система счисления |
|
Триады (0-7) |
Тетрады (0-15) |
|||
0 |
000 |
0000 |
00 |
0 |
1 |
001 |
0001 |
01 |
1 |
2 |
010 |
0010 |
02 |
2 |
3 |
011 |
0011 |
03 |
3 |
4 |
100 |
0100 |
04 |
4 |
5 |
101 |
0101 |
05 |
5 |
6 |
110 |
0110 |
06 |
6 |
7 |
111 |
0111 |
07 |
7 |
8 |
|
1000 |
10 |
8 |
9 |
|
1001 |
11 |
9 |
10 |
|
1010 |
12 |
A |
11 |
|
1011 |
13 |
B |
12 |
|
1100 |
14 |
C |
13 |
|
1101 |
15 |
D |
14 |
|
1110 |
16 |
E |
15 |
|
1111 |
17 |
F |
16 |
10000 |
20 |
10 |
|
Вопрос №2 Перевод из 2-ной системы счисления в 8-ную, 16-ную и обратно.
Пример: перевод чисел из двоичной системы счисления в восьмеричную систему счисления.
Переведем число 1001011,0112 в восьмеричную систему счисления. Разобьем данное число на триады, приписав слева недостающие нули:
001 001 011 , 011
1 1 3 , 3
и заменим каждую триаду соответствующим восьмеричным кодом (см. таблицу). Можем сделать вывод:
1001011,0112 = 113,38
Пример: перевод чисел из восьмеричной системы счисления в двоичную систему счисления.
Переведем число 347,258 в двоичную систему счисления. Каждую цифру восьмеричного числа заменим соответствующей триадой (см. таблицу).
3 4 7 , 2 5
011 100 111 , 010 101
Запишем ответ, удалив нули слева в записи числа:
347,258 = 11100111,0101012
Восьмеричная система компактнее двоичной и с более простым переводом чисел, однако, современные требования к ЭВМ заставили создавать шестнадцатеричную систему счисления.
24 = 16 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Правило перевода из двоичной системы счисления в шестнадцатеричную: разбить двоичное число вправо и влево от запятой на тетрады ( по 4 цифры ) и представить каждую тетраду соответствующим шестнадцатеричным кодом. При невозможности разбиения на тетрады допускается добавление нулей слева в целой записи числа и справа в дробной части числа. Для обратного перевода каждую цифру шестнадцатеричного числа представляют тетрадой двоичного кода.
Пример: перевод чисел из двоичной системы счисления в шестнадцатеричную систему счисления.
Переведем число 1001011,0112 в шестнадцатеричную систему счисления. Разобьем данное число на тетрады, приписав слева в целой части, и справа в дробной части недостающие нули:
0100 1011, 0110
4 В , 6
и заменим каждую тетраду соответствующим шестнадцатеричным кодом (см. таблицу). Можем сделать вывод:
1001011,0112 = 4В,616
Пример: перевод чисел из шестнадцатеричной системы счисления в двоичную систему счисления.
Переведем число А4F,C516 в двоичную систему счисления. Каждую цифру шестнадцатеричного числа заменим соответствующей тетрадой (см. таблицу).
A 4 F , C 5
1010 0100 1111 , 1100 0101
Запишем ответ, удалив нули слева в записи числа:
A4F,C516 = 101001001111,110001012
Вопрос №3 Выполнение арифметических операций в системах счисления.
Арифметические операции в двоичной системе счисления.
Сложение. Таблица двоичного сложения предельно проста. Только в одном случае, когда производится сложение 1+1, происходит перенос в старший разряд.
Пример 1. Рассмотрим несколько примеров сложения двоичных чисел:
1001 1101 11111 1010011,111
+ + + +
1010 1011 1 11001,110
------ ------ --------- --------------
10011 11000 100000 1101101,101
Вычитание. При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и ставится соответствующий знак. В таблице вычитания 1 с чертой означает заем в старшем разряде.
Пример 2. Рассмотрим несколько примеров вычитания двоичных чисел:
10111001,1-10001101,1=101100,0
101011111-110101101= -1001110
10111001,1 110110101
- -
10001101,1 101011111
--------------- --------------
00101100,0 001010110
Умножение. Операция умножения выполняется с использованием таблицы умножения по обычной схеме, применяемой в десятичной системе счисления с последовательным умножением множимого на очередную цифру множителя.
Пример 3. Рассмотрим несколько примеров умножения двоичных чисел:
11001*1101=101000101
11001,01*11,01=1010010,0001
11001 11001,01
* 1101 * 11,01
--------- -----------
11001 1100101
11001 1100101
11001 1100101
------------- -----------------
101000101 1010010,0001
Вы видите, что умножение сводится к сдвигам множимого и сложениям.
Деление. Операция деления выполняется по алгоритму, подобному алгоритму выполнения операции деления в десятичной системе счисления.
Пример 4. Рассмотрим пример деления двоичных чисел:
101000101:1101=11001
101000101 1101
- 1101 11001
1110
-1101
1101
-1101
0
Сложение в других системах счисления. Ниже приведена таблица сложения в восьмеричной системе счисления:
-
+
1
2
3
4
5
6
7
1
2
3
4
5
6
7
10
2
3
4
5
6
7
10
11
3
4
5
6
7
10
11
12
4
5
6
7
10
11
12
13
5
6
7
10
11
12
13
14
6
7
10
11
12
13
14
15
7
10
11
12
13
14
15
16
Вопрос №4 Основные логические операции, порядок их выполнения, таблицы истинности.
Существует 5 основных логических операций:
1) отрицание "не", ā
2) коньюнкция "и", а & b, а^b, a*b
3) дизьюнкция "или", а V b, a I b, a+b
4) импликация "если....то", a→b
5) эквивалентность "а↔b"
Порядок выполнения логических операций в сложном логическом выражении
1.Инверсия; 2.Конъюнкция; 3.Дизъюнкция; 4.Импликация; 5. Эквивалентность.
Для изменения указанного порядка выполнения логических операций используются скобки.
Таблицы истинности:
1)
а |
ā |
0 |
1 |
1 |
0 |
а V b= ā^ƀ
а^b=ā V ƀ
2)
a |
b |
а^b |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
а^b=a
a^ā=0
3)
A |
b |
а V b |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
а V b=a
a V ā =1
4)
a |
b |
a→b |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
5)
a |
b |
a↔b |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
Вопрос №5 Базовые логические элементы и правила их работы.
Условные обозначения:
1)Конъюнктор Схема "и" |
2)Дизъюнктор Схема "или" |
3)Инвертор отрицание |
А
|
|
|
4)
x |
y |
x^y |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
5)
x |
y |
x V y |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
Вопрос №6 История развития вычислительной техники, поколения ЭВМ.
История развития вычислительной техники
Начальный этап развития вычислительной техники
Все началось с идеи научить машину считать или хотя бы складывать многоразрядные целые числа. Еще около 1500 г. великий деятель эпохи Просвещения Леонардо да Винчи разработал эскиз 13-разрядного суммирующего устройства, что явилось первой дошедшей до нас попыткой решить указанную задачу. Первую же действующую суммирующую машину построил в 1642 г. Блез Паскаль - знаменитый французский физик, математик, инженер. Его 8-разрядная машина сохранилась до наших дней.
От замечательного курьеза, каким восприняли современники машину Паскаля, до создания практически полезного и широко используемого агрегата - арифмометра (механического вычислительного устройства, способного выполнять 4 арифметических действия) - прошло почти 250 лет. Уже в начале XIX века уровень развития ряда наук и областей практической деятельности (математики, механики, астрономии, инженерных наук, навигации и др.) был столь высок, что они настоятельнейшим образом требовали выполнения огромного объема вычислений, выходящих за пределы возможностей человека, не вооруженного соответствующей техникой. Над ее созданием и совершенствованием работали как выдающиеся ученые с мировой известностью, так и сотни людей, имена многих из которых до нас не дошли, посвятивших свою жизнь конструированию механических вычислительных устройств. Еще в 70-х годах нашего века на полках магазинов стояли механические арифмометры и их «ближайшие родственники», снабженные электрическим приводом -электромеханические клавишные вычислительные машины. Как это часто бывает, они довольно долго удивительным образом соседствовали с техникой совершенно иного уровня - автоматическими цифровыми вычислительными машинами (АЦВМ), которые в просторечии чаще называют ЭВМ (хотя, строго говоря, эти понятия не совсем совпадают). История АЦВМ восходит еще к первой половине прошлого века и связана с именем замечательного английского математика и инженера Чарльза Бэббиджа. Им в 1822 г. была спроектирована и почти 30 лет строилась и совершенствовалась машина, названная вначале «разностной», а затем, после многочисленных усовершенствований проекта, «аналитической». В «аналитическую» машину были заложены принципы, ставшие фундаментальными для вычислительной техники. 1. Автоматическое выполнение операций. Для выполнения расчетов большого объема существенно не только то, как-быстро выполняется отдельная арифметическая операция, но и то, чтобы между операциями не было «зазоров», требующих непосредственного человеческого вмешательства. Например, большинство современных калькуляторов не удовлетворяют этому требованию, хотя каждое доступное им действие выполняют очень быстро. Необходимо, чтобы операции следовали одна за другой безостановочно. 2. Работа по вводимой «на ходу» программе. Для автоматического выполнения операций программа должна вводиться в исполнительное устройство со скоростью, соизмеримой со скоростью выполнения операций. Бэббидж предложил использовать для предварительной записи программ и ввода их в машину перфокарты, которые к тому времени применялись для управления ткацкими станками. 3. Необходимость специального устройства - памяти - для хранения данных (Бэббидж назвал его «складом»). Эти революционные идеи натолкнулись на невозможность их реализации на основе механической техники, ведь до появления первого электромотора оставалось почти полвека, а первой электронной радиолампы - почти век! Они настолько опередили свое время, что были в значительной мере забыты и переоткрыты в следующем столетии. Впервые автоматически действующие вычислительные устройства появились в середине XX века. Это стало возможным благодаря использованию наряду с механическими конструкциями электромеханических реле. Работы над релейными машинами начались в 30-е годы и продолжались с переменным успехом до тех пор, пока в 1944 г. под руководством Говарда Айкена - американского математика и физика - на фирме IBM (International Business Machines) не была запущена машина «Марк-1», впервые реализовавшая идеи Бэббиджа (хотя разработчики, по-видимому, не были с ними знакомы). Для представления чисел в ней были использованы механические элементы (счетные колеса), для управления - электромеханические. Одна из самых мощных релейных машин РВМ-1 была в начале 50-х годов построена в СССР под руководством Н.И.Бессонова; она выполняла до 20 умножений в секунду с достаточно длинными двоичными числами. Однако, появление релейных машин безнадежно запоздало и они были очень быстро вытеснены электронными, гораздо более производительными и надежными.
НАЧАЛО СОВРЕМЕННОЙ ИСТОРИИ ЭЛЕКТРОННОЙ ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ Подлинная революция в вычислительной технике произошла в связи с применением электронных устройств. Работа над ними началась в конце 30-х годов одновременно в США, Германии, Великобритании и СССР. К этому времени электронные лампы, ставшие технической основой устройств обработки и хранения цифровой информации, уже широчайшим образом применялись в радиотехнических устройствах. Первой действующей ЭВМ стал ENIAC (США, 1945 - 1946 гг.). Его название по первым буквам соответствующих английских слов означает «электронно-числовой интегратор и вычислитель». Руководили ее созданием Джон Моучли и Преспер Эккерт, продолжившие начатую в конце 30-х годов работу Джорджа Атанасова. Машина содержала порядка 18 тысяч электронных ламп, множество электромеханических элементов. Ее энергопотребление равнялось 150 кВт, что вполне достаточно для обеспечения небольшого завода. Практически одновременно велись работы над созданием ЭВМ в Великобритании. С ними связано прежде всего имя Аллана Тьюринга - математика, внесшего также большой вклад в теорию алгоритмов и теорию кодирования. В 1944 г. в Великобритании была запущена машина «Колосс». Эти и ряд других первых ЭВМ не имели важнейшего с точки зрения конструкторов последующих компьютеров качества - программа не хранилась в памяти машины, а набиралась достаточно сложным образом с помощью внешних коммутирующих устройств. Огромный вклад в теорию и практику создания электронной вычислительной техники на начальном этапе ее развития внес один из крупнейших американских математиков Джон фон Нейман. В историю науки навсегда вошли «принципы фон Неймана». Совокупность этих принципов породила классическую (фон-неймановскую) архитектуру ЭВМ. Один из важнейших принципов - принцип хранимой программы - требует, чтобы программа закладывалась в память машины так же, как в нее закладывается исходная информация. Первая ЭВМ с хранимой программой (EDSAC) была построена в Великобритании в 1949 г. В нашей стране вплоть до 70-х годов создание ЭВМ велось почти полностью самостоятельно и независимо от внешнего мира (да и сам этот «мир» был почти полностью зависим от США). Дело в том, что электронная вычислительная техника с самого момента своего первоначального создания рассматривалась как сверхсекретный стратегический продукт, и СССР приходилось разрабатывать и производить ее самостоятельно. Постепенно режим секретности смягчался, но и в конце 80-х годов наша страна могла покупать за рубежом лишь устаревшие модели ЭВМ (а самые современные и мощные компьютеры ведущие производители - США и Япония - и сегодня разрабатывают и производят в режиме секретности). Первая отечественная ЭВМ - МЭСМ («малая электронно-счетная машина») -была создана в 1951 г. под руководством Сергея Александровича Лебедева, крупнейшего советского конструктора вычислительной техники, впоследствии академика, лауреата государственных премий, руководившего созданием многих отечественных ЭВМ. Рекордной среди них и одной из лучших в мире для своею времени была БЭСМ-6 («большая электронно-счетная машина, 6-я модель»), созданная в середине 60-х годов и долгое время бывшая базовой машиной в обороне, космических исследованиях, научно-технических исследованиях в СССР. Кроме машин серии БЭСМ выпускались и ЭВМ других серий - «Минск», «Урал», М-20, «Мир» и другие, созданные под руководством И.С.Брука и М.А.Карцева, Б.И.Рамеева, В.М.Глушкова, Ю.А.Базилевского и других отечественных конструкторов и теоретиков информатики. Поколения электронных вычислительных машин
Первое поколение.
После создания в 1949 г. в Англии модели EDSAC (pict024) был дан мощный импульс развитию универсальных ЭВМ, стимулировавший появление в ряде стран моделей ЭВМ, составивших первое поколение. На протяжении более 40 лет развития ВТ появилось, сменяя друг друга, несколько поколений ЭВМ.
ЭВМ первого поколения в качестве элементной базы использовали электронные лампы и реле; оперативная память выполнялась на триггерах, позднее на ферритовых сердечниках; быстродействие было, как правило, в пределах 5—30 тыс. арифметических оп/с; они отличались невысокой надежностью, требовали систем охлаждения и имели значительные габариты. Процесс программирования требовал значительного искусства, хорошего знания архитектуры ЭВМ и ее программных возможностей. На первых порах данного этапа использовалось программирование в кодах ЭВМ (машинный код), затем появились автокоды и ассемблеры. Как правило, ЭВМ первого поколения использовались для научно-технических расчетов, а сам процесс программирования больше напоминал искусство, которым занимался весьма узкий круг математиков, инженеров-электриков и физиков.