Статистическое изучение динамики общественных явлений

Программа

Ряды динамики как основной источник прогнозирования в экономике. Понятие и классификация рядов динамики. Сопоставимость уровней и смыкание рядов динамики. Показатели динамики, их дифференциация.

Упрощенные приемы прогнозирования. Выявление основной тенденции динамики. Общая характеристика методов прогнозирования.

Прогнозирование на основе рядов динамики.

Одной из важнейших задач статистики является изучение развития процессов и явлений во времени. Это осуществляется с помощью построения и анализа статистических рядов динамики.

Ряд динамики - это последовательность одноименных показателей, расположенных в хронологическом порядке. Ряд динамики характеризуется двумя параметрами: показателем, называемым уровнем ряда у; датой и периодом, к которым относится показатель.

Уровни рядов динамики отображают количественную оценку развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными, или средними величинами.

В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные.

Моментные ряды динамики отображают состояния изучаемых явлений на определенные даты (моменты) времени. Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. Периодом может быть день, неделя, месяц, год.

Для количественной оценки динамики социально-экономических явлений применяются абсолютные и относительные статистические показатели. В основе расчета показателей рядов динамики лежит сравнение его уровней. Если сравнение идет с одним и тем же первым (базисным) уровнем, то вычисляемый показатель называется базисным. Если сравниваются два соседних уровня (каждый последующий уровень ряда сравнивается с предыдущим), вычисляемый показатель называется цепным.

Для выражения изменений уровней рядов динамики в абсолютных величинах вычисляют статистический показатель абсолютного прироста . Величина этого показателя определяется как разность между уровнем изучаемого периода и уровнем, принимаемым за базу сравнения.

При определении базисных абсолютных приростов за базу сравнения принимается постоянный уровень.

.

При определении цепных абсолютных приростов базой сравнения каждый раз выступает уровень предыдущего периода.

.

Абсолютный прирост показывает на сколько единиц текущий уровень больше или меньше предыдущего (базисного).

Между базисными и цепными абсолютными приростами существует связь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего периода ряда динамики.

.

Распространенным статистическим показателем динамики является темп роста (коэффициент роста).

.

Темп роста показывает во сколько раз сравниваемый уровень больше или меньше предыдущего (базисного). Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно последнему базисному темпу роста.

.

Темпы прироста характеризуют абсолютный прирост в относительных величинах. Темп прироста равен отношению абсолютного прироста к уровню ряда, принятому за базу сравнения.

.

Темп прироста показывает на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.

Между темпами роста и прироста имеется взаимосвязь.

.

Значение цепных темпов прироста, рассчитанных каждый к своей базе, различаются не только числом процентов, но и величиной абсолютного изменения, составляющего каждый процент.

Абсолютное значение одного процента прироста выражается отношением абсолютного прироста к темпу прироста. Расчет этого показателя имеет экономический смысл только на цепной основе.

.

Для получения обобщающих показателей динамики социально-экономических явлений применяются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста и другие.

Средний уровень ряда (средняя хронологическая) рассчитывается в зависимости от вида ряда динамики. В интервальном ряду динамики расчет среднего уровня ряда производится по методу средней арифметической простой.

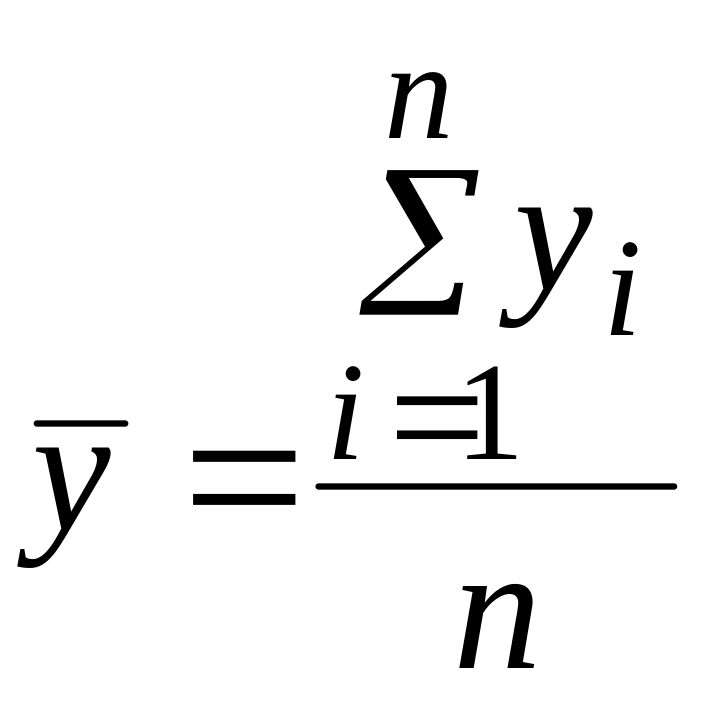, где - уровни ряда; n - число уровней.

В моментном ряду динамики с равноотстоящими датами средний уровень ряда определяется по формуле средней хронологической.

.

В практике экономической работы часто приходится определять средние уровни ряда моментных величин с неравноотстоящими датами времени. Расчет среднего уровня в таких рядах динамики производится по методу средней арифметической взвешенной.

,

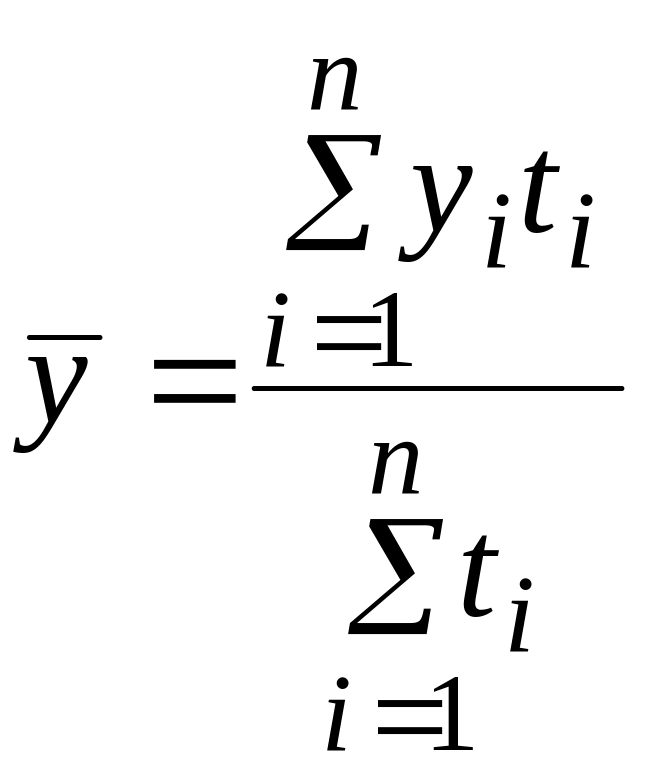где - уровни ряда динамики, сохраняющиеся без изменения в течение промежутков (интервалов) времени .

Средний абсолютный прирост представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.

, .

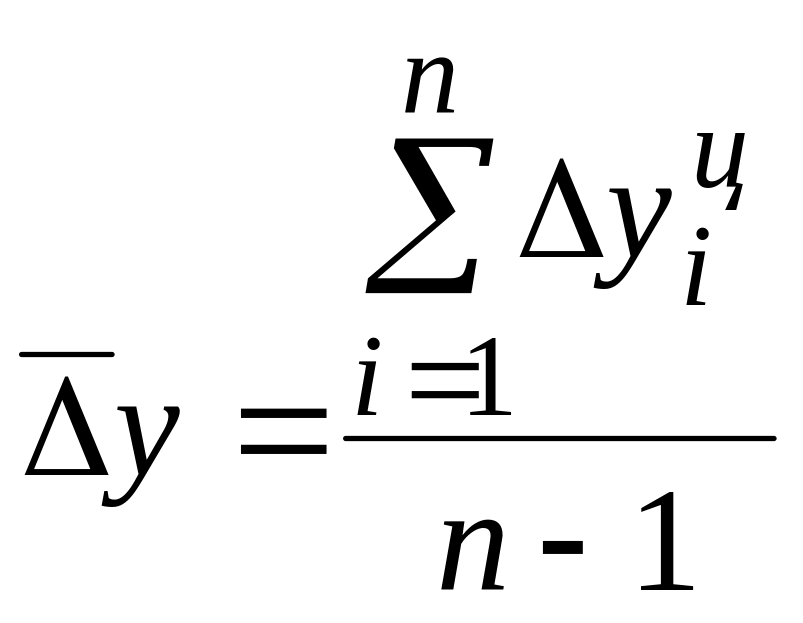Средний темп роста  обобщающая характеристика индивидуальных темпов роста ряда динамики.

,

где n - число уровней ряда; - цепные темпы роста.

На основе взаимосвязи между цепными и базисными темпами роста средний темп роста можно определить по формуле:

.

Средний темп прироста можно определить на основе взаимосвязи между темпами роста и прироста.

.

Абсолютным ускорением называется разность между двумя абсолютными приростами.

.

Относительным ускорением называется отношение абсолютного ускорения к абсолютному приросту, принятому за базу.

.

Пример 1. Ряд динамики розничного товарооборота магазина характеризуется следующими данными:

Период	I	II	III	IV	V
Объем товарооборота, тыс. руб.	885.7	932.6	980.1	1028.7	1088.4

Необходимо рассчитать абсолютные и относительные показатели ряда динамики. Представим расчеты в виде таблицы.

Период	Товарооборот, тыс.руб.	Абсолютный прирост, тыс. руб.		Темп роста, %		Темп прироста, %		Темп наращивания
		Б	Ц	Б	Ц	Б	Ц
I	885.7							
II	932.6	46.9	46.9	105.3	105.3	5.3	5.3	5.3
III	980.1	94.4	47.5	110.6	105.1	10.6	5.1	5.4
IV	1028.7	143.0	48.6	116.1	104.9	16.1	4.9	5.5
V	1088.4	202.7	59.7	122.9	105.8	22.9	5.8	6.8

Из таблицы видно, что по сравнению с первым периодом в каждом последующем периоде происходило систематическое увеличение абсолютных приростов товарооборота (тыс.руб.): 46.9<94.4<143.0<202.7.

Цепные абсолютные приросты показывают, что нарастание объемов товарооборота происходило из периода в период: 46.9<47.5<48.6<59.7.

Абсолютный прирост может иметь и отрицательный знак, показывающий на сколько уровень текущего периода ниже базисного. По цепным абсолютным приростам определяется базисный абсолютный прирост:

= 46.9+47.5+48.6+59.7 = 202.7 тыс. руб.

В V периоде по сравнению с I периодом товарооборот увеличился на 202.7 тыс.руб. Базисные темпы роста показывают, что по сравнению с I периодом происходило систематическое увеличение товарооборота магазина, достигшего в V периоде 122.9% базисного уровня. Цепные темпы роста показывают, что в развитии товарооборота имело место замедление темпов (%): 105.3>105.1>104.9<105.8. Проверим связь цепных и базисных темпов роста: 1.0531.0511.0491058 = 1.229.

Средний уровень ряда: =(885.7+...+1088.4):5=983.1 тыс.руб. С I периода по V период товарооборот в среднем составлял 983.1 тыс. руб. Средний абсолютный прирост: =(46.9+47.5+48.6+59.7):4=50.7 тыс. руб. ( =(1088.4885.7):4=50.7 тыс. руб.). С I периода по V период ежегодно объем товарооборота возрастал в среднем на 50.7 тыс. руб. Средний темп роста: . С I периода по V период товарооборот ежегодно возрастал в среднем в 1.053 раза или на 5.3 %.

Важной задачей статистики при анализе рядов динамики является определение общей тенденции развития. На развитие явления во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них оказывают более или менее постоянное воздействие и формируют в рядах динамики определенную тенденцию развития (тренд). Воздействие же других факторов может быть кратковременным.

При изучении колеблемости цен в динамике определяется тенденция их изменения во времени. Тренд, вокруг которого варьируют цены, рассматривается как общая закономерность динамики цен. Основные способы статистического выявления тренда заключается в укрупнении интервалов, сглаживании ряда с помощью скользящей средней и аналитическом выравнивании.

В общем виде трендовая модель для отдельной цены или индекса цен может быть выражена как функция , где t - номер периода. Модель отражает не только направление изменения, но и его характер (ускорение, замедление), а также дает количественную оценку среднего изменения за период, которая определяется как первая производная соответствующей функции.

Метод укрупнения интервалов применяется для выявления тренда в рядах динамики колеблющихся уровней, затушевывающих основную тенденцию развития. Этот метод основан на укрупнении периодов, к которым относятся уровни ряда динамики.

Пример 2. Имеются данные о реализации товаров в одном из магазинов города.

Январь	23.2	июль	28.4
февраль	19.1	август	24.1
Март	22.3	сентябрь	26.3
Апрель	25.1	октябрь	29.1
Май	24.5	ноябрь	30.3
Июнь	27.3	декабрь	26.5

Различные направления изменений по отдельным месяцам уровней данного ряда динамики затрудняют выводы об основной тенденции продажи товаров. Для выявления общей тенденции реализации товаров произведем укрупнение интервалов. Для этой цели исходные (месячные) данные о реализации товаров преобразуем в квартальные.

1 кв.	2 кв.	3 кв.	4 кв.
64.5	76.9	78.8	85.9

В результате укрупнения интервалов общая тенденция роста продажи товаров становится очевидной. 64.5 < 76.9 < 78.8 < 85.9 .

Для статистического изучения тренда применяется так называемое сглаживание методом скользящей средней. Сущность метода состоит в том, что по исходным уровням ряда (эмпирическим данным) определяют расчетные (теоретические) уровни, в которых случайные тенденции погашаются, а основная тенденция развития выражается в виде некоторой плавной линии.

Применение этого метода рассмотрим на данных о реализации продуктов.

Квартал	1 год	2 год	3 год	4 год
1	175	247	420	426
2	263	298	441	449
3	326	366	453	482
4	297	341	399	460

Для выражения общей тенденции развития явления методом сглаживания рядов динамики необходимо, прежде всего определить по исходным данным подвижные (скользящие) средние. Основное условие применения этого метода состоит в вычислении звеньев скользящей средней.

Для ряда внутригодовой динамики с сезонными циклами развития явления по кварталам применяют четырехчленные скользящие средние. Их расчет состоит в определении средних величин из 4-х уровней ряда с отбрасыванием при вычислении каждой новой скользящей средней одного уровня слева и присоединением одного уровня справа:

; .

Расчет скользящих средних представим в таблице.

Период	Исходные уровни у	Скользящие средние у0	Сглаженные уровни уi
1 год 1 кв.	175
2 кв.	263	1061:4=265.25
3 кв.	326	1133:4=283.25	(265.25+283.25):2=274.25
4 кв.	297	1168:4=292.00	(283.25+292.00):2=287.6
2 год 1 кв.	247	1208:4=302.00	297.0
2 кв.	298	1252:4=313.00	307.5
3 кв.	366	1425:4=356.25	334.6
4 кв.	341	1568:4=392.00	374.1
3 год 1 кв.	420	1655:4=413.75	402.9
2 кв.	441	1713:4=428.25	421.0
3 кв.	453	1719:4=429.25	429.0
4 кв.	399		430.75
4 год 1 кв.	426	1727:4=431.75	435.37
2 кв.	449	1756:4=439.00	446.62
3 кв.	482	1817:4=454.25
4 кв.	460

Для определения сглаженных уровней производится центрирование. Если при сглаживании рядов динамики звенья скользящей средней составляются из нечетного числа уровней, то необходимость в центрировании отпадает. Применение в анализе рядов динамики методов укрупнения интервалов и скользящей средней позволяет выявить тренд для его описания, но получить обобщенную статистическую оценку тренда с помощью этих методов невозможно.

Изменение тренда достигается с помощью метода аналитического выравнивания. Основным содержанием метода аналитического выравнивания в рядах динамики является то, что основная тенденция развития рассчитывается как функция времени . Определение теоретических уровней производится на основе так называемой адекватной математической функции, которая наилучшим образом отображает основную тенденцию развития ряда динамики. Допустим, что функция имеет вид прямолинейного тренда: . Для нахождения и составляем систему уравнений

Если тенденция явления имеет вид параболы , то для нахождения , и составляем систему уравнений

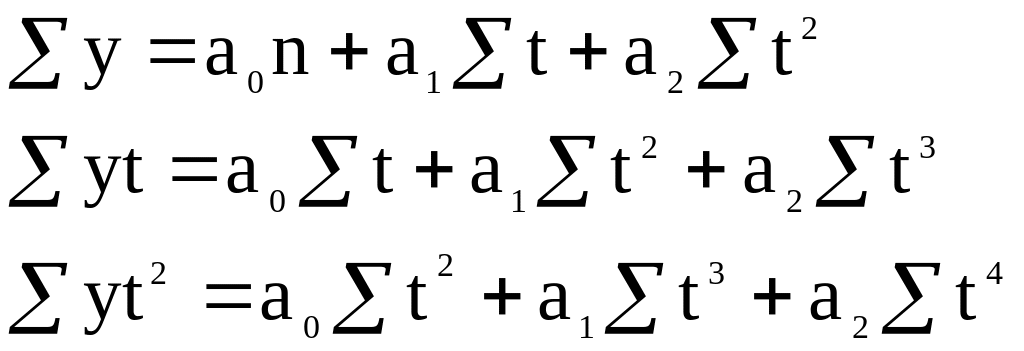
Пример 3. Имеются данные о выпуске продукции предприятиями легкой промышленности за ряд периодов в сопоставимых ценах, млн. руб.

I	II	III	IV	V	VI	VII	VIII	IX
221	235	272	285	304	320	360	371	395

Иногда для простоты расчетов можно решить систему уравнений, приняв =0. Для расчета составим рабочую таблицу:

Период	Эмпирические значения	Условные обозначения времени t	t	yt	yt
I	221	4	16	884	219.32
II	235	3	9	705	241.24
III	272	2	4	544	263.16
IV	285	1	1	285	285.08
V	304	0	0	0	307.0
VI	320	1	1	320	328.92
VII	360	2	4	720	350.84
VIII	371	3	9	1113	372.76
IX	395	4	16	1580	394.68
Итого	2763	0	60	1315	2763

Вычислим значения: ; . Подставив , в исходное линейное уравнение, получим: .

Важное место в анализе рядов динамики занимает изучение сезонных колебаний с помощью индексов сезонности. По данным одного года индексы сезонности рассчитываются как процентное отношение помесячных уровней к среднему уровню за год, т.е. . Для большей надежности сезонность изучается по данным за три года. В этом случае для каждого месяца рассчитывается средний уровень за три года, который и сопоставляется со средним уровнем за весь период .

Чтобы учесть и имеющую место тенденцию изменения, рекомендуется производить сглаживание ряда способом скользящей средней или по аналитическим формулам, а затем находить отношение фактического уровня каждого месяца к выровненному, т.е.

.

Для учета сезонной волны при прогнозировании из полученных отношений для одноименных месяцев (кварталов) рассчитывается средняя величина.

Квартал			Средние индексы сезонности
2001-1 2 3 4 2002-1 2 3 4	298.8 228.9 118.4 270.4 307.3 301.5 152.7 286.2	121.7 93.2 48.2 110.1 125.2 122.8 62.2 116.5	123.45 108.00 55.20 113.30 123.45 108.00 55.20 113.30
Всего	1964.2	-

1. Рассчитываем средний квартальный уровень за два года. .

2. Рассчитываем индексы сезонности (гр.3).

3. По данным двух лет рассчитываем средний индекс для каждого квартала.

Поскольку в квартальных уровнях имеется тенденция к снижению, то рекомендуется произвести аналитическое выравнивание ряда, а затем индексы сезонности рассчитать как отношение к выровненным уровням, а не к общей средней. Для выравнивания примем линейную функцию. Если тренд в виде прямой, то . Для нахождения и составляем систему уравнений, а затем рабочую таблицу.

Квартал						Средние индексы сезонности	Выровненные уровни с учетом сезонности
1	2	3	4	5	6	7	8=гр.5*гр.7
1 2 3 4 1 2 3 4	298.8 228.9 118.4 270.4 307.3 301.5 152.7 286.2	1 4 9 16 25 36 49 64	298.8 457.8 355.2 1081.6 1536.5 1809.0 1068.9 2289.6	240.62 242.02 243.42 244.82 246.22 247.62 249.02 250.42	124.2 94.6 48.6 110.4 124.8 121.8 61.3 114.3	124.5 108.2 55.0 112.4 124.5 108.2 55.0 112.4	299.6 261.9 133.9 275.2 306.5 267.9 137.0 281.5
36	1964.2	204	8897.4	1964.2	-	-	1963.5

Уравнение тренда примет вид

Лекция 8, 9. Одной из важнейших задач статистики является изучение развития процессов и явлений во времени. Это осуществляется с помощью построения и анализа статистических рядов динамики. На развитие явления во времени могут оказывать влияние различные по своему характеру и силе воздействия факторы. Одни из них оказывают более или менее постоянное воздействие и формируют в рядах динамики определенную тенденцию развития (тренд). Воздействие же других факторов может быть кратковременным. Основные способы статистического выявления тренда заключается в укрупнении интервалов, сглаживании ряда с помощью скользящей средней и аналитическом выравнивании. Важной проблемой является подбор математической функции, по которой рассчитываются теоретические уровни тренда. От правильности решения этой проблемы зависят выводы о закономерностях тренда изучаемых явлений.

При изучении данной темы необходимо обратить особое внимание на расчет показателей динамики, их дифференциацию на абсолютные и относительные, цепные и базисные.; на выявление основной тенденции и экстраполяции на основе рядов динамики.

Практическое занятие 6. Решение задач по теме.

Задание 1. Имеются данные о производстве кожаной обуви в республике Беларусь:

Объем производства, млн пар	45,3	37,2	33,4	26,4	16,5	13,0	11,4	11,2	13,2
Периоды	1998	1999	2000	2001	2002	2003	2004	2005	2006

Определить:

- аналитические показатели абсолютного прироста, темпа роста, темпа прироста;

- средний абсолютный прирост, средний темп роста, средний темп прироста;

- составить уравнение тренда, определить прогноз на 2009 год.

Задание 2. Существуют данные о грузообороте транспорта в Российской Федерации (тыс. т).

Месяцы	2002	2003	2004
Январь	283	277.8	276.7
Февраль	266.8	250.5	250.9
Март	288.5	282.3	289.6
Апрель	273	264.8	275.5
Май	267.4	257.5	280.6
Июнь	255.8	254.5	268.8
Июль	260.1	256.9	273.1
Август	256.9	256.9	278.2
Сентябрь	261.2	245.9	271.7
Октябрь	274.4	274.2	289.6
Ноябрь	279.1	269.6	286.1
Декабрь	289.4	279.5	303.8

Для изучения общей тенденции грузооборота транспорта в РФ:

1. Рассчитать показатели динамики по годам и сделать вывод.

2. Провести преобразование исходных данных путем укрупнения периодов времени в квартальные уровни. Нанести на график полученные квартальные уровни.

3. Произвести сглаживание квартальных уровней методом скользящей средней. Нанести полученные при сглаживании данные на график с квартальными уровнями.

4. Составить уравнение линейного тренда. Составить прогноз на 2006 год.

Задание 3. Ежедневное поступление за март в областной бюджет по всем видам налогов (тыс. руб.) представлено в таблице.

01.03	02.03	05.03	06.03	07.03	11.03	12.03	13.03	14.03	15.03	16.03
8	9	12	10	9	5	7	10	16	4	13

19.03	20.03	21.03	22.03	23.03	26.03	27.03	28.03	29.03	30.03
12	9	8	5	11	14	9	7	15	6

На основании приведенных данных проведите исследование ряда динамики.

Задание 4. В виде таблицы приведены данные о потреблении продуктов питания на территории РФ (в среднем на душу населения).

Продукты питания	1998	1999	2000	2001	2002	2003	2004
Хлеб	124	125	121	117	118	118	119
Картофель	127	123	124	125	130	123	123
Овощи	71	69	76	75	79	78	79
Молоко	294	278	253	233	230	221	205
Яйца (шт.)	250	236	214	207	210	218	227
Сахар	31	31	32	33	33	33	34
Мясо	59	57	55	51	50	48	42

Выполнить анализ ряда динамики.

Задание 5. Ниже приведены данные о доходах парка аттракционов в городе (тыс. руб.).

Месяцы	Аттракционы
	2001	2002	2003
Январь	5.2	8.3	13
Февраль	7	5	17.5
Март	11.5	14.4	14.7
Апрель	88.9	90	50
Май	105	100.5	120
Июнь	200	300	400.9
Июль	280	370	500
Август	290	290	570.4
Сентябрь	210	200.5	220
Октябрь	105.7	100	99.7
Ноябрь	14	15.9	20.4
Декабрь	9.3	7	6

Произведите анализ сезонных колебаний и постройте график сезонной волны по каждому году.

Задание 6. Численность населения двух городов составляла (тыс. чел.):

	город А	город В
на 1 января 2006 г.	75.0	151.1
на 1 апреля	75.1	151.3
на 1 июля	75.2	151.2
на 1 октября	75.5	152.0
на 1 января 2007 г.	75.8	152.1

Определить среднюю численность населения за каждое полугодие 2006 года и за год в целом. Рассчитать темпы роста численности населения городов. Выполнить анализ.

Лабораторная работа 3. Комплексный анализ ряда динамики, прогноз развития конкретного социально – экономического явления.

Самостоятельная работа: написание эссе, составление алгоритма.

Подробное изложение материала по теме представлено в основной литературе обязательная - [2,7,10], 7 – стр.142 – 168, - дополнительная - [8, 9].

Для закрепления теории необходимо ответить на основные вопросы:

1. В чем состоит значение рядов динамики (РД). Какие принципы составления РД вы знаете.

2. Как дифференцируются ряды динамики.

3. Какие показатели применяются для характеристики ряда динамики.

4. Какие виды средних используются для расчета среднего уровня рядов динамики.

3. Что такое цепная и базисная основа расчета показателей динамики?

4. Перечислите аналитические показатели РД.

5. Какие свойства показателей РД вы знаете.

6. Какие вы знаете методы выявления и анализа основной тенденции ряда динамики.

7. Какова роль аналитического выравнивания уровней ряда динамики.

8. Как выполнить прогноз на будущее с помощью уравнения тренда.

9. Какие методы могут быть использованы для выявления сезонных колебаний.

Задания для текущего тестирования

1. Ряд динамики характеризует:

а. изменение значений признака во времени

б. значение признака на определенную дату или за определенный период

в. структуру совокупности по какому- либо признаку

г. определенное значение варьирующего признака в совокупности

2. Параметрами ряда динамики являются:

а) размах вариации; б) уровень ряда; в) дата (период);

г) среднее квадратическое отклонение.

3. Абсолютный прирост вычисляется как:

а) отношение уровней ряда; б) разность уровней ряда.

Темп роста вычисляется как:

а) отношение уровней ряда; б) разность уровней ряда.

4. Средний уровень моментного ряда при неравных интервалах между датами исчисляется как средняя…

а. арифметическая простая, б. геометрическая,

в. арифметическая взвешенная, г. хронологическая взвешенная,

д. хронологическая простая

5. Средний уровень ряда в интервальных рядах динамики с неравными интервалами исчисляется по формуле:

а. средней хронологической б. средней арифметической взвешенной

в. средней геометрической г. средней арифметической

6. Абсолютными показателями ряда динамики являются:

а) абсолютный прирост; б). темп роста;

в). средний уровень ряда; г). темп прироста.

7. К относительным показателям ряда динамики относятся:

а) абсолютный прирост;

б). темп роста;

в). средний абсолютный прирост;

г). темп прироста.

8. Какой показатель динамики показывает: «на сколько процентов сравниваемый уровень больше или меньше предыдущего (базисного).

а). абсолютный прирост;

б). темп роста;

в). темп прироста.

9. Какому показателю ряда динамики присуще свойство: «произведение последовательных цепных показателей равно последнему базисному показателю»:

а). абсолютный прирост;

б). темп роста;

в). темп прироста.

10. Какие методы из указанных ниже наиболее часто используются на практике для отслеживания в рядах динамики тенденции развития (тренда)?

а) метод укрупнения интервалов;

б) метод скользящей средней;

в) метод аналитического выравнивания.

11. Для прогнозирования тенденции развития социально-экономических явлений используются методы статистического исследования:

а). ряды распределения; б). ряды динамики;

в). корреляционные взаимосвязи; г). экономические индексы.

12. Среднегодовой коэффициент роста (снижения)в рядах динамики исчисляется по формуле средней:

а. кубической, б. геометрической, в. арифметической, г. гармонической

13. Средний темп роста применяется:

а. для приведения данных к сопоставимому виду

б. для оценки сезонных колебаний

в. для оценки тесноты связи

г. для краткосрочного прогнозирования

14. Укажите показатель изменения уровней ряда динамики, который может принимать отрицательные значения:

а. абсолютный прирост б. темп роста в. темп прироста

г. средний темп прироста д. средний темп роста

15. Величину абсолютного изменения признака в текущем периоде по сравнению с базисным характеризует базисный:

а. темп прироста б. коэффициент роста в. абсолютный прирост

г. темп роста

16. Величина абсолютного изменения признака за определенный промежуток времени характеризуется:

а. цепным абсолютным приростом

б. ценным темпом прироста

в. базисным коэффициентом роста

г. базисным абсолютным приростом

д. цепным темпом роста

17. Имеются остатки оборотных средств на начало каждого месяца: 1.01 – 200, 1.02. – 220, 1.03 – 180, 1.04 – 260. Средние остатки оборотных средств за квартал:

а. 60; б. 200; в. 215; г. 210

18. Если за два периода темп роста объемов производства составил 140%, то это значит, что объем производства увеличился:

а. в 4 раза; б. на 140%; в. на 40%; г. в 14 раз

19. Анализ сезонных колебаний позволяет выявить:

а. прогноз погоды

б. закономерно повторяющиеся различия в уровне рядов динамики в зависимости от времени года

в. изменения в распределении единиц изучаемого явления по субъектам РФ в динамике

г. тенденции развития явления в динамике

20. Для получения базисного коэффициента роста в текущем периоде необходимо:

а. суммировать все цепные коэффициенты роста

б. разделить уровень текущего периода на уровень базисного периода

в. перемножить все цепные коэффициенты роста

г. разделить уровень текущего периода на уровень предыдущего периода

21. Основание или база сравнения – это:

а. сравниваемая величина б. величина, с которой сравнивают

в. генеральная совокупность г. часть изучаемой совокупности

22. Сезонные колебания в ряду могут быть описаны с помощью …

а. факторов сезонности б. параметров сезонности в. индексов сезонности

г. коэффициентов сезонности

23. Расчет среднегодового темпа роста уровня среднедушевого денежного дохода производится в форме средней … , если известно, что в 2004 г., по сравнению с 2000 г., он увеличился на 14,5 %

а. арифметической взвешенной

б. гармонической взвешенной

в. арифметической простой

г. гармонической простой

д. геометрической

24. Средний абсолютный прирост является параметром

а. показательной модели тенденции

б. степной модели тенденции

в. линейной модели тенденции

г. квадратичной модели тенденции

25. Интерполяция – это:

а. диагностика

б. интервальная оценка прогноза

в. метод прогнозирования размеров явлений в будущем

г. прогнозирование неизвестных уровней ряда динамики в прошлом

26. При исследовании развития процессов в динамике признак времени регистрации фактов измеряется:

а. в номинальной шкале;

б. в порядковой шкале;

в. в шкале разностей;

г. все ответы в различных случаях могут быть верными.

27. Наращение по правилу простого процента происходит по сравнению с наращением по правилу сложного процента…

а. быстрее в рамках одного года, затем медленнее

б. быстрее

в. одинаково

г. медленнее в рамках одного года, затем быстрее

д. медленнее

28. Быстрый абсолютный прирост равен:

а. корню n-степени из суммы абсолютных приростов

б. произведению цепных абсолютных приростов

в. корню n-степени из произведения цепных абсолютных приростов

г. сумме цепных абсолютных приростов

29. Прогнозирование основано

а. на инертности социально-экономических явлений

б. на оценке влияния внутренних факторов

в. на оценке влияния внешних факторов

г. на устойчивости статистических показателей

30. Наиболее точный метод прогнозирования – это

а. прогнозирование на основе индексного метода

б. прогнозирование по среднему абсолютному приросту

в. экстраполяция на основе трендовой модели

г. прогнозирование по среднему темпу роста

Статистические методы изучения взаимосвязей

Программа

Взаимосвязи явлений и необходимость их статистического изучения. Виды и формы взаимосвязей. Простейшие статистические методы изучения взаимосвязей. Уравнение регрессии как форма аналитического выражения статистической связи. Выбор формы связи.

Показатели оценки тесноты взаимосвязи. Использование корреляционно – регрессионного анализа в социально – экономических исследованиях. Применение методов динамики и корреляционно - регрессионного анализа для исследования экономической конъюнктуры рынка.

Во многих экономических исследованиях требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других случайных величин. Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической зависимостью, либо быть независимыми.

Строгая функциональная зависимость реализуется очень редко, т.к. обе величины или одна из них подвержены действию случайных факторов. В этом случае возникает статистическая зависимость.

Статистической называется зависимость, при которой изменение одной из величин влечет за собой изменение распределения другой. В частности статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой, в этом случае статистическая зависимость называется корреляционной.

При наличии функциональной зависимости между признаками можно, зная величину факторного признака, точно определить величину результативного признака. При наличии корреляционной зависимости устанавливается лишь тенденция изменения результативного признака при изменении величины факторного признака.

С помощью статистических методов изучения зависимостей можно установить, как проявляется теоретически возможная связь в данных конкретных условиях. Статистика не только отвечает на вопрос о реальном существовании намеченной теоретическим анализом связи, но и дает количественную характеристику этой зависимости.

При статистическом анализе различают корреляцию (существует ли взаимосвязь между X и Y ? Как сильна она?) и регрессию (какая зависимость между X и Y ? Можно ли ее оценить?).

Корреляционной зависимостью Y от X называется функциональная зависимость условной средней от x. . Это уравнение регрессии Y на X Функцию f(x) называют регрессией Y на X , а ее график – линией регрессии Y на X. Аналогично определяется корреляционная зависимость X на Y.

Корреляционный анализ включает в себя:

- предварительный анализ свойств моделируемой совокупности единиц;

- установление факта наличия связи; определение ее направления и формы;

- оценку тесноты корреляционной связи;

- построение регрессионной модели, т.е. нахождение аналитического выражения связи;

- оценку адекватности модели, ее экономическую интерпретацию и практическое использование;

Основными задачами при изучении корреляционной зависимости являются: отыскание математической модели (формы связи), которая выражает эту зависимость и измерение тесноты этой зависимости (связи). Определение формы связи называется нахождением уравнения связи (уравнения регрессии). Возможны различные формы связи:

- линейная - ;

- нелинейная (парабола - ; гипербола - ; показательная функция - ).

Параметры для уравнений связи находятся из системы нормальных уравнений.

Для прямой

Для параболы

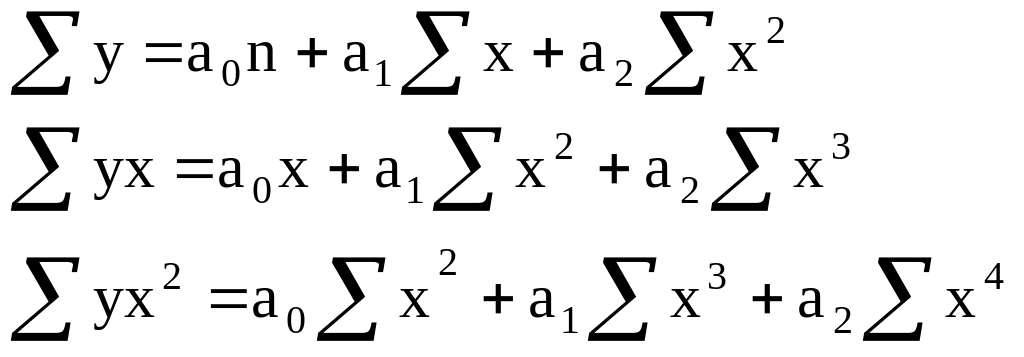
Вторая задача – измерение тесноты - связи может быть решена с помощью расчета теоретического корреляционного отношения , где дисперсия в ряду выравненных значений результативного показателя; - дисперсия в ряду фактических значений у.

Так как дисперсия отражает вариацию в ряду только за счет вариации фактора х, а дисперсия отражает вариацию у за счет всех факторов, то их отношение показывает, какой удельный вес в общей дисперсии ряда у занимает дисперсия, вызываемая вариацией фактора х.

Линейный коэффициент корреляции можно определить по формуле ,

где - средняя арифметическая простая произведений факторных и результативных признаков,

- средняя арифметическая простая факторных признаков,

- средняя арифметическая простая результативных признаков,

- среднее квадратическое отклонение факторных признаков,

- среднее квадратическое отклонение результативных признаков.

Линейный коэффициент корреляции может принимать значения от -1 до +1. –1   +1

Пример 1. Провести анализ взаимосвязи между ценой и спросом на товар А.

Период	Объем продаж, тыс. ед.	Цена, руб. за ед.
1 2 3 4 5	510 480 270 210 90	12 16 38 39 55

Модель зависимости спроса от уровня цен представим в виде динамической регрессионной модели. . Для построения модели по прямолинейному уравнению регрессии составляем систему нормальных уравнений:

Для нахождения коэффициентов системы составляем таблицу.

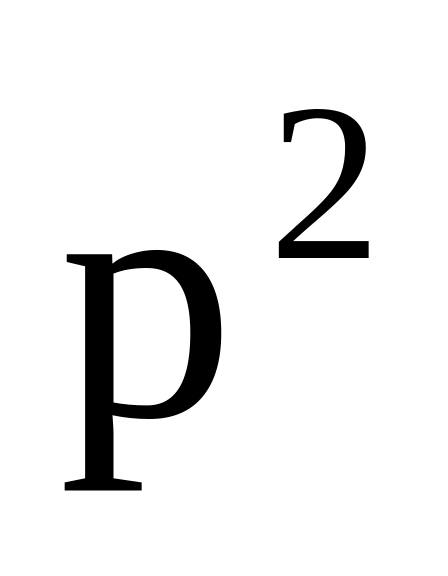
Период	Q	p		pq
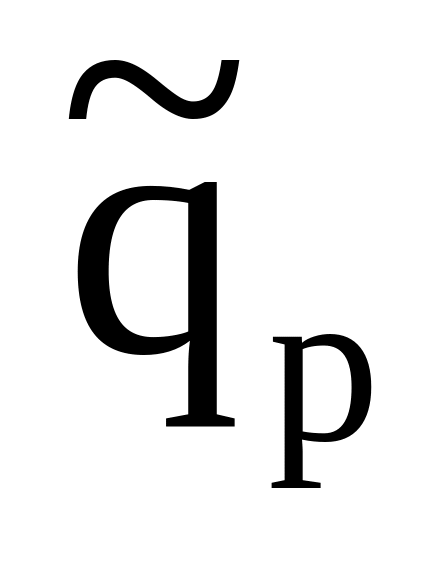
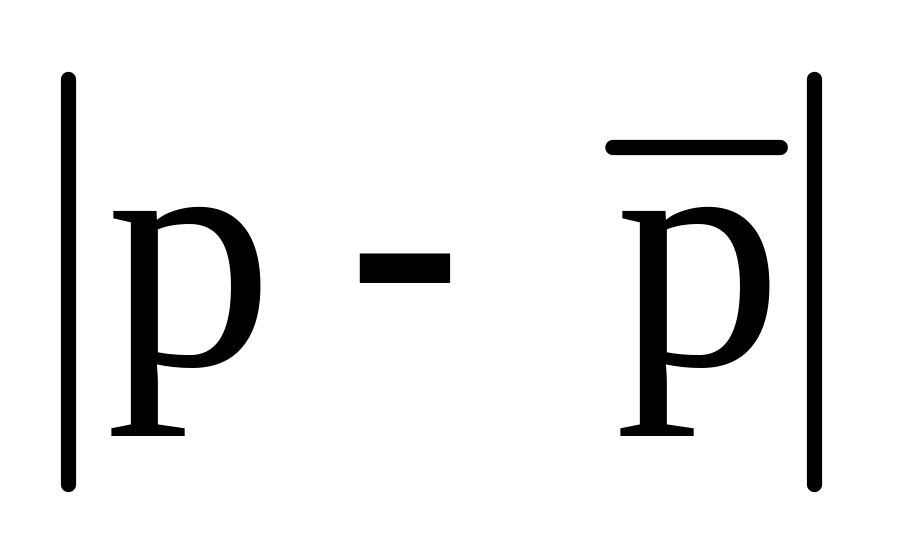
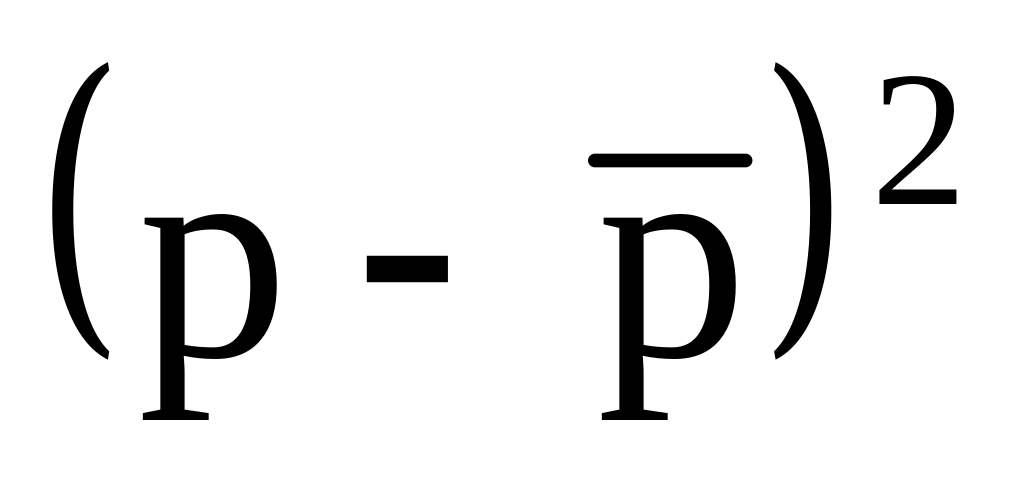
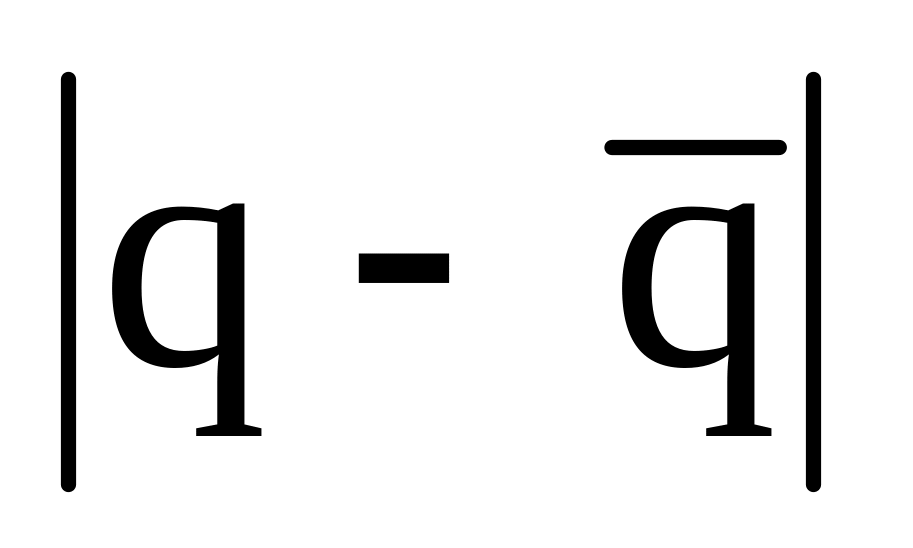
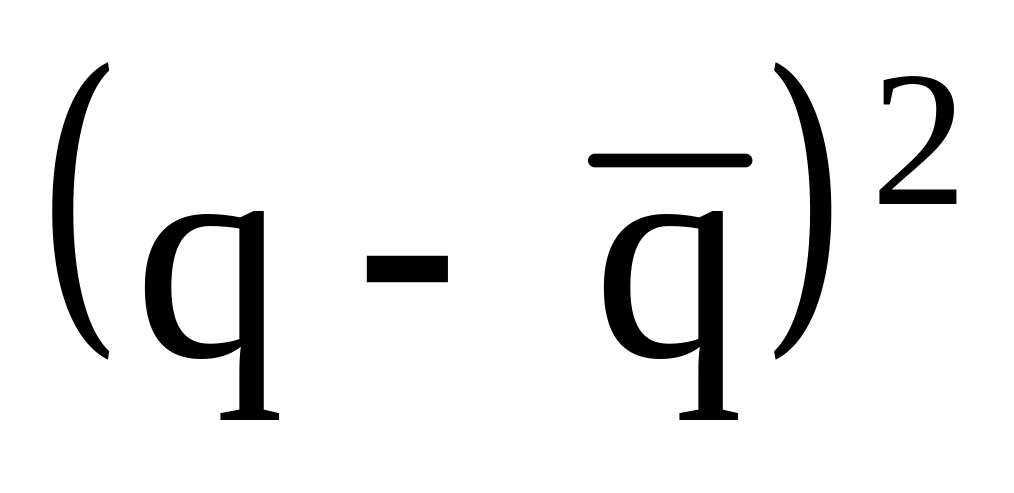
1 2 3 4 5	510 480 270 210 90	12 16 38 39 55	144 256 1444 1521 3025	6120 7680 10260 8190 4950	512 472 252 242 82	20 16 6 7 23	400 256 36 49 529	198 168 42 102 222	39204 28224 1764 10404 49284
Всего	1560	160	6390	37200	1560		1270		128880

Подставляя данные в систему уравнений, получаем уравнение регрессии , т.е. при исключении всех прочих факторов, при увеличении цены на 1 тыс. руб. , спрос на товар А падал в среднем на 10 тыс. ед.

Теснота связи определяется по коэффициенту линейной корреляции

Связь тесная и обратная.

Примечание: ; ; ;

Лекция 10. Исследование объективно существующих связей между явлениями – важнейшая задача статистики. Социально-экономические явления представляют собой результат воздействия большого числа факторов. При изучении этих явлений необходимо выявлять главные, абстрагируясь от второстепенных. Поэтому в данной теме особое внимание следует уделять экономической интерпретации явлений.

Первый этап статистического изучения взаимосвязей - качественный анализ явления; второй - построение модели связи; третий этап – интерпретация результатов. Основными вопросами при изучении темы являются установление вида зависимости между явлениями: функциональная или статистическая; отыскание математической модели (формы связи), которая выражает эту зависимость и измерение тесноты зависимости (связи), экономическая интерпретация полученных результатов.

Практическое занятие 7. Практические занятия по данной теме предусматривают решение задач по регрессионному и корреляционному анализу: расчет параметров уравнения прямой и параболы; расчет коэффициента корреляции.

Задание 1. Имеются следующие данные по 10 однородным предприятиям.

№ предприятия	1	2	3	4	5	6	7	8	9	10
Энерговооруженность труда на одного работника, кВт  ч	2	5	3	7	2	6	4	9	8	4
Выпуск готовой продукции на одного работника, млн руб.	3	6	4	6	4	8	6	9	9	5

Найти уравнение прямой регрессии – зависимость между энерговооруженностью труда и продукцией на одного работника.

Задание 2. По семи однородным семьям имеются следующие данные о доходах и потреблении молока за месяц (на одного члена семьи):

№ семьи	1	2	3	4	5	6	7
Доход, тыс. руб.	540	630	740	900	112	140	190
Потребление молока, л	8	10	11	13	15	17	19

Найдите уравнение корреляционной связи между доходом и потреблением молока. Проанализируйте параметры уравнения регрессии. Изобразите графически данную зависимость.

Задание 3. Для работы в компании "Сотел - НН" среди отобранных кандидатов проводились тесты. Результаты тестов с точки зрения знания экономики и компьютерного анализа данных представлены в таблице.

	К 1	К 2	К 3	К 4	К 5	К 6	К 7	К 8	К 9	К 10
Экономика	12	14	15	15	18	19	20	23	23	25
Анализ данных	16	19	21	15	22	17	23	21	25	26

Определить существует ли зависимость между баллами, полученными по экономике и компьютерному анализу данных. Определить коэффициент корреляции.

Задание 4. Найти выборочное уравнение прямой регрессии Y на Х.

№ магазина	1	2	3	4	5	6	7	8	9	10
Площадь торгового зала м2	85	108	74	65	52	84	120	103	89	80
Товарооборот, млн. руб.	65	72	62	61	55	62	74	68	68	64

Задание 5. Отдел маркетинга компании "Джонсон и Джонсон" провел анализ месячных расходов на рекламу и объема продаж выпускаемой продукции. Полученные данные представлены в таблице.

Месяц	Я	Ф	М	А	М	И	И	А	С	О	Н	Д
Выручка, млн. руб.	3,0	3,4	3,8	4,1	3,9	4,4	4,5	4,9	4,6	4,6	4,8	5
Реклама, Тыс. руб.	2,2	2,5	2,1	2,7	2,6	2,9	2,6	2,4	2,4	2,9	3,0	3,0

Построить трендовые модели расходов на рекламу и объема продаж. Определить взаимосвязь между факторами.

Лабораторная работа 4. Комплексный экономико-статистический анализ конкретного объекта или явления.

Самостоятельная работа: Самостоятельная работа студентов заключается в проведении комплексного экономико-статистического анализа конкретного объекта или явления Контрольная работа, написание эссе, составление алгоритма. Литература: обязательная - [2,7,10], 7 – стр.99 – 118, - дополнительная - [8, 9].

Для закрепления материала необходимо ответить на вопросы:

1. В чем состоит отличие между функциональной и стохастической связью.

2. Что представляет собой корреляционная связь.

3. Какими статистическими методами исследуются функциональные и корреляционные связи.

4. Какие показатели являются мерой тесноты связи между двумя признаками.

5. Какие основные задачи решаются с помощью корреляционного и регрессионного анализа.

6. В чем состоит значение уравнения регрессии. Метод определения параметров уравнения регрессии.

7. Какими показателями измеряется теснота корреляционной связи.

8. Какое значение имеет коэффициент детерминации, что такое коэффициент эластичности.

9. Какие непараметрические методы применяют для моделирования связи.

Задания для текущего тестирования

1. Корреляционная зависимость – это зависимость, при которой:

а) при изменении факторного признака изменяется результативный признак; б) при изменении факторного признака изменяется среднее значение результативного признака.

2. Функциональная зависимость – это:

а) одному значению аргумента соответствует одно и только одно значение функции; б) одному значению аргумента соответствует множество значений функций.

3. Цель корреляционно-регрессионного анализа заключается:

а) в оценке тесноты взаимосвязи;

б) в определении формы взаимосвязи;

в). в определении уравнения тренда.

4. Корреляционный анализ используется для изучения …

а. структуры явлений б. взаимосвязи явлений

в. развития явления во времени

5. Если на результативный признак влияют два факторных, то при проведении коррелционно - регрессионного анализа стоят модели:

а. сложные; б. парные; в. многофакторные; г. однофакторные

6. По направлению связи в статистике классифицируются на :

а. линейные и нелинейные б. закономерные и произвольные

в. сильные и слабые г. прямые и обратные

7. По аналитическому выражению связи классифицируются на:

а. линейные и криволинейные б. прямые и обратные

в. закономерные и произвольные г. сильные и слабые

8. Оценка значимости регрессии осуществляется на основе

а. коэффициент эластичности

б. средней квадратической ошибки

в. коэффициента детерминации

г. биссернального коэффициента корреляции

9. Для определения тесноты нелинейной связи между признаками используется:

а. корреляционное отношение

б. коэффициент контингенции

в. коэффициент взаимной сопряженности

г. коэффициент ассоциации

10. Частный коэффициент корреляции показывает тесноту…

а. связи между результативным признаком и остальными, включенными в модель; б. линейной зависимости между двумя признаками на фоне действия остальных, входящих в модель; в. линейной зависимости между двумя признаками при исключении влияния остальных, входящих в модель;

г. нелинейной зависимости

11. Укажите критерии, позволяющие проверить адекватность регрессионной модели:

а. критерий Стьюдента

б. коэффициент эластичности

в. средняя относительная ошибка аппроксимации

г. коэффициент детерминации

12. Критерии, позволяющие проверить адекватность регрессионной модели:

а. критерий Стьюдента

б. коэффициент эластичности

в. средняя относительная ошибка аппроксимации

г. коэффициент детерминации

13. После расчета неизвестных параметров модели регрессии следует

а. оценить адекватность и точность модели

б. выбрать функцию, связывающую результативный и факторный признаки

в. рассчитать интервальные прогнозные оценки

г. определить состав включаемых в модель регрессии переменных

14. Оценка тесноты связи при линейной форме связи производится с помощью:

а) коэффициента корреляции; б) корреляционного отношения;

в) коэффициента детерминации.

15. Оценка тесноты связи при любой форме связи производится с помощью:

а) коэффициента корреляции;

б) корреляционного отношения;

в) коэффициента детерминации.

16. Оценка тесноты связи между факторными и результативными признаками происходит с помощью:

а) коэффициента корреляции;

б) корреляционного отношения;

в) коэффициента детерминации.

17. Для определения тесноты связи между качественными признаками применяются коэффициенты:

а. корреляции Спирмена, б. контингенции

в. эластичности г. ассоциации

18. Если коэффициент корреляции равен единице, то зависимость:

а) функциональная; б) корреляционная.

19. Если коэффициент корреляции равен –0.7, то зависимость:

а) прямая; б) обратная.

20. Если значение коэффициента корреляции равно 0.8, то связь между признаками: а. заметная; б. слабая; в. умеренная; г. тесная

21. Коэффициент эластичности между числом студентов и стульями в соседней аудитории: а. близок к 1 б. имеет отрицательный знак

в. стремится к бесконечности г. близок к 0

22. Перекрестная эластичность двух товаров близка к нулю. Это могут быть товары: а. пиво и лимонад б. библия и виски в. мясо и сыр г. столы и стулья