Требуется рассчитать: Показатели центра распределения, квартили. Показатели вариации, показатели формы распределения. 3.Сделать выводы.

Задание 2. Имеются данные о распределении населения Российской Федерации по размеру среднедушевых денежных средств за 1998 год.

Среднедушевой доход, тыс. руб.	Численность населения в 1998 г., млн чел.
До 400	22,1
400-600	32,3
600-800	26,4
800-100	18,8
1000-1200	12,7
1200-1600	14,3
1600-2000	6,5
Свыше 2000	6,5
Всего	139,6

Определить: Показатели центра распределения. Коэффициент вариации. Децильный коэффициент дифференциации доходов. Определить степень концентрации доходов у отдельных групп населения (коэффициент Джини).

Задание 3. Имеются данные о ценах на товар А на рынках города, руб.

Рынок 1	10	15	20	17	12	15	15	15	20
	20	17	12	15	20	17
Рынок 2	20	25	25	20	18	17	20	18	20
Рынок 3	15	15	20	17	17	20	20	15	18
	17	18	25	20	15	18

Найти: внутригрупповые дисперсии; среднюю из внутригрупповых дисперсий; межгрупповую дисперсию; общую дисперсию.

Оценить вариацию цен за счет группировочного признака и за счет остальных факторов с помощью коэффициента детерминации.

Задание 4. Имеются следующие данные о расходах фонда занятости, связанных с содержанием службы занятости.

Уровень безработицы в %	1 – 1.8	1.8 – 2.6	2.6 – 3.4	3.4 – 4.2	4.2 - 5	5 – 5.8	Итого
Расходы, млн руб.	19.1	25.4	23.0	24.3	20.0	25.5	137.3

Провести статистический анализ ряда распределения.

Задание 5. Туристическая компания "Эгна" за 2008 год распродала путевки в разные страны по цене от 200 до 1800 долларов. Данные распределились следующим образом.

Цена путевки, долл.	200-400	400-600	600-800	800-1000	1000-1200	1200-1400	1400-1600	1600-1800	Всего
Количество	11	23	36	42	28	17	9	4	170

Провести статистический анализ ряда распределения

Лабораторная работа 2. Комплексный анализ ряда распределения.

Самостоятельная работа студентов по теме предполагает: написание контрольной работы, написание эссе, составление кроссворда, алгоритма, статистического исследования двух предприятий.

Теоретическая основа, практические задачи, подробные методические рекомендации приводятся в литературе: обязательная - [2,7,10], 7 – стр.64 – 79, - дополнительная - [8, 9].

Для закрепления материала необходимо ответить на вопросы:

1. Что представляет собой вариация признака?

2. Что такое вариационный ряд распределения?

3. Какие вариационные ряды распределения Вы знаете?

4. Что такое мода для дискретного ряда?

5. Что такое медиана для дискретного ряда?

6. Как определить моду для интервального ряда?

7. Как определить медиану для интервального ряда?

8. Какие показатели входят в показатели центра распределения?

9. Назовите основные показатели, характеризующие форму распределения.

10. Как графически можно интерпретировать показатели асимметрии и эксцесса?

11. Какие показатели вариации Вы знаете?

12. Какие абсолютные и относительные показатели вариации Вы знаете?

Задания для текущего тестирования

1. Ряд распределения  это:

а) последовательность одноименных показателей, расположенных в хронологическом порядке;

б) упорядоченные данные, разбитые на несколько групп по возрастанию или убыванию анализируемого признака;

2. Вариационные ряды могут быть:

а) дискретными и интервальными;

б) вариационными и атрибутивными;

в) количественными и качественными.

3. Параметрами ряда распределения являются:

а) варианта; б) частота и мода; в) варианта и частота.

4. Моду и медиану рассчитывают по формуле для:

а) интервального ряда; б) дискретного ряда; в) динамического ряда.

5. Мода, медиана и среднее арифметическое – это …

а) показатели формы распределения; б) показания центра распределения;

в) показатели вариации.

6. Отношение частоты признака к объему совокупности  это:

а) частота; б) частость; в) накопленная частота.

7. Медианный интервал представляет собой:

а) интервал, содержащий наибольшую частоту;

б) интервал, для которого выполняется соотношение: первая накопленная частота равна или больше половины суммы всех частот.

8. Модой ряда распределения является:

а) наибольшая частота; б) наибольшая варианта;

в) варианта, которая чаще других встречается;

г) варианта, делящая ряд на две равные части.

9. Модальный интервал представляет собой:

а) интервал, содержащий наибольшую частоту;

б) интервал, содержащий наибольшую варианту.

10. Размах вариации - это:

а) максимальное значение признака в исходном ряду;

б) минимальное значение признака в исходном ряду;

в) разность между максимальным и минимальным значениями признака исходного ряда.

11. Какой (какие) из показателей вариации, перечисленных ниже, является относительным показателем?

а) размах вариации; б) среднее линейное отклонение; в) дисперсия;

г) среднее квадратичное отклонение; д) коэффициент вариации.

12. Если коэффициент вариации изменяется от 10% до 25%, то вариация:

а) слабая; б) сильная; в) умеренная;

13. Степень отклонения распределения частот от симметричной формы характеризуется:

а) вариацией; б) асимметрией.

14. Асимметрия, эксцесс – это показатели …

а) формы распределения; б) структуры распределения; в) вариации.

15. Какие показатели являются показателями формы распределения:

а) размах вариации; б) дисперсия; в) асимметрия; г) эксцесс.

16. Если выполняется равенство М₀ = М_е =Х , то распределение:

а) асимметричное; б) симметричное.

17. Асимметрия правосторонняя, если

а) ; б) ; в) .

18. При отсутствии различия между значениями признака внутри отдельных групп дисперсия групповых средних равна:

а. общей дисперсии, б. межгрупповой дисперсии,

в. нулю, г. единице, д. внутригрупповой дисперсии

19. Вариацию изучаемого признака, возникающую под влиянием фактора, положенного в основу группировки, характеризует … дисперсия.

а. межгрупповая, б. внутригрупповая, в. общая

20. Межгрупповая дисперсия составляет 61% от общей дисперсии. Эмпирическое корреляционное отношение = …(с точностью до 0,01)

а. 0,78, б. 1.21

21. Коэффициент детерминации может принимать значения…

а. от -1 до 0, б. от 0 до 1,

в. любые положительные, г. любые меньше нуля, д. от -1 до 1

22. Коэффициент детерминации представляет собой долю…

а. межгрупповой дисперсии в общей,

б. дисперсии теоретических значений в остаточной дисперсии,

в. дисперсии теоретических значений в общей дисперсии,

г. межгрупповой дисперсии в остаточной

23. Для симметричных распределений рассчитывают показатель эксцесса. Кто первый его рассчитал?

а) Пирсон; б) Линдберг; в) Пуассон.

24. Смещение вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения называется:

а) асимметрией; б) симметрией; в) эксцессом.

25. Смещение вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения называется:

а) асимметрией; б) симметрией; в) эксцессом.

Выборочное наблюдение

Программа

Выборочное наблюдение как важнейший источник статистической информации. Генеральная и выборочные совокупности, их обобщающие характеристики. Репрезентативность выборки. Повторный и бесповторный отборы. Средняя и предельная ошибка выборки. Определение необходимой численности выборки. Доверительные интервалы. Виды выборки.

Комбинирование различных способов отбора и оценка результатов выборки. Понятие о малой выборке, определение ошибок при малой выборке.

Применение выборочного наблюдения в экономических и социальных исследованиях.

Выборочным называется такое наблюдение, при котором характеристика всей совокупности единиц дается по некоторой части единиц, отобранных в случайном порядке. Вся изучаемая совокупность единиц называется генеральной совокупностью. Численность единиц генеральной совокупности обозначается N. Часть совокупности, которая в случайном порядке выбирается из генеральной совокупности, называется выборочной совокупностью. Число единиц в выборочной совокупности обозначается n.

Необходимость выборочного наблюдения обусловлена следующими причинами:

 иногда выборочное наблюдение - единственно возможное статистическое наблюдение (изучение продолжительности горения лампочки);

- выборочное наблюдение требует меньше времени, труда, а, следовательно, и денег по сравнению со сплошным наблюдением;

- при выборочном наблюдении совершается меньше ошибок, поэтому информация более достоверна;

- выборочное наблюдение используется для контроля результатов сплошного наблюдения.

Основное условие проведения выборочного наблюдения: отбор единиц из генеральной совокупности в выборочную должен производиться в случайном порядке. Это условие обеспечивает объективность результатов, т.е. независимость результатов от лиц, производящих отбор.

Исходная статистическая совокупность может изучаться по количественному и альтернативному признаку. Если признак количественный, обобщающими характеристиками генеральной совокупности являются генеральная средняя и генеральная дисперсия.

Аналогично, обобщающими характеристиками выборочной совокупности являются выборочная средняя и выборочная дисперсия.

Если совокупность изучается по альтернативному признаку, то характеристикой генеральной совокупности является доля единиц. При изучении качества продукции определяют относительную долю тех единиц, которые не выдерживают установленного стандарта качества, т.е. относятся к браку. Доля единиц в генеральной совокупности: - генеральная доля. Доля единиц в выборочной совокупности: - выборочной доля (частость).

При проведении выборочного наблюдения даже теоретически нельзя получить абсолютно точные данные, как при сплошном наблюдении. Это обусловлено тем, что обследованию подвергается не вся совокупность, а только ее часть. Поэтому при проведении выборочного наблюдения неизбежна некоторая погрешность, ошибка.

Ошибки, свойственные выборочному наблюдению, называются ошибками репрезентативности, т.е. представительства. Они характеризуют величину расхождения между данными выборочного наблюдения и всей совокупности.

Ошибки репрезентативности делятся на случайные и систематические. Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения. Случайные ошибки возникают потому, что выборочная совокупность недостаточно точно воспроизводит всю совокупность из-за не сплошного характера наблюдения.

В зависимости от способа отбора единиц из генеральной совокупности в выборочную различают повторный и бесповторный отбор.

При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после того, как некоторая единица была отобрана, она снова возвращается в генеральную совокупность и снова может быть выбранной. При бесповторном отборе единицы после отбора и регистрации изучаемого признака в генеральную совокупность не возвращаются. Вероятность попадания отдельных единиц в выборку все время изменяется. При соблюдении принципа случайного отбора ошибка выборки зависит от численности выборки. Чем больше численность выборки при прочих равных условиях, тем меньше величина ошибки выборки.

Ошибка выборки определяется также степенью варьирования изучаемого признака, а степень варьирования характеризуется в статистике средним квадратом отклонений - дисперсией или величиной р(1-р) (для альтернативного признака). При одинаковой численности выборочной совокупности ошибка выборки будет меньше в той совокупности, которая отобрана из генеральной совокупности с меньшей изменчивостью изучаемого признака.

Ошибка выборки - это абсолютная величина разности между соответствующими характеристиками выборочной и генеральной совокупности. - ошибка для средней. - ошибка для доли. Как и сама выборочная характеристика, ошибка выборки является случайной величиной. Пользуясь теоремой Ляпунова, можно указать вероятность Р того, что ошибка выборки не превысит некоторую заданную величину . Вероятность Р при этом называют доверительной вероятностью, а пределы, в которых с этой вероятностью может находиться генеральная характеристика, называют доверительными пределами или границами генеральной характеристики.

Наиболее простым является расчет ошибки выборки при так называемом повторном случайном отборе, при котором отобранная единица после обследования возвращается в генеральную совокупность и вновь участвует в отборе на равных основаниях с другими единицами.

Средняя ошибка выборки для количественного признака имеет вид:

отбор повторный: , где - ошибка выборочной средней; - дисперсия варьируемого признака в генеральной совокупности; n - численность единиц выборочной совокупности. В практических расчетах вместо генеральной дисперсии используют выборочную;

отбор бесповторный: , где - доля единиц, отобранных в выборку (процент выборки); N - численность единиц генеральной совокупности.

Средняя ошибка выборки для альтернативного признака имеет вид:

отбор повторный: .

отбор бесповторный:

Средняя ошибка выборки показывает, какие возможны отклонения характеристик выборочной совокупности от соответствующих характеристик генеральной совокупности. Однако о величине этой ошибки можно судить с определенной вероятностью. На величину вероятности указывает множитель t – коэффициент доверия. Величину t в функции Лапласа называют предельной ошибкой выборки. Обозначив предельную ошибку выборки , получим для количественного признака .

Предельная величина разности между частостью и долей (предельная ошибка выборки для альтернативного признака) определяется по следующему выражению . Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности и величину предельной ошибки этой средней , которая показывает (с определенной вероятностью), насколько выборочная средняя может отличаться от генеральной средней в большую или меньшую сторону. В этом случае величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна: ( ), верхняя граница: ( ).

Доверительный интервал:

- для генеральной средней ,

- для генеральной доли: .

Приведенные формулы для определения величины ошибки выборки дают возможность не только определять эти ошибки, но и предварительно рассчитать, какую необходимо взять численность выборки, чтобы ошибка не превышала заданных размеров.

В практике при проектировании выборочного наблюдения всегда заранее определяют его численность. Для этого необходимо с определенной вероятностью задать уровень точности выборочной совокупности и на основании формулы предельной ошибки выборки рассчитывают численность выборочной совокупности. Так, для количественного признака при повторном отборе объем необходимой численности выборки можно получить путем преобразования формулы:

. Отсюда: .

Таким образом, необходимая численность выборки при измерении средней для повторного отбора равна дисперсии, деленной на квадрат заданной точности. Под точностью понимается допустимая ошибка выборки.

При определении необходимой численности выборочного обследования по приведенным формулам возникает затруднение, т.к. мера варьирования признака или его доля заранее неизвестны и будут определены лишь после проведения выборочного обследования. Между тем, без этих величин нельзя определить необходимую численность выборки.

На практике поступают следующим образом: вместо  или w подставляют приближенное значение, полученное из предыдущих обследований или на основе каких-либо пробных выборочных наблюдений.

При этом исходят из того, что чем больше величина  или чем ближе доля признака приближается к 0.5, тем большую численность выборки необходимо взять при той же заданной точности. Поэтому для предосторожности при всякого рода сомнениях принимают наибольшее значение из этих величин.

Пример 1. В цехе завода имеется 2000 рабочих. Для определения затрат времени на изготовление одной детали проведено выборочное обследование. Установлено, что среднее квадратическое отклонение затрат рабочего времени на изготовление одной детали составляет 10 минут. Определить, какое количество рабочих необходимо отобрать, чтобы с вероятностью 0.954 ошибка выборки не превышала 2-х минут. 1.Отбор повторный. 2.Отбор бесповторный.

Решение. Численность единиц генеральной совокупности (численность рабочих завода) N составляет 2000 человек. Необходимо найти число единиц в выборочной совокупности (количество рабочих в выборке) для повторного и бесповторного отбора. Исходная статистическая совокупность изучается по количественному признаку. В зависимости от способа отбора единиц из генеральной совокупности в выборочную различают повторный и бесповторный отбор.

При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, т.к. после того, как некоторая единица была отобрана, она снова возвращается в генеральную совокупность и снова может быть выбрана. Ошибка выборки также определяется степенью варьирования изучаемого признака, который характеризуется в статистике средним квадратическим отклонением.

В задании определена величина среднего квадратического отклонения  = 10 мин., из которого можно получить величину дисперсии . В исходных данных приведено значение предельной ошибки выборки – 2 минуты.

Предельная ошибка выборки вычисляется по формуле: , где t - коэффициент доверия, который определяется в зависимости от заданной вероятности Р по таблицам Лапласа. При заданной вероятности Р = 0.954, коэффициент доверия t = 2. В формуле предельной ошибки выборки - средняя ошибка выборки, которая для повторного отбора определяется по формуле: , где - дисперсия варьируемого признака в генеральной совокупности; n - численность единиц выборочной совокупности. Учитывая, что предельная ошибка выборки =2, можно рассчитать среднюю ошибку выборки: = 2 : 2 = 1 (мин.).

Находим численность выборки n при повторном отборе, исходя из формулы средней ошибки выборки ; исходя из предельного значения ошибки выборки . Таким образом, при повторном отборе, чтобы с вероятностью 0.954 ошибка выборки не превышала 2-х минут, необходимо отобрать из генеральной совокупности 100 рабочих.

При бесповторном отборе единицы после отбора и регистрации изучаемого признака в генеральную совокупность не возвращаются. Численность генеральной совокупности N уменьшается, вероятность попадания отдельных единиц в выборку все время изменяется.

При бесповторном отборе средняя ошибка выборки вычисляется по формуле: , где - доля единиц, отобранных в выборку (процент выборки); N - численность единиц генеральной совокупности.

Исходя из формулы предельной ошибки выборки, необходимая численность выборки при бесповторном отборе будет равна:

.

Таким образом, при бесповторном отборе, чтобы с вероятностью 0.954 ошибка выборки не превышала 2-х минут, необходимо отобрать из генеральной совокупности 95 рабочих.

В практике статистических исследований в последнее время часто приходится иметь дело с небольшими по объему выборками (исследование деятельности малых и средних предприятий, коммерческих банков, фермерских хозяйств). Под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 10.

Разработка теории малой выборки была начата английским ученым Госсетом (псевдоним Стьюдент), в которой он доказал, что оценка расхождения между средней малой выборки и генеральной средней имеет особый закон распределения.

Для определения возможных пределов ошибки пользуются критерием Стьюдента: , где - мера случайных колебаний выборочной средней в малой выборке. Величина  вычисляется на основе данных выборочного наблюдения. Она равна 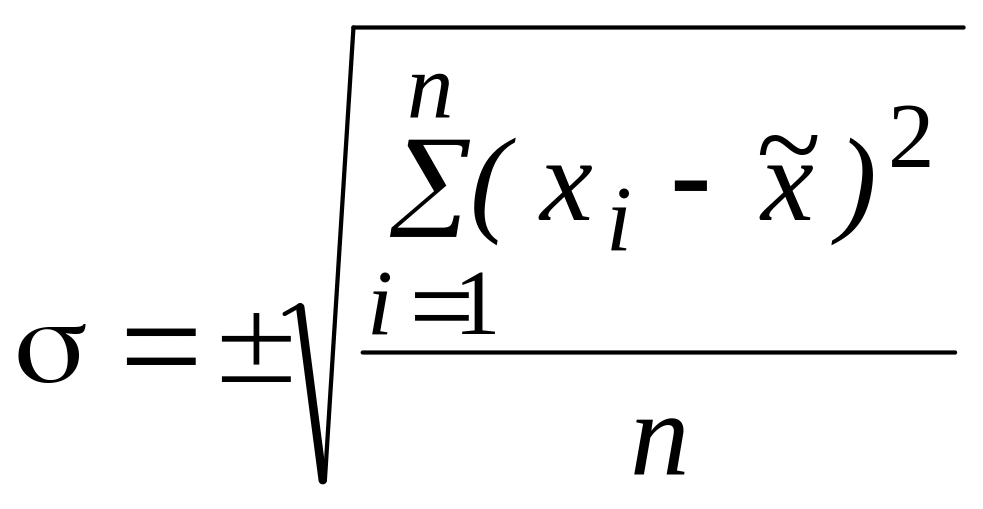. Данная величина используется лишь для исследуемой совокупности, а не в качестве приближенной оценки  в генеральной совокупности.

При небольшой численности выборки распределение Стьюдента отличается от нормального: большие величины критерия имеют здесь большую вероятность, чем при нормальном распределении. Предельная ошибка малой выборки в зависимости от средней ошибки может быть представлена: . В малых выборках величина коэффициента доверия вычисляется несколько иначе, чем при больших выборках. Существуют специальные таблицы Стьюдента, по которым определяется коэффициент доверия.

В статистике применяются различные способы формирования выборочных совокупностей. Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.

Практика применения выборочного метода в экономико-статистических исследованиях использует следующие способы отбора единиц из генеральной совокупности: индивидуальный отбор, групповой отбор, комбинированный отбор. Различные формы организации выборочного наблюдения представлены ниже.

1. Собственно случайный отбор (лотерея, жеребьевка). Выборочная совокупность образуется в результате случайного отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц определяется, исходя из принятой доли выборки. Собственно случайный отбор может быть повторным и бесповторным.

2. Нерайонированный и районированный отбор. При районированном отборе генеральная совокупность разбивается на группы и из каждой группы отбираются отдельные единицы (предприятия разбиваются по отраслям и от каждой отрасли отбирается определенный процент предприятий). Районированный отбор всегда бесповторный. При нерайонированном отборе генеральная совокупность на группы не разбивается. Нерайонированный отбор может и повторным, и бесповторным.

3. Механический отбор. Генеральная совокупность упорядочивается по определенному (нейтральному) признаку, а затем через определенные интервалы выбираются единицы в выборочную совокупность (фамилии студентов упорядочиваются по алфавиту, а затем упорядочивается каждый пятый, десятый студент с интервалом в пять единиц). Механический отбор всегда бесповторный.

4. Типический отбор. Применяется для качественно разнородной генеральной совокупности. Сначала производят типологическую группировку единиц генеральной совокупности (разбивают ее на качественно однородные совокупности), затем из образованных групп производят отбор.

5. Серийный отбор. При серийном отборе единицы отбираются сериями, например: 15, 100105 и т.д.

6. Многофазная выборка. Этот вид выборки проводится в несколько этапов. Все предприятия отрасли исследуются по сокращенной программе, затем из всех выбирается каждое пятое предприятие отрасли и изучается по более развернутой программе, затем изучается каждое десятое предприятие отрасли и описывается детально.

7. Многоступенчатый отбор. Проводится в несколько ступеней, на каждой из них своя единица отбора. Например, при обследовании бюджета населения, доходов и расходов все семьи распределяются по областям, из всех областей выбираются 15 (единица отбора - область); для каждой отобранной области отбираются населенные пункты (единица отбора - населенный пункт); для каждого отобранного населенного пункта отбираются семьи (единица отбора - семья).

Таким образом, способы формирования выборочной совокупности выступают в качестве важнейшего фактора, который определяет репрезентативность выборочного обследования.

Пример 2. При изучении покупательского спроса произведено 10%-ное выборочное обследование продажи игрушек. При случайном способе отбора получены следующие данные распределения игрушек по возрастному признаку.

Возраст детей	До 3-х лет	36	69	912	1215	Свыше 15	Всего
Кол - во игрушек	147	155	180	130	138	125	875

Определить: с р = 0.954 возможные пределы значений доли продажи игрушек для детей от 3-х до 15-ти лет; с р = 0.997 возможные пределы значения среднего возраста детей, для которых покупаются игрушки.

Решение. При случайном способе отбора выборка может быть повторной и бесповторной.

1. Доля продажи игрушек - альтернативный признак; возможные пределы значений доли продажи игрушек - доверительный интервал для альтернативного признака , где w - частость.

.

- предельная ошибка выборки, где t - коэффициент доверия, находится по таблицам Лапласа. При вероятности 0.954 коэффициент доверия равен 2. - средняя ошибка выборки для альтернативного признака. Средняя ошибка выборки для альтернативного признака при повторном отборе имеет вид: , =  0.015; при бесповторном отборе: , где - доля единиц, отобранных в выборку; N - численность единиц генеральной совокупности. = 0.0148.

Предельная ошибка выборки при повторном отборе: = 2(0.015) = 0.03; при бесповторном отборе: = 2(0.0148) = 0.0296.

Доверительный интервал для генеральной доли:

- при повторном отборе: ;

- при бесповторном отборе: .

Вывод: с вероятностью 0.954 можно утверждать, что возможные пределы доли продажи игрушек будут находиться в генеральной совокупности при повторном отборе от 65% до 71%, при бесповторном отборе – от 65.78% до 72.02%.

2. Значение среднего возраста детей – количественный признак. Возможные пределы значения среднего возраста детей в генеральной совокупности будут определяться из доверительного интервала: , где 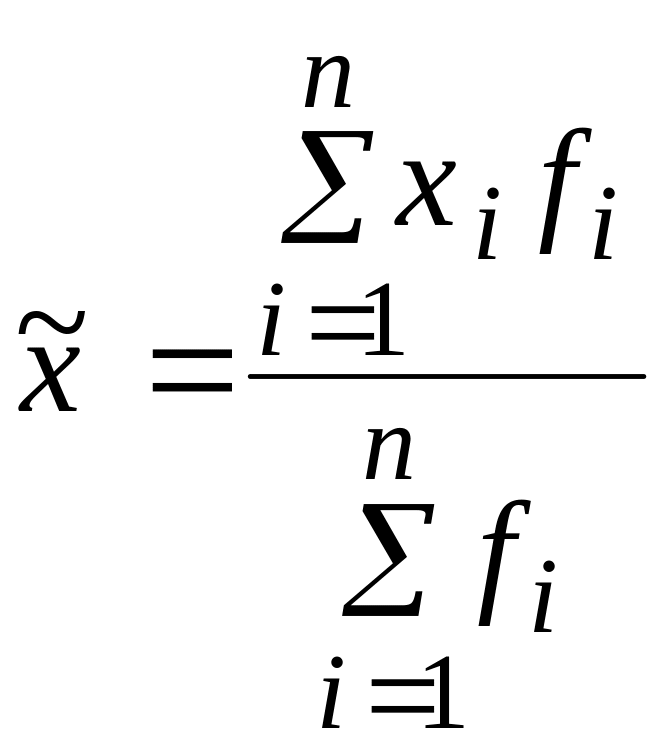- выборочная средняя; - предельная ошибка выборки для количественного признака; t - коэффициент доверия (при вероятности 0.997 коэффициент доверия равен 3); - средняя ошибка выборки.

Средняя ошибка выборки для количественного признака имеет вид: при повторном отборе: , где - дисперсия варьируемого признака в генеральной совокупности; n - численность единиц выборочной совокупности; при бесповторном отборе: . Для нахождения выборочной средней и дисперсии составим рабочую таблицу.

Возраст детей	Кол - во игрушек	x	xf
0 – 3 3 – 6 6 – 9 9 – 12 12 – 15 15 – 18 Всего	147 155 180 130 138 125 875	1.5 4.5 7.5 10.5 13.5 16.5 	220.5 697.5 1350 1365 1863 2062.5 7558.5	7.5 4.5 1.5 1.5 4.5 7.5 	1102.5 697.5 270 195 621 937.5 3823.5	8268.75 3138.75 405 292.5 2794.5 7031.25 21930.75

Средний возраст детей, для которых покупают игрушки в выборке составляет: = 7556.5 : 875 = 9 лет.

Дисперсия 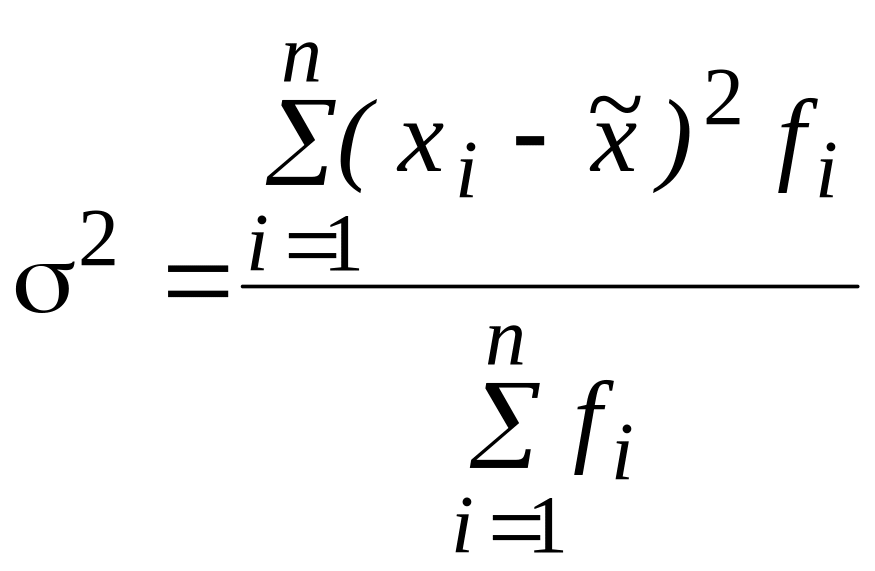= 21930.75 : 875 = 25.06  25.

Средний возраст детей в генеральной совокупности будет находиться в пределах .

При повторном отборе: ; .

При бесповторном отборе: ; .

Вывод: с вероятностью 0.997 можно утверждать, что средний возраст детей в генеральной совокупности будет колебаться при повторном отборе от 8.52 до 9.48 лет; при бесповторном отборе от 8.55 до 9.45 лет.

Лекция 7. Тема «Выборочное наблюдение» (ВН) является одной из центральных в курсе статистики. Это обусловлено взаимосвязью данной темы с другими темами данного курса, высшей математики и теории вероятностей. Поэтому освоение теоретического материала, умение правильно решить практические задачи, грамотно интерпретировать полученные результаты служат необходимым условием успешного изучения статистики. Теоретическая основа темы обусловлена практическими вопросами, требующими своего решения при организации выборочного наблюдения и анализе его результатов. Таким вопросами являются определение способа отбора и процедуры выборки, вычисление ошибок выборки и построение доверительных интервалов; определение необходимой численности выборки.

Практическое занятие 5. Решение задач по теме.

Задание 1. При изучении покупательского спроса произведено 5%-е выборочное обследование продаж картин известного художника. При случайном способе отбора получены следующие данные о распределении проданных картин по цене.

Цена, руб.	До 300	300 - 500	500 - 700	700 - 900	900 и выше	Всего
Число картин	47	22	15	10	6	100

На основе данных выборочной совокупности определить для генеральной совокупности:

- с вероятностью 0.954 возможные пределы значений доли продажи картин по цене от 300 до 700 рублей;

- с вероятностью 0.997 возможные пределы значения средней цены картин.

Задание 2. При изучении уровня безработицы среди различных групп населения города Нижнего Новгорода было проведено 5%-е выборочное обследование. При случайном способе отбора в выборку взято 700 человек, из которых 120 оказались безработными. Средний возраст составил 28 лет, а среднее квадратическое отклонение ± 2 года. Определить:

- с р = 0.954 пределы, в которых находится генеральная доля безработных.

- с р = 0.997 пределы, в которых находится средний возраст опрошенных.

Задание 3. При проведении социологического опроса по вопросу о доверии депутату был проведен 10%-й выборочный опрос. При этом были получены следующие данные о доверии депутату в зависимости от возраста.

Возраст людей	До 20 лет	20 - 30	30 - 40	40 - 50	Свыше 50 лет	Всего
Кол-во человек	180	125	138	105	90	638

С вероятностью 0.997 определить значение среднего возраста людей в генеральной совокупности, которые доверяют данному депутату.

Задание 4. Из общего числа (30000) читателей библиотек города произведено выборочное обследование 3000 читателей, отобранных методом случайного бесповторного отбора.

Читатели	Группы читателей по количеству прочитанных книг, шт.			Итого
	500 - 600	600 - 700	700 - 800
Детектив	150	100	150	400
Романы	300	1500	200	2000
Приключения	200	200	200	600
Итого	650	1800	550	3000

Принимая во внимание, что произведена случайная выборка, определить для генеральной совокупности:

- с р = 0.997 возможные пределы среднего количества прочитанных книг;

- с р = 0.954 возможные пределы доли детективов среди прочитанных книг.

Задание 5. Обследование предпочтений телезрителей дало следующие результаты по возрастным группам аудитории двух сериалов "Бандитский Петербург" и "Граница", показанных на РТР и НТВ

Возраст	До 20	20-30	30-40	40-50	50-60	Свыше 60	Всего
ОРТ	9	14	23	29	19	6	100
НТВ	13	20	24	22	11	10	100

Определить для генеральной совокупности: с вероятностью 0.954 возможные пределы значений доли возрастной аудитории до 20 лет; с вероятностью 0.997 возможные пределы значений среднего возраста аудитории. Прокомментировать различия в среднем возрасте между двумя группами.

Самостоятельная работа: написание эссе, составление кроссворда, составление алгоритма.

Подробное изложение материала по теме представлено в основной литературе обязательная - [2,7,10], 7 – стр.80 - 98, - дополнительная - [8, 9].

Для закрепления теории необходимо ответить на основные вопросы:

1. В чем преимущество ВН по сравнению с другими методами статистического исследования.

2. Назовите этапы выборочного наблюдения.

3. Какие виды ошибок выборочного наблюдения вы знаете. Что такое ошибка репрезентативности.

4. В чем отличие ошибок выборки при повторном и бесповторном отборе.

5. Как определяются ошибки выборки для количественного и альтернативного признаков.

6. Как определяется предельная ошибка выборки для количественного признака.

7. Как определяется средняя ошибка выборки при определении генеральной доли при повторном и бесповторном отборе.

8. Какие факторы влияют на определение объема выборки при различных способах отбора.

9. Какие способы формирования выборочной совокупности вы знаете.

10. Какой вид выборочного наблюдения необходимо использовать, если генеральная совокупность не является однородной.

11. Назовите основные области применения выборочного метода.

Задания для текущего тестирования

1. Наблюдение, при котором характеристика всей совокупности единиц дается по некоторой части единиц, отобранных в случайном порядке:

а) сплошное наблюдение; б) выборочное наблюдение.

2. Если совокупность изучается по количественному признаку, то обобщающими характеристиками генеральной совокупности являются:

а) выборочная средняя; б) генеральная средняя;

в) выборочная дисперсия; г) генеральная дисперсия.

3. Если совокупность изучается по альтернативному признаку, то обобщающей характеристикой выборочной совокупности является:

а) число единиц совокупности, обладающих каким-либо признаком;

б) частость.

4. При какой вероятности коэффициент доверия t=1:

а) P= 0,954 б) P= 0,997 в) P= 0,683

5. Средняя ошибка выборки для доли брака 2%, доля брака в выборке – 3%. С какой вероятностью можно утверждать, что доля брака в генеральной совокупности не превышает 7%?

а) 0.683; б) 0.954; в) 0.997.

6. Для проверки качества товара, упакованного в ящики(коробки) целесообразно сформировать выборку:

а. механическую б. серийную в. собственно-случайную г. типическую

7. В случае отбора единиц в выборку из генеральной совокупности, разбитой на равные группы, получают выборку:

а. собственно-случайную б. типическую в. серийную г. механическую

8. Выборка, заключающаяся в отборе единиц из общего списка единиц генеральной совокупности способом жеребьевки называется:

а. типичной б. собственно случайной в. механической г. серийной

9. Укажите, к какой форме организации выборочного наблюдения относится следующее условие: "генеральная совокупность разбивается на группы, и из каждой группы отбираются отдельные единицы":

а) собственно случайный отбор б) нерайонированный отбор

в) районированный отбор г) механический отбор

10. Укажите метод отбора, при котором сохраняется вероятность попадания единицы генеральной совокупности в выборку:

а. повторный б. индивидуальный в. Групповой г. комбинированный

д. бесповоротный

11. Для сопоставления эффективности работы двух поликлиник города организовано наблюдение, оценивающее количество обращений к терапевту и время обслуживания пациентов. Для этого 10 % пациентов случайно отобраны из всех прикрепленных к поликлинике по каждой букве алфавита, с которой начинается фамилия. Назовите способ организации выборки:

а.серийный б.комбинированный в.механический г.собственно-случайный

12. При отборе отдельных единиц генеральной совокупности в выборочную используется отбор:

а. типический б. групповой в. повторный г. индивидуальный

13. Какие ошибки возникают в результате того, что нарушается принцип отбора единиц в выборочную совокупность:

а) систематические; б) случайные.

14. В зависимости от способа отбора единиц в выборку различают:

а) повторный отбор; б) бесповторный отбор.

15. Расхождение между расчетными значениями признака в выборочной совокупности и действительными значениями признака в генеральной совокупности – это

а. ошибка регистрации б. ошибка репрезентативности

в. ошибка вычислительного устройства г. ошибка метода расчета

16. Расхождение между полученными значениями в ходе наблюдения и действительным значением изучаемых величин называется:

а. ошибкой регистрации б. ошибкой наблюдения

в. ошибкой репрезентативности г. ошибкой аппроксимации

17. Репрезентативность результатов выборочного наблюдения зависит от …

а. объема выборки б. определения границ объекта исследования

в. времени проведения наблюдения

г. вариации признака д. продолжительность проведения наблюдения

18. Объем генеральной совокупности не меняется на протяжении всего процесса выборки при … методе отбора. а. повторном б. бесповторном

19. При уменьшении численности выборки предельная ошибка выборки …

а. возрастает б. падает

20. Средняя ошибка случайной повторной выборки … , если ее объем увеличить в 4 раза

а. не изменится б. уменьшится в 2 раза

в. уменьшится в 4 раза г. увеличится в 4 раза

21. Теорема Бернулли рассматривает ошибку выборки для:

а) альтернативного признака б) количественного признака

22. Согласны ли вы с тем, что под малой выборкой понимается такое выборочное наблюдение, численность единиц которого не превышает 10:

а) да; б) нет

23. Теорию малой выборки разработал ученый:

а) Лаплас б) Бернулли в) Госсет г) Ляпунов

24. Объем повторной случайной выборки увеличится в … раза, если среднее квадратическое отклонение увеличится в 2 раза. а. 2 б. 4

25. Дисперсия = …(с точностью до 0,0001), если при осмотре 200 деталей среди них оказалось 10 бракованных изделий а. 0,0475 б. 0,475