3.3. Определяем допускаемые напряжения изгиба.
Допускаемые напряжения изгиба при расчете на усталость определяются по формуле:
.
В предложенной формуле не учитывается ряд коэффициентов, равных или близких к единице.
- предел выносливости зубьев по напряжениям
изгиба табл. 8.8(с. 176,[5]) для шестерни будет
равен:
МПа,
а для колеса (п.3.1)
МПа.
Редуктор нереверсивный (односторонняя нагрузка), тогда
.
Коэффициент
долговечности YNдля
шестерни, т.е. при Н>350НВи
нешлифованной поверхностью зубьев
и
,
но
.
В
данном случае при
коэффициент
,
а если
,
то
.
Рекомендуется принимать для всех сталей
.
При типовых режимахнагружения
,
где по табл. 8.9 (с.181[5]) для режима II и термообработки – азотирование для шестерни
а для колеса – улучшение и режим II, коэффициент
,
а NKуже вычислено (п.3.2), т.е.
,
а для колеса
,
т.е.
и
,
и
,
следовательно
.
Коэффициенты безопасности по табл. 8.8 [5] следующие:
.
Допускаемые напряжения изгиба для шестерни
МПа,
а для колеса
МПа.
3.4. Определяем предельные допускаемые напряжения для расчетов статической прочности зубьев при кратковременных нагрузках.
Кратковременные перегрузки, не учтенные при расчете на усталость, могут привести к потере статической прочности зубьев. Поэтому необходимо проверить статическую прочность при перегрузках.
Контактные напряжения.
Максимальные допускаемее контактные напряжения (с.183, [5]) при азотировании, т.е. для шестерни
МПа≤
2000
МПа,
а для колеса при улучшении
МПа.
Напряжение изгиба.
Максимальные допускаемые напряжения изгиба (с.183, [5])
,
где
при m=
9(
и азотирование) для шестерни предельное
значение коэффициента долговечности
,
коэффициент учета частоты приложения пиковой нагрузки
и коэффициент запаса прочности рекомендуется назначать
и
МПа (п. 3.3), тогда
МПа.
При
m=
6 (
и улучшение), т.е. для колеса
,
,
тогда
МПа
(п. 3.3)
МПа.
3.5. Определяем межосевое расстояние.
Межосевое расстояние определяем по формуле (с.156, [5]):
, (3.1)
где приведенный модуль материала шестерни и колеса (сталь 40Х)
МПа.
По табл. 8.4 (с. 143 [5]) при Н2>350HB и H3≤ 350 HB и при симметричном расположении колеса относительно опор принимаем коэффициент его ширины
.
По формуле (8.12, с. 112[5])
.
Коэффициент
распределения нагрузки между зубьями
при степени точности их изготовления
для косозубых передач (с. 133, [5]):
,
где
С = 0,25 приH3≤ 350 HB,
тогда
.
Так
как
,
то принимается
.
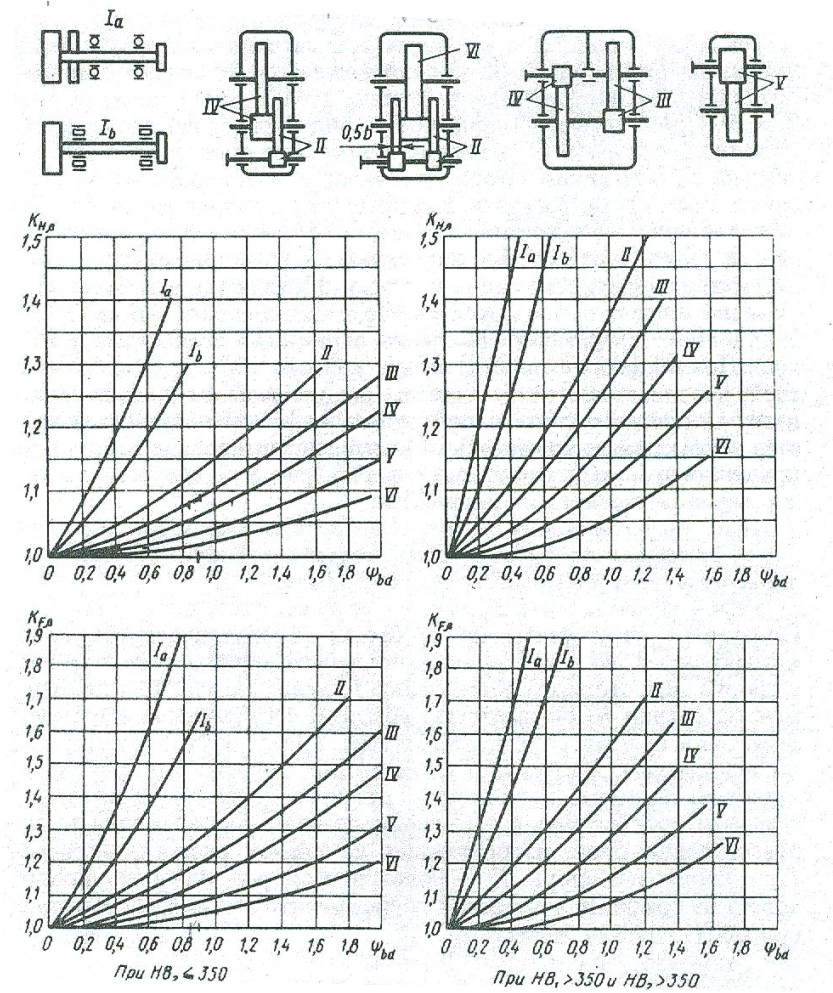
Коэффициент
концентрации нагрузки (с.136, [5]) при
и
по графику IV
.
Межосевое расстояние по формуле (3.1) будет равно:
мм.
где
Т3=1764,71 H·м= 1764,71·103 H·мм, (п.3)
[σH]3=731,94 МПа=731,94 H ⁄ мм2 (п.3.2)
Принимаем стандартное значение (с.143, [5]), т.е.
мм.
Коэффициент ширины колеса
,
тогда
мм.
По
табл. 8,5 (c. 144, [5]) (принимаем ψm=
45…30 или 30…20) принимаем ψm
= 25,
с
другой стороны
и модуль зацепления
мм.
По ГОСТу выбираем (табл. 8.1 [5])
мм,
Окружной модуль mtпри косозубой передаче
,
где β – угол наклона зубьев шестерни и колеса.
Определяем угол β по формуле (8.23) (с. 153 [5]), принимая коэффициент осевого перекрытия (с. 153 [5]) εβ = 1,2 (рекомендуется εβ = 1,1), тогда
,
.
Графики коэффициента концентрации нагрузки, [5].
Рекомендуется принимать β = (8º…20º).
Так как межосевое расстояние
,
то суммарное число зубьев шестерни и колеса будет равно:
.
Принимаем
.
Известно также, что передаточное число
или
,
тогда
,
а
.
Принимаем
.
Следовательно,
передача без смещения (при нарезании
колес со смещением делительная плоскость
рейки смещается к центру или от центра
заготовки, если
).
Число зубьев колеса
.
Фактическое передаточное число
и при
Другое фактическое передаточное число
,
где
(п. 1.6).
Уточняем величину β по межосевому расстоянию, т.е.
,
тогда
и
.
Рекомендация (8º ≤ β ≤ 20º) выполняется.
У передач без смещения диаметры начальных и делительных окружностей совпадают, т.е. для шестерни
мм,
а для колеса
мм,
где
мм.
Размеры зубьев шестерни и колеса: высота головки зуба
мм,
высота ножки зуба
мм,
высота зуба
мм.
Для шестерни без смещения:
диаметр окружности вершин зубьев
мм,
диаметр окружности впадин
мм.
Для колеса без смещения:
диаметр окружности вершин зубьев
мм,
диаметр окружности впадин
мм.