14 Закон распределения вероятностей Пуассона. Определение, числовые характеристики, связь с биномиальным распределением.
Рассмотрим
дискретную случайную величину Х,
принимающую только целые неотрицательные
значения (0, 1, 2,…, т,…), последовательность
которых не ограничена. Такая случайная
величина называется распределенной по
закону Пуассона, если вероятность
того, что она примет значение т,
выражается формулой:
где а – некоторая положительная
величина, называемая параметром
закона Пуассона.
Покажем, что сумма всех вероятностей равна 1:
(использовано разложение в ряд Тейлора функции ех).
Рассмотрим типичную задачу, приводящую к распределению Пуассона. Пусть на оси абсцисс случайным образом распределяются точки, причем их распределение удовлет-воряет следующим условиям:
вероятность попадания некоторого количества точек на отрезок длины l зависит только от длины отрезка и не зависит от его расположения на оси ( то есть точки распределены с одинаковой средней плотностью);
точки распределяются независимо друг от друга ( вероятность попадания какого-либо числа точек на данный отрезок не зависит от количества точек, попавший на любой другой отрезок);
практическая невозможность совпадения двух или более точек.
Тогда случайная величина Х – число точек, попадающих на отрезок длины l – распре-делена по закону Пуассона, где а – среднее число точек, приходящееся на отрезок длины l.
Замечание. В лекции 3 говорилось о том, что формула Пуассона выражает биномиальное распределение при большом числе опытов и малой вероятности события. Поэтому закон Пуассона часто называют законом редких явлений.
15 Случайная величина непрерывного типа. Плотность распределения вероятностей скалярной случайной величины. Определение, свойства, механическая интерпретация.
Определение 4.3. Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток.
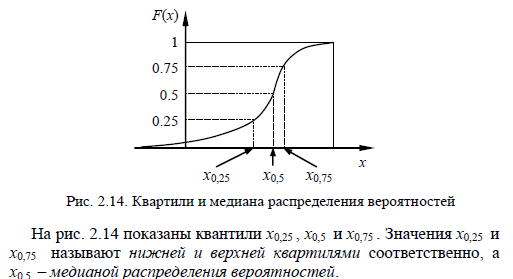
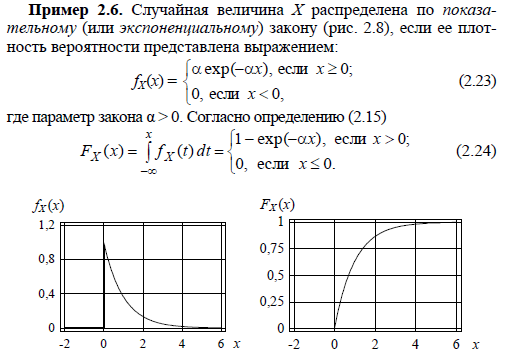
16 Описательные статистики распределений вероятностей: квантили, квартили, процентили, мода, медиана. Иллюстрация на примере правостороннего экспоненциального распределения.
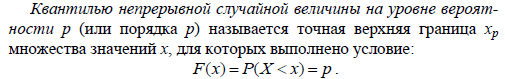
17 Векторные случайные величины. Функция распределения вероятностей случайного вектора. Определение и свойства. Вероятность попадания случайного вектора в прямоугольный параллелепипед с ребрами, параллельными осям координат.
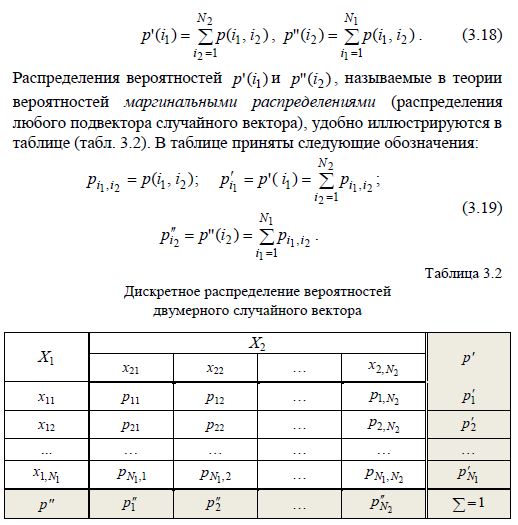
18 Случайный вектор дискретного типа. Табличное описание возможных значений случайного вектора для двумерного случая. Система обозначений. Функция распределения вероятностей, свойства.
19 Плотность распределения вероятностей случайного вектора непрерывного типа. Определение, свойства, механическая интерпретация. Вероятность попадания случайного вектора в окрестность заданной точки, в произвольную область с использованием плотности распределения вероятностей.
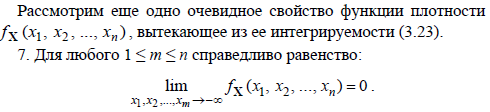
20 Независимость компонентов случайного вектора. Определение для распределений непрерывного и дискретного типов. Условные случайные величины и распределения вероятностей.
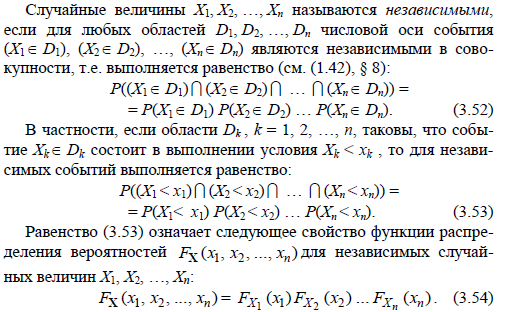
21 Числовые характеристики случайного вектора. Смешанные начальные и центральные моменты для случайных величин непрерывного и дискретного типов. Математическое ожидание случайного вектора, нормирование случайного вектора, ковариационная и корреляционная матрицы.