18 Вопрос.

Две прямые в пространстве могут пересекаться, быть параллельными и скрещиваться. Если две прямые пересекаются или параллельны, то они лежат в одной плоскости. Пусть две прямые заданы каноническими уравнениями:

Где, , точки принадлежащие прямым. Очевидно, чтобы прямые лежали в одной плоскости необходимо и достаточно чтобы векторы , и были компланарны, то есть их смешанное произведение равно нулю:

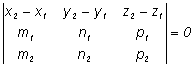- условие принадлежности двух прямых одной плоскости.

19 Вопрос

Введем в трехмерном пространстве прямоугольную систему координат Oxyz. Теперь каждой прямой соответствуют уравнения прямой некоторого вида, каждой плоскости отвечает уравнение плоскости. а каждой точке соответствует упорядоченная тройка чисел – координаты точки. Дальнейшее изложение подразумевает знание всех видов уравнений прямой в пространстве и всех видов уравнения плоскости, а также умение переходить от одного вида уравнений к другому виду. Но не пугайтесь, по тексту мы будем приводить ссылки на необходимую теорию.

20 Вопрос

Окружностью называется геометрическое место точек, равноудаленных от точки, называемой центром окружности (рис. 6).

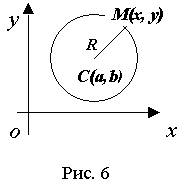
Пусть центр окружности находится в точке С(а, b). Т.к. окружность есть множество точек М(х, у), находящихся на расстоянии R (радиус окружности) от центра С(а, b), то , то есть

Уравнение (35) и есть каноническое уравнение окружности с центром в точке С(а, b) и радиусом R.

Эллипс есть геометрическое место точек, сумма расстояний от которых до двух фиксированных точек, называемых фокусами, есть величина постоянная (большая, чем расстояние между фокусами).

Внешний вид уравнения какого-либо геометрического места точек зависит от взаимного расположения этого множества точек и декартовой системы координат.

Выберем прямоугольную систему декартовых координат так, чтобы ось абсцисс проходила через оба фокуса F₁ и F₂, начало координат находится в середине отрезка F₁F₂ (рис. 7). Если обозначить расстояние между фокусами F₁ и F₂ через 2с, тогда координаты фокусов будут соответственно (-с, 0) и (с, 0).

Пусть М(х, у) - текущая точка эллипса (рис. 7).

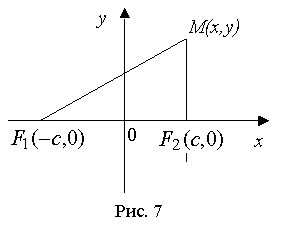
Обозначим сумму расстояний F1M и F2M через 2а (a > c по правилу треугольника), т.е. , или

Уравнение (36) и есть уравнение эллипса. Приведем его к более простой для исследований форме:

Поскольку a > c, то можно обозначить

тогда получаем

Окончательно получим (при выбранной системе координат) уравнение

Уравнение (38) называют каноническим уравнением эллипса.

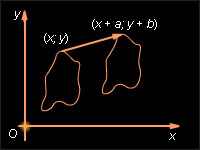
Введем на плоскости систему координат O, X, Y. Преобразование фигуры F, при котором произвольная ее точка M (x; y) переходит в точку   где a и b – одни и те же для всех точек (x; y), называется параллельным переносом. Параллельный перенос задается формулами   (*) которые выражают координаты образа  через координаты прообраза M при параллельном переносе.

Рисунок 12.3.1. Парралельный перенос

Следствие 12.2. 

• При a = b = 0 параллельный перенос совпадает с тождественным преобразованием. При этом каждая точка плоскости – неподвижная точка преобразования;

• При a² + b² > 0 параллельный перенос не имеет неподвижных точек.