4. Прямонаправленные сети. Обучение без учителя
Обучение без учителя (несупервизорное) предполагает, что нейросеть самостоятельно обрабатывает входную информацию с целью аппроксимации скрытых в ней зависимостей или классификации образов. При этом предполагается наличие некоторой целевой установки, определяющей действия сети при обработке входной информации. Обычно сеть, работающая без учителя, может сжимать информацию, кластеризовать ее, выделять некоторые признаки, формировать систему классов образов, содержащихся во входной информации.
В данной главе рассматриваются методы обучения нейросетей без учителя и типовые модели самообучающихся сетей. Подробно рассмотрены прямонаправленные нейросети (FFNN) с автоматической генерацией примеров, конкурентные сети типа карт Кохонена, аппроксимирующие сети с радиальными базисными функциями и сети для анализа главных компонент.
4.2Обучение без учителя
При
обучении без учителя НС
типа
FFNN
самостоятельно формируют выходы в
результате обработки информации и в
результате адаптируются к поступающей
на вход информации. При этом в процессе
самообучения НС предполагается
минимизация некоторого функционала.
Исходная информация поступает в сеть
в виде набора входных векторов
.
Важно выделить имеющуюся в ней
закономерность, отличающуюся от входного
шума. НС находит компактное описание
избыточных данных (обобщает их). Сжатие
данных и уменьшение степени их избыточности
может облегчить последующую работу с
ними и выделить существующие признаки.
Поэтому самообучающиеся НС используют
именно для предобработки "сырых"
данных.
Практически такие сети кодируют входную
информацию компактным при заданных
ограничениях кодом.
Длина
описания данных приблизительно равна
разности b,
определяющей возможное разнообразие
принимаемых ими значений, и размерности
d,
т.е. числу компонент
Соответственно различают два предельных
типа кодирования (рис.4.1а,б):
понижение d с минимальной потерей информации (анализ главных компонент данных или выделение набора независимых признаков);
уменьшение b, т.е. разнообразия данных за счет выделения конечного набора прототипов и отнесение данных к одному из них (кластеризация данных, квантование непрерывной входной информации).
Нейрон
– индикатор.
В простейшем случае нейрон с одним
выходом и d
входами обучается не наборе d
–
мерных данных
является индикатором. Схема
нейрона-индикатора без нелинейной части
представлена
на рис.4.2.
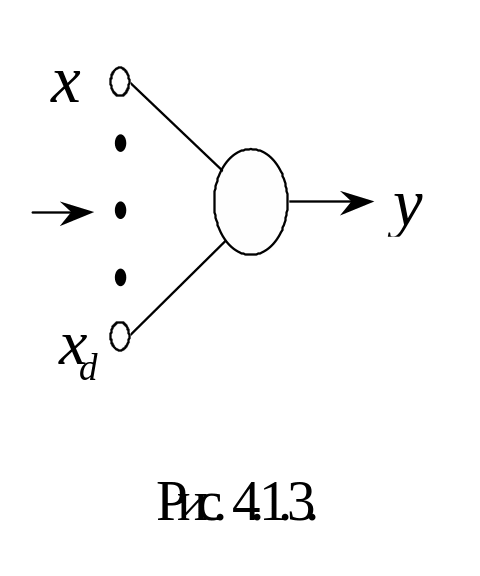
Выход такого нейрона определяется выражением:
.
(4.1)
Амплитуда выхода y может служить индикатором принадлежности входной информации к заданной группе примеров.
Правило Хебба. В 1949 году физиолог Хебб эмпирически установил следующее правило усиления весов в естественных НС:
Изменение весов нейрона при предъявлении ему p – го примера пропорционально его входам и выходу, т.е.
(векторный
вид) (4.2)
Если рассматривать обучение, как оптимизацию, то увидим, что нейрон, обучающийся по правилу Хебба, стремится увеличить амплитуду своего выхода:
,
(4.3)
где усреднение производится по обучающей выборке .
Вспомним, что обучение с учителем, напротив, базировалось на идее уменьшения ошибки воспроизведения примера (эталона). Если нет эталона, как в случае обучения без учителя, минимизация амплитуды y ведет к уменьшению чувствительности к входам. Напротив, максимизация y делает нейрон более чувствительным к различиям его входной информации, т.е. он становится полезным индикатором.
Но,
обучение по правилу Хебба в таком виде
на практике не применимо, т.к. приводит
к неограниченному возрастанию весов
.
Правило Ойя. Здесь по отношению к правилу Хебба добавляется член, препятствующий возрастанию весов:
.
(4.4)
При этом чувствительность выхода становится максимальной, но веса ограничиваются. Если приравнять среднее изменение весов к нулю и умножить правую часть на W, то получим:
,
т.е. веса расположены на гиперсфере:
(рис.4.3).
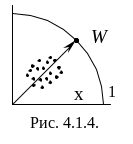
Это
правило, по существу, эквивалентно
-
правилу для ПТ, но обращенному назад –
от входов к выходам. Нейрон старается
воспроизвести значения своих входов
по заданному выходу, т.е. повышается
чувствительность выхода – индикатора
к многомерной входной информации
(оптимальное сжатие).
По другому это можно объяснить так: рассмотрим ПТ с одним линейным нейроном в скрытом слое и совпадающим числом входов и выходов, причем веса с одинаковыми индикаторами в слоях одинаковы. Будем учить ПТ воспроизводить в выходном слое значение своих выходов. При этом - правило второго слоя (и тем самым первого) принимает вид:
.
(4.5)
Это частный случай автоассоциативной сети (сети с узким "горлом"), соответствующей схеме, представленной на рис.4.4.
