6)Базис на прямой, на плоскости и в пространстве.

Базисом на прямой называется любой ненулевой вектор е на этой прямой (рис. 1.28). Этот вектор е называется базисным.

Пусть на прямой l задан базис вектор е не равен 0. Для любого вектора а , коллинеарного данной прямой, определено отношение ветор а:е=x, причем число x определяется однозначно. Таким образом, справедлива следующая теорема.

Любой вектор а коллинеарный прямой, может быть разложен по базису е на этой прямой, т.е. представлен в виде

Базисом на плоскости называются два неколлинеарных вектора е1 и е2 на этой плоскости, взятые в определённом порядке (рис. 1.29). Эти векторы е1 и е2 называются базисными.

Базис в пространстве.

Разложение вектора по базису.

Определение. Пусть  – произвольный вектор,  – произвольная система векторов. Если выполняется равенство

                   ,                       (1)

то говорят, что вектор  представлен в виде линейной комбинации данной системы векторов. Если данная система векторов  является базисом векторного пространства, то равенство (1) называется разложением вектора  по базису . Коэффициенты линейной комбинации  называются в этом случае координатами вектора  относительно базиса .

Теорема. (О разложении вектора по базису.)

Любой вектор векторного 5пространства можно разложить по его базису и притом единственным способом.

7)Скалярное произведение векторов.Определение,свойства.

Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на косинус угла между ними.

Скалярное произведение векторов , обозначается символом (порядок записи сомножителей безразличен, то есть ).

Если угол между векторами , обозначить через , то их скалярное произведение можно выразить формулой

(1)

СВОЙСТВА

5. Если векторы а и b (ненулевые) взаимно перпендикулярны, то их скалярное произведение равно нулю, т. е. если a b, B> ab=0. !?@0254;82> 8 >1@0B=>5 CB25@645=85: 5A;8 ab=0 и а 0 b, B> 0  b

Выражение скалярного произведения через координаты

Пусть заданы два вектора

Найдем скалярное произведение векторов, перемножая их как многочлены (что законно в силу свойств линейности скалярного произведения) и пользуясь таблицей скалярного произведения векторов i, j, k:

  

    т.е

Итак, скалярное произведение векторов равно сумме произведений их одноименных координат

8)Векторное произведение.Определение,свойства,геометрический смысл. Выражение в координатах.

9)Смешанное произведение. Определение, свойства, геометрический смысл, выражение через координаты.

10) Плоскость в пространстве. Нормальный вектор плоскости. Разлчные виды записи уравнения плоскости.

Нормаль — это прямая, ортогональная (перпендикулярная) касательному пространству (касательной прямой к кривой, касательной плоскости к поверхности и т. д.).

Вектор нормали к поверхности в данной точке — это единичный вектор, приложенный к данной точке и параллельный направлению нормали. Для каждой точки гладкой поверхности можно задать два нормальных вектора, отличающихся направлением. Если на поверхности можно задать непрерывное поле нормальных векторов, то говорят, что это поле задает ориентацию поверхности (то есть выделяет одну из сторон). Если этого сделать нельзя, поверхность называется неориентируемой.

Аналогично определяется вектор нормали к кривой в данной точке. Очевидно, что к кривой к данной точке можно приложить бесконечно много не параллельных векторов нормали (аналогично тому, как к поверхности можно приложить бесконечно много не параллельных касательных векторов). Среди них выбирают два, ортогональных друг к другу: вектор главной нормали и вектор бинормали.

11) Расстояние от точки до плоскости. Отклонение точки от плоскости.

12) Прямая в пространстве. Направляющий вектор прямой. Разлчные виды записи уравнения прямой в пространстве.

13) Прямая на плоскости . Различные виды записи уравнения прямой на плоскости.

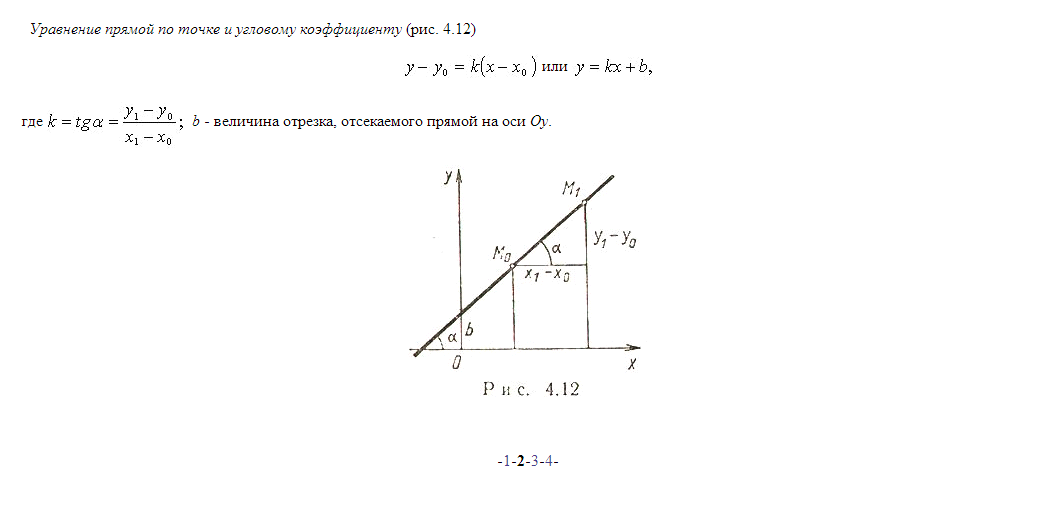
14) Кривые второго опрядка на плоскости. Эллипс. Гипербола. Парабола. Канонический вид и свойства.

15) Общее уравнение второго порядка, типы линий.

Типы линий:

16) Общее уравнение поверхности второго порядка. Основные уравнения в канонической форме.

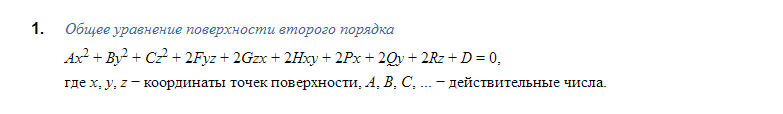
17) Арифметическое линейное пространство R^n. Примеры.

18) Линейная зависимость и независимость векторов в R^n, базис. Разложение вектора по базису.

19) Подпространство. Линеная оболочка системы векторов. Базис в подпространсвте.

хз чувак из книги брать надо.

20) Ранг системы векторов. Ранг матрицы. Приведение матрицы к ступенчатому виду.

21) Системы линейных алгебраических уравнений. Совместность системы. Теормера Кронекера - Капелли.

22) Свойства решений однородной и неоднородной систем уравнений.

23) Метод Гаусса для получения однородной и неоднородной систем уравнений.

ОДНОРОДНЫЕ СИСТЕМЫ.

Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например:

Пример решения:

Решить однородную систему линейных уравнений

Решение: чтобы решить  однородную систему необходимо записать матрицу системы и с помощью элементарных преобразований привести её к ступенчатому виду. Обратите внимание, что здесь отпадает необходимость записывать вертикальную черту и нулевой столбец свободных членов – ведь что ни делай с нулями, они так и останутся нулями:

(1) Ко второй строке прибавили первую строку, умноженную на –2. К третьей строке прибавили первую строку, умноженную на –3.

(2) К третьей строке прибавили вторую строку, умноженную на –1.

Делить третью строку на 3 не имеет особого смысла.

В результате элементарных преобразований получена эквивалентная однородная система , и, применяя обратный ход метода Гаусса, легко убедиться, что решение единственно.

Ответ:

НЕОДНОРОДНЫЕ СИСТЕМЫ

Пример 1

Решить систему линейных уравнений

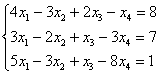
Что сразу бросается в глаза в этой системе? Количество уравнений – меньше, чем количество переменных. Если количество уравнений меньше, чем количество переменных, то сразу можно сказать, что система либо несовместна, либо имеет бесконечно много решений. И это осталось только выяснить

Начало решения совершенно обычное – запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:

(1) На левой верхней ступеньке нам нужно получить +1 или –1. Таких чисел в первом столбце нет, поэтому перестановка строк ничего не даст. Единицу придется организовать самостоятельно, и сделать это можно несколькими способами. Я поступил так: К первой строке прибавляем третью строку, умноженную на –1.

(2) Теперь получаем два нуля в первом столбце. Ко второй строке прибавляем первую строку, умноженную на 3. К третьей строке прибавляем первую строку, умноженную на 5.

(3) После выполненного преобразования всегда целесообразно посмотреть, а нельзя ли упростить полученные строки? Можно. Вторую строку делим на 2, заодно получая нужную –1 на второй ступеньке. Третью строку делим на –3.

(4) К третьей строке прибавляем вторую строку.

Наверное, все обратили внимание на нехорошую строку, которая получилась в результате элементарных преобразований: . Ясно, что так быть не может

Действительно, перепишем полученную матрицу    обратно в систему линейных уравнений:

Если в результате элементарных преобразований получена строка вида , где  – число, отличное от нуля, то система несовместна (не имеет решений).

Как записать концовку задания? Нарисуем белым мелом: «в результате элементарных преобразований получена строка вида , где » и дадим ответ: система не имеет решений (несовместна).