
- •Глава 1 Принципы управления системой элетроснабжения
- •1.2. Автоматизация управления системой электроснабжения
- •1.3 Информация в системах управления энергоснабжения
- •1.3.1 Общие понятия и определения об информации в системах управления электроснабжения
- •1.3.2. Количество сообщений и количество информации
- •1.3.3 Непрерывные и дискретные сигналы
- •1.3.2 Количество сообщений и количество информации
- •1.3.5 Модуляция
- •1.3.7. Кодирование
1.3.2 Количество сообщений и количество информации
Каждое событие или явление может иметь N различных состояний, поэтому сигнал, описывающий это событие, должен также иметь N состояний. Пусть требуется передавать на диспетчерский пункт информацию о состоянии четырех (п = 4) выключателей на контролируемом пункте. Каждый выключатель имеет два состояния (т - 2): «включен» и «отключен». Обозначим отключенное состояние выключателя «О», включенное — «1» и запишем все возможные сообщения о состоянии четырех выключателей.
Таблица 1.1
Варианты сообщений о состоянии выключателей
Номер сообщения |
Состояние выключателей |
Номер сообщения |
Состояние выключателей |
||||||
|
1 |
2 |
3 |
4 |
|
1 |
2 |
3 |
4 |
1 |
0 |
0 |
0 |
0 |
9 |
1 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
1 |
10 |
1 |
0 |
0 |
1 |
3 |
0 |
0 |
1 |
0 |
11 |
1 |
0 |
1 |
0 |
4 |
0 |
0 |
1 |
1 |
12 |
1 |
0 |
1 |
1 |
5 |
0 |
1 |
0 |
0 |
13 |
1 |
1 |
0 |
0 |
6 |
0 |
1 |
0 |
1 |
14 |
1 |
1 |
0 |
1 |
7 |
0 |
1 |
1 |
0 |
15 |
1 |
1 |
1 |
0 |
8 |
0 |
1 |
1 |
1 |
16 |
1 |
1 |
1 |
1 |
В табл. 1.1
перечислены все возможные сообщения о
состоянии четырех выключателей от
первого (все выключатели отключены) до
шестнадцатого (все выключатели включены).
Нетрудно убедиться, что между количеством
сообщений (N
= 16),
объектов (и = 4) и числом их состояний
(m
= 2)
существует зависимость 16 =
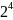 ,
которую можно записать (при произвольных
т и
п):
,
которую можно записать (при произвольных
т и
п):
N = mn. (1.1)
Число возможных сообщений является некоторой мерой информации. Однако пользоваться этой мерой неудобно, так как существует степенная зависимость между количеством сообщений и числом объектов, о которых необходимо передавать эти сообщения.
В системе телеуправления «Лисна-Ч» можно передавать сообщения о 126 объектах тяговых подстанций (п = 126). Количество сообщений, которое при этом может быть передано (N = 2126), определяется числом 1038 (число с 38 нулями).
Для измерения информации более удобна логарифмическая мера, которая позволяет получить линейную зависимость между количеством информации и числом объектов или числом элементов в сигнале, с помощью которого передается информация:
I = loga N = п loga m, (1.2)
где а — основание логарифма, которое может быть любым, но более удобно принять а — 2.
При т = 2 выражение (1.2) можно записать:
I = log2N = nlog22 = n. (1.3)
За единицу количества информации принимают информацию, содержащуюся в сообщении об объекте, имеющем два состояния. Сигнал, который описывает данное событие, состоит из одного элемента, имеющего также два состояния.
Единица количества информации носит название бит от английских слов binary digit (двоичная единица).
Таким образом, если двоичный сигнал состоит из одного элемента, он несет один бит информации, и с его помощью может быть передано только два сообщения типа «да-нет» (включено-отключено, 1-0).
Выражение (1.2) определяет наибольшее количество информации, которое может содержаться в сигнале данной структуры. Фактическое значение I может быть значительно меньше.
При передаче по каналам связи сигналов передаются определенные сообщения, в которых, кроме полезных, могут быть заранее известные или бессмысленные сведения. Истинное значение информации в сообщении определяется лишь полезными сведениями. Разница между истинным и наибольшим значением информации представляет собой избыточную информацию. Уменьшая избыточную информацию в реальных сообщениях, можно канал связи использовать более эффективно. Повседневно мы осуществляем сокращение избыточной информации, не думая о понятии «информация». Например, посылая поздравительную телеграммы, мы опускаем в тексте знаки препинания, предлоги, отдельные слова, имея в виду,что получателю и так будет понятен смысл сообщенияОднако в ряде случаев избыточная информация может быть полезной, помогая восстанавливать информацию при ее искажении помехой. Для повышения гарантии получения переданной информации без потерь нередко передают избыточную информацию. Так, например, в телеуправлении команда (включить, отключить) передается два раза, полное совпадение двух кодовых серий гарантирует отсутствие искажений команды.
Непрерывные и дискретные сигналы
Сигналы, как и сообщения, могут быть непрерывными и дискретными. параметры. Непрерывные сигналы используются в некоторых системах телеизмерения, а дискретные — в устройствах телеуправления и Непрерывные сигналы могут отличаться друг от друга на ничтожно малую величину, дискретные — имеют резко выраженные отличительные телесигнализации.
Типичным примером дискретных сообщений и сигналов является передача информации о состоянии выключателей на подстанции. Сигнал при этом состоит из импульсов, параметры которых, соответствующие включенному состоянию выключателей, существенно отличаются от параметров импульсов, несущих информацию об их отключенном состоянии. Промежуточных значений между этими двумя крайними сигнал, как и само состояние выключателей, не имеет: невозможно представить, что выключатель включен или отключен частично.
Передача дискретных сигналов имеет ряд преимуществ перед передачей непрерывных. Чтобы передать непрерывное сообщение, представленное непрерывной функцией времени X(t), ее разбивают на ряд дискретных значений. Замену непрерывного сообщения дискретным называют квантованием (дискретизацией). Квантование сигнала осуществляют либо по амплитуде, либо по времени. Замена непрерывного сигнала дискретным приводит к дополнительной погрешности. Однако это несущественно, если она невелика по сравнению с погрешностями, вызванными другими причинами.
На
рис. 1.5 представлено квантование сигнала
по амплитуде. При этом
кривую X(t)
разбивают
на равные интервалы АХ
по вертикали.
Интервал
АХ
называют
шагом
квантования. При
заданном шаге квантования
число дискретных значений сигнала
(разрешенных уровней) в
пределах изменения функции X(t)
от
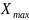 до
до
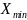 равно:
равно:
N= Если мгновенное значение функции попадает внутрь интервала, то оно заменяется ближайшим разрешенным. Переход с одного уровня на другой происходит в момент, когда значение функции находится в середине интервала квантования, так как именно в этот момент абсолютная погрешность квантования оказывается наибольшей.
Погрешность квантования определяется из выражения
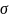 = +
100%
= +
100%
(1.5)
Из этого выражения видно, что с уменьшением ∆Х и увеличением N погрешность уменьшается.
При квантовании по времени кривую X(t) разбивают на равные интервалы по горизонтали и передают только те значения сигнала, которые совпадают с началом (или концом) каждого интервала. Следовательно, при квантовании по времени передача сигналов происходит в определенные фиксированные моменты времени.
Теоретически
скорость передачи информации по каналу
связи, определяющая пропускную способность
канала, может быть выражена формулой
С=∆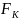 log2
log2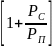 ,
бит/с где
∆FK
—
ширина полосы канала связи (полоса
частот, которую пропускает канал);
,
бит/с где
∆FK
—
ширина полосы канала связи (полоса
частот, которую пропускает канал);
отношение мощности сигнала к мощности помехи.
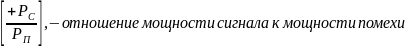 ,
,
Если в секунду передается С бит информации, то за время работы канала связи Тк можно передать количество информации
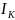 =∆
=∆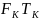 log2
,бит 17
log2
,бит 17
Мощность сигнала Рс не может быть больше мощности Рк, допустимой в канале. Приняв Рс = Рк, получим выражение, определяющее наибольшее количество информации в канале связи:
=∆ log2 ,бит
Обозначив
log2
=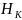 получим объем канала
получим объем канала
где динамический диапазон канала связи
По аналогии можно записать выражение объема сигнала:
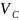 ==∆
==∆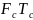 ,Hc,6m,
,Hc,6m,
(1-9)
(1.10)
е ∆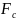 C
–ширина полосы частотного спектра
сигнала
C
–ширина полосы частотного спектра
сигнала
Те — длительность сигнала;
Нс — динамический диапазон сигнала.
Необходимым условием передачи сигнала по каналу связи является VK > Vc; к достаточным условиям относятся: ∆FK > ∆FC; Тк > Гс;
Нк>Нс.
. Сигналы и их спектры
Телемеханические сигналы, передаваемые по проводным линиям и радиоканалам, представляют собой электрическую величину, изменяющуюся во времени. В последние годы начинают широко применяться оптические сигналы, передаваемые по волоконно-оптическим кабелям.
Различают сигналы непериодические и периодические. Первые являются непериодической функцией времени, в простейшем случае —
это одиночные импульсы произвольной формы (рис. 1.6, а). Вторые являются периодической функцией времени и представляют собой бесконечную временную последовательность импульсов с одинаковой формой и периодом повторения Г (рис. 1.6, б).
Любая
периодическая функция времени F(t)
может
быть представлена
в виде суммы ряда синусоидальных
колебаний (ряда Фурье) с определенными
амплитудами Аi-,
начальными фазами
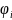 (-
и частотами.
Следовательно, любой периодический
сигнал можно представить в
виде ряда
(-
и частотами.
Следовательно, любой периодический
сигнал можно представить в
виде ряда
F(t)
= А0
+ А1
Sin(ωt +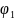 )
+ A2
sin(2 ωt +
)
+ A2
sin(2 ωt +
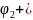 А3
Sin(ωt
+
А3
Sin(ωt
+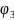 )+….
)+….
где — А0 постоянная составляющая (амплитуда нулевой гармоники); А1, А2, A3 — амплитуда соответственно гармоник 1, 2, 3;
ω = 2 nf— угловая частота первой гармоники;
f=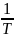
частота первой гармоники ГцГц;
Т— период повторения импульсов, с, который равен tH tn;
tи — время импульса.
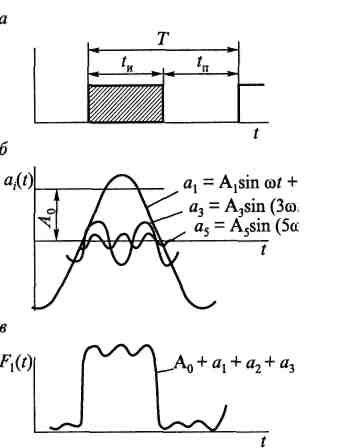
На рис. 1.7 представлен результат разложения прямоугольных импульсов (рис. 1.7, а) на гармонические составляющие (рис. 1.7, б). Амплитуды гармоник по мере возрастания частоты (номера) снижа-
w
F{t)
ются и обращаются
в нуль у тех, номера которых кратны
отношению
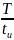 (при
tH
< tn
или
(при
tH
< tn
или
«Pi
?
+ <p3)
Л
+ф5)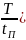 и
гармоники, номераt
и
и
гармоники, номераt
и
Рис. 1.7. Разложение прямоугольных импульсов на гармонические составляющие: а — последовательность прямоугольных импульсов; б — гармонические составляющие; в — синтезированная последовательность импульсов
которых кратны
2 (четные), обращаются в нуль. По этой
причине на рис. 1.7, б
отсутствуют
четные гармоники. На рис. 1.7, в
показана
последовательность, полученная в
результате
сложения нулевой А0,
первой
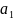 ,
третьей
,
третьей
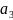 и пятой
а5
гармоник. Кривая наглядно показывает,
что чем больше гармоник суммируется,
тем ближе синтезированная последовательность
F1(t)
совпадает
с
исходной F(t)
(см.
рис. 1.7, а).
Чтобы
при передаче сигнала, состоящего из
последовательности прямоугольных
импульсов, не произошло искажений, нужно
передать по каналу весь бесконечный
ряд гармоник (1.11).
Практически осуществить это невозможно,
так как потребовался бы канал с
бесконечной полосой пропускания.
Обычно допустимы некоторые искажения
формы сигнала, что позволит ограничиться
передачей конечного числа гармонических
составляющих.
и пятой
а5
гармоник. Кривая наглядно показывает,
что чем больше гармоник суммируется,
тем ближе синтезированная последовательность
F1(t)
совпадает
с
исходной F(t)
(см.
рис. 1.7, а).
Чтобы
при передаче сигнала, состоящего из
последовательности прямоугольных
импульсов, не произошло искажений, нужно
передать по каналу весь бесконечный
ряд гармоник (1.11).
Практически осуществить это невозможно,
так как потребовался бы канал с
бесконечной полосой пропускания.
Обычно допустимы некоторые искажения
формы сигнала, что позволит ограничиться
передачей конечного числа гармонических
составляющих.
Амплитуды гармонических составляющих графически представляются в координатах Аk и f в виде отдельных спектральных линий (где к — номер гармоники). Совокупность амплитуд Аk. гармонических составляющих представляет собой спектр амплитуд, который называют линейчатым, так как он состоит из отдельных спектральных линий.
На рис. 1.8 приведены спектры амплитуд последовательностей прямоугольных импульсов одинаковой амплитуды и длительности,
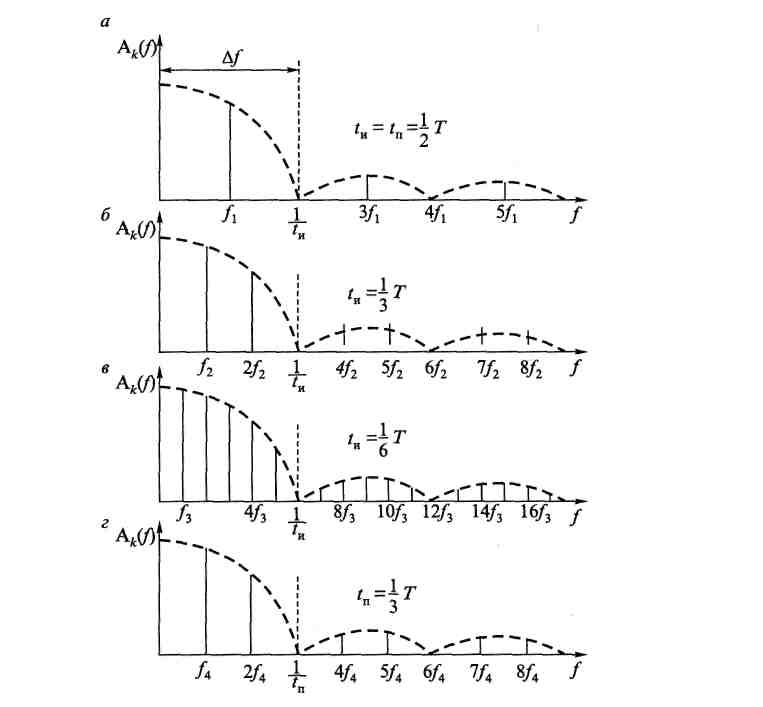
Рис. 1.8. Спектры амплитуд последовательностей импульсов одинаковой длительности с различными периодами:а при
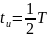 :
б —
при
:
б —
при
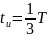 ;
в —
при
;
в —
при
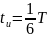 ;
г —
;
г —
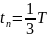
но
с различными периодами Т.
Амплитуды
гармоник с частотами кратными
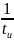 —
обращаются в нуль. Номер первой гармоники
с нулевой
амплитудой
—
(или
—
обращаются в нуль. Номер первой гармоники
с нулевой
амплитудой
—
(или
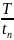 —), а ее частота
—), а ее частота
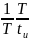 =
=
Если нет специальных оговорок относительно величины искажения импульсов при передаче, то достаточно ограничиться передачей только тех гармоник, частоты которых лежат между началом координат и частотой первой гармоники из числа тех, амплитуды которых равны нулю (первый «лепесток» спектра).
В этом случае ширина спектра сигнала или необходимая для передачи полоса канала связи определяется выражением
∆f=
при
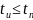 ил и ∆f=
ил и ∆f=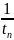 при
при
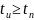
Из приведенных формул видно, что полоса пропускания канала связи обратно пропорциональна длительности наиболее короткого элемента сигнала (импульса или паузы).
Непериодические
сигналы можно рассматривать как
периодические с периодом повторения
равным бесконечности. Из
приведенных на рис. 1.8 спектров видно,
что при увеличении периода Т,
частотное
расстояние
между спектральными линиями уменьшается,
а количество линий
увеличивается. Нетрудно представить,
что при увеличении периода до
бесконечности, спектральные линии
сближаются настолько, что
сливаются между собой, а их число
увеличивается до бесконечности
на любом конечном интервале частот. В
этом случае нет необходимости говорить
об отдельных гармонических составляющих
сигнала,
и поэтому вводят понятие спектральной
плотности S(f)
как
функции
частоты. График спектральной плотности
одиночного прямоугольного
импульса (рис. 1.9, а,
б) показывает,
что огибающая кривая
обращается в нуль при частотах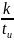 — , где к
= 1, 2, 3 и
т.д.
— , где к
= 1, 2, 3 и
т.д.
Для передачи сигнала используют предельно малую ширину спектра, но такую, чтобы в ней была сосредоточена основная энергия сигнала. Из рис. 1.9, б видно, что наибольшая энергия сигнала сосредоточена в пределах первого «лепестка» спектра. Отсюда необходимая для передачи полоса канала связи определяется выражением
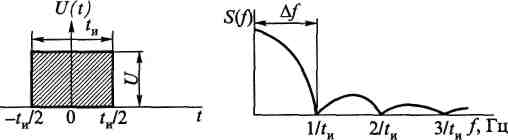
Рис. 1.9. График спектральной плотности одиночного прямоугольного импульса: а — прямоугольный импульс; б — график спектральной плотности
∆f =
которое совпадает с выражением (1.12) для последовательности прямоугольных импульсов.
