1.3.1. Дифференциальное уравнение динамики объекта
Выведем дифференциальное уравнение переходного процесса, справедливое для основных одноемкостных объектов регулирования. Физические процессы, протекающие в объектах регулирования, могут быть описаны следующим обобщенным уравнением:
(4)
где t — время;
, q и B — обобщенные величины.
Величина q является регулируемой, величина B характеризует результирующее энергетическое воздействие, изменяемое при помощи регулирующего органа, а величина L характеризует собственные свойства объекта. В общем случае параметр B равен разности притока (поступающей) Qпр энергии и расхода (потребляемой) Qр энергии, т.е. B = Qпр - Qр. При установившемся режиме B = 0
Допустим, что в некоторый момент времени произошло мгновенное небольшое изменение притока и расхода энергии на величину Q, т.е.
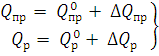(5)
где
и 
— начальные значения притока и расхода
энергии.
В результате изменения притока и расхода энергии величина регулируемого параметра также изменится на величину q.
Запишем уравнение (4) в приращениях для этого возмущенного состояния:
.
(6)
Будем считать, что приток энергии Qпр зависит от положения регулирующего органа l и значения регулируемой величины q, а расход энергии Qр — только от значения регулируемой величины q, т.е. что
.
(7)
В общем случае указанные зависимости (7) являются нелинейными, в результате чего аналитическое исследование процесса сильно усложняется, а в некоторых случаях вообще не представляется возможным, т.е. решение уравнений динамики не может быть представлено в общем виде. Однако, учитывая, что в течение переходного процесса происходят малые отклонения регулируемых величин от их установившихся значений, действительные нелинейные зависимости в большинстве случаев можно заменить линейными. Такая операция замены нелинейных зависимостей линейными при малых отклонениях величин носит название линеаризация. Для линеаризации этих функций разложим их в ряд Тейлора и учтем только первые члены разложений:
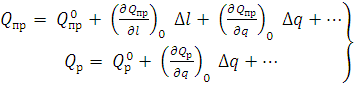(8)
Подставляя выражение (8) в уравнение (5), получим:
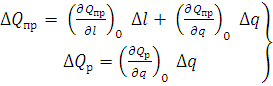(9)
В выражениях (8) и (9) индекс нуль, стоящий у скобки, указывает на то, что значения производных определяются при исходном установившемся режиме, и, следовательно, эти значения являются постоянными величинами.
Подставим выражение (9) в уравнение (6):
.
Перенесем члены уравнения, содержащие q, в левую сторону:
.
Поделив все члены уравнения на выражение в квадратной скобке, получим:
.
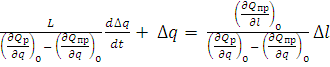(10)
Введя обозначения:
;
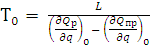(11)
;
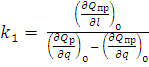(12)
х = l — приращение координаты регулирующего органа;
y = q — приращение регулируемого параметра,
получим уравнение одноемкостного объекта в следующем виде:
.
(13)
Величина Т0 называется постоянной времени объекта, а k1 — коэффициентом усиления.
Операторная форма записи дифференциальных уравнений. Если в дифференциальном уравнении заменить знак производной символом p, т.е. обозначить:
,
(14)
то производные при этом можно представить как
.
(15)
Для операции интегрирования действительны соответственно обратные обозначения:
и т.д. (16)
В этом случае произвольное дифференциальное уравнение 3-го порядка, правая часть которого имеет также дифференциальную форму,
,
(17)
в операторной форме может быть представлено так:
.
(18)
Полином
называют собственным
оператором,
а полином 
– оператором
воздействия.
В общем виде уравнение (18) можно представить в такой форме:
,
(19)
где d(p) — собственный оператор;
k(p) — оператор воздействия.
Если собственный оператор приравнять к нулю, получается характеристическое уравнение.
Полученное ранее дифференциальное уравнение объекта в операторной форме запишется следующим образом:
.
(20)