Глава 3

УСТОЙЧИВОСТЬ И КАЧЕСТВО СИСТЕМ

АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ

3.1. Определение устойчивости

Основным назначением САР является поддержание регулируемой величины на заданном уровне при наличии воздействия на систему внешних возмущений. Поэтому систему автоматического регулирования называют устойчивой, если, будучи выведенной из состояния равновесия и предоставленной самой себе, она с течением времени будет стремиться вернуться к равновесному состоянию.

Устойчивость системы определяется характером свободного движения, которое, как известно, описывается однородным дифференциальным уравнением (без правой части). Поэтому форма правой части уравнения, описывающего динамику системы, не оказывает влияния на устойчивость.

В общем случае свободное движение системы можно описать однородным дифференциальным уравнением вида:

, (72)

где у — регулируемая величина;

а₀, а₁ ... а_п — постоянные коэффициенты, определяемые параметрами системы.

Согласно определению система будет устойчивой, если

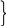
(73)

Решение уравнения (72) можно представить в следующем виде:

, (74)

где С_i — постоянные интегрирования, определяемые из начальных условий,

p_i — корни характеристического уравнения (75), соответствующего дифференциальному уравнению (72):

. (75)

Условие (73) может быть выполнено в том случае, если все составляющие решения (74) с течением времени будут стремиться к нулю. Так как все коэффициенты С_i — величины постоянные, то характер каждой составляющей зависит только от p_i.

Если p_i будет положительной вещественной величиной, то будет с течением времени увеличиваться до бесконечности. Если p_i будет отрицательной вещественной величиной, то будет с течением времени стремиться к нулю. В том случае, если — комплексная величина, то

—

переходный процесс колебательный, амплитуда А которого будет возрастать или убывать в зависимости от знака вещественной части комплексного корня. При этом, если вещественная часть комплексного корня будет положительной величиной, то переходный процесс будет колебательным с нарастающим значением амплитуды колебаний, т. е. будет расходящимся; если же вещественная часть комплексно-сопряженного корня будет отрицательной величиной, амплитуда колебаний с течением времени будет стремиться к нулю.

Так как вещественные корни представляют собой частный случай комплексных (при β=0), то на основании приведенных соображений вытекает следующее условие устойчивости линейных систем. Для того чтобы линейная САР была устойчива, необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения САР были отрицательными.

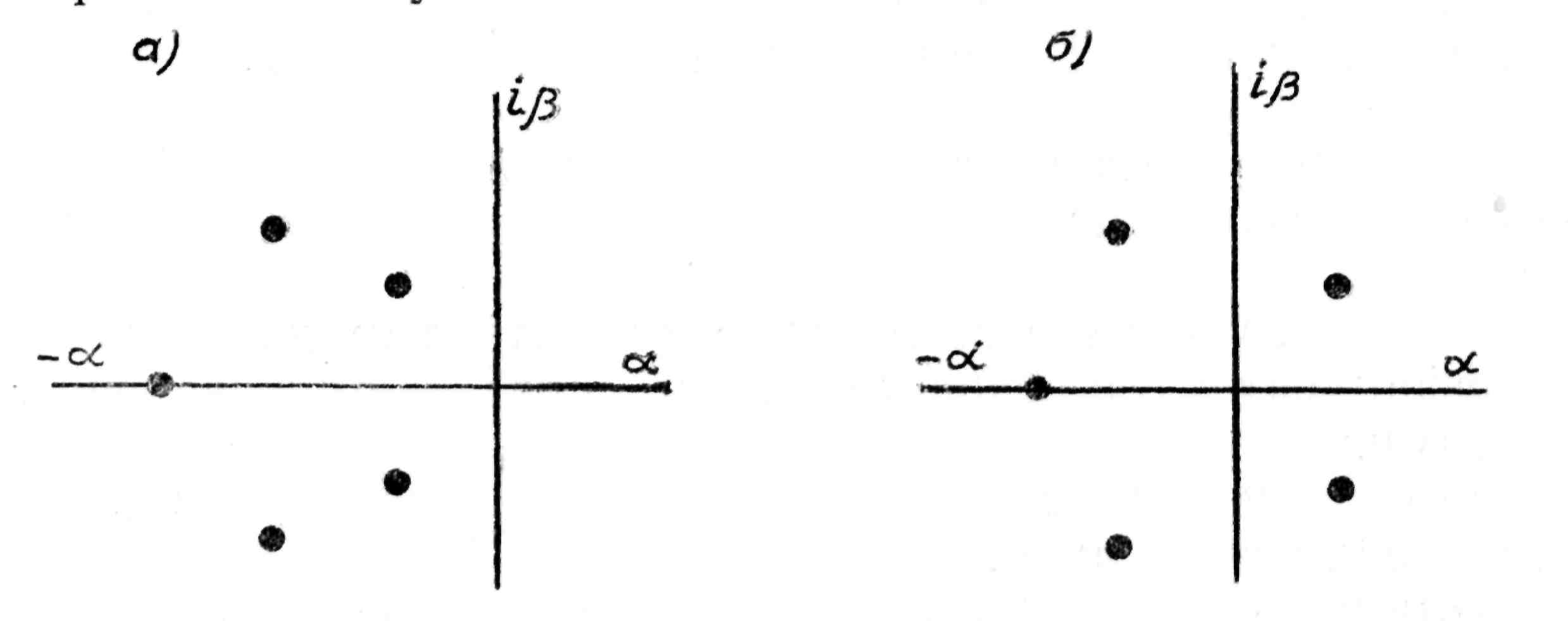
Рис. 41. Распределение корней характеристического уравнения

на комплексной плоскости:

а — устойчивая система; б — неустойчивая система

Если корни характеристического уравнения расположить на комплексной плоскости, то для устойчивости системы необходимо и достаточно, чтобы все корни лежали слева от мнимой оси. Если пара комплексных корней лежит на мнимой оси, а остальные — слева от нее, то система находится на границе устойчивости. На рис. 41 показано распределение корней характеристического уравнения 5-го порядка. Таким образом, исследование устойчивости сводится к определению знаков вещественной части корней характеристического уравнения.