2.3. Типовые динамические звенья
Несмотря на то, что звенья, входящие в состав различных САР, отличаются во многих случаях друг от друга как по конструктивному выполнению, так и по функциональному назначению, представляется возможным свести их к сравнительно небольшой группе звеньев, отличающихся одинаковыми динамическими свойствами. При такой классификации по динамическим свойствам звенья, переходные процессы в которых описываются одинаковыми уравнениями, относят к одному типу динамического эвена.
В теории автоматического регулирования принято различать следующие основные динамические звенья: пропорциональное или безынерционное, апериодическое или инерционное, колебательное, дифференцирующее, интегрирующее, с чистым запаздыванием.
Динамические свойства пропорционального или безынерционного звена описываются уравнением вида:
,
(44)
а переходный процесс имеет вид, изображенный на рис. 27.
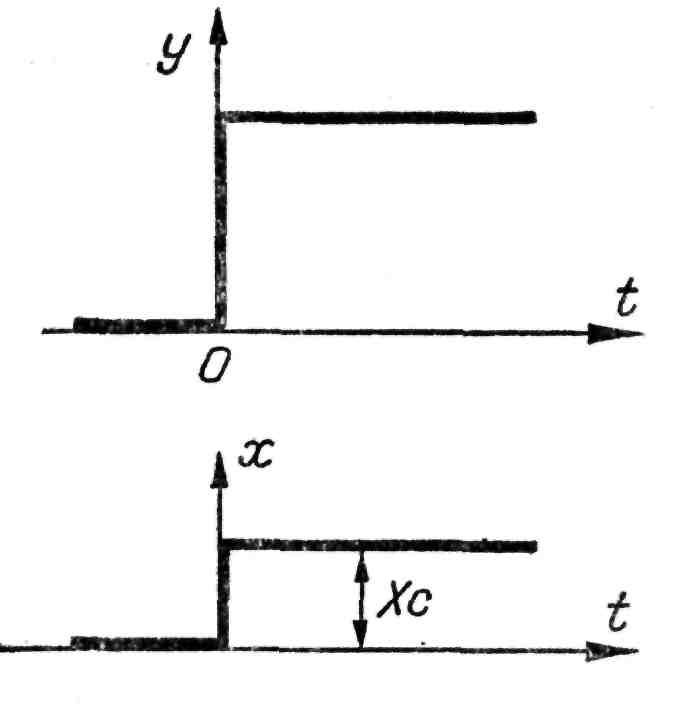
Рис. 27. Переходный процесс безынерционного звена
Передаточная и частотная функции этого звена описываются следующими выражениями:
;
(45)
.
(46)
Динамика апериодического звена описывается уравнением
.
(47)
При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (см. рис. 22):
.
(48)
Передаточная и частотная функции этого звена имеют следующие выражения:
;
(49)
.
Амплитудно-фазовая характеристика этого звена представлена на рис. 28.
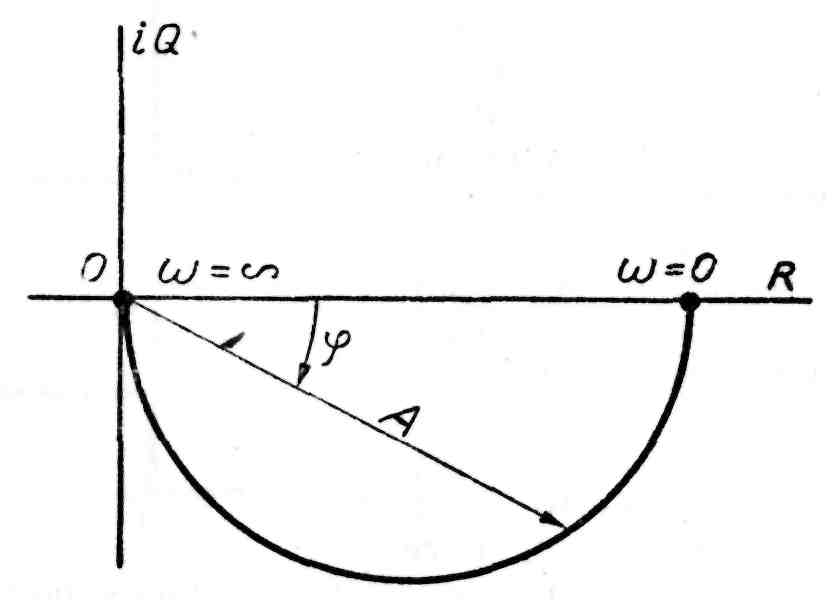
Рис. 28. Амплитудно-фазовая характеристика
апериодического звена 1-го порядка
Динамика колебательного звена описывается уравнением
.
(50)
При ступенчатом возмущении и нулевых начальных условиях переходная функция имеет вид (рис. 29):
,
(51)
где
— постоянная
времени огибающей экспоненты;
.
Передаточная и частотная функции колебательного звена будут иметь выражения:
;
(52)
.
(53)
Рис. 29. График переходного процесса колебательного звена
Амплитудно-фазовая характеристика колебательного звена представлена на рис. 26.
В
том случае, если в уравнении будет иметь
место неравенство 
,
то
звено превращается в апериодическое
2-го порядка с переходной функцией
,
(54)
где
;
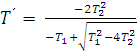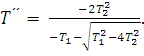
Переходный процесс в этом случае будет иметь вид, представленный на рис. 30.
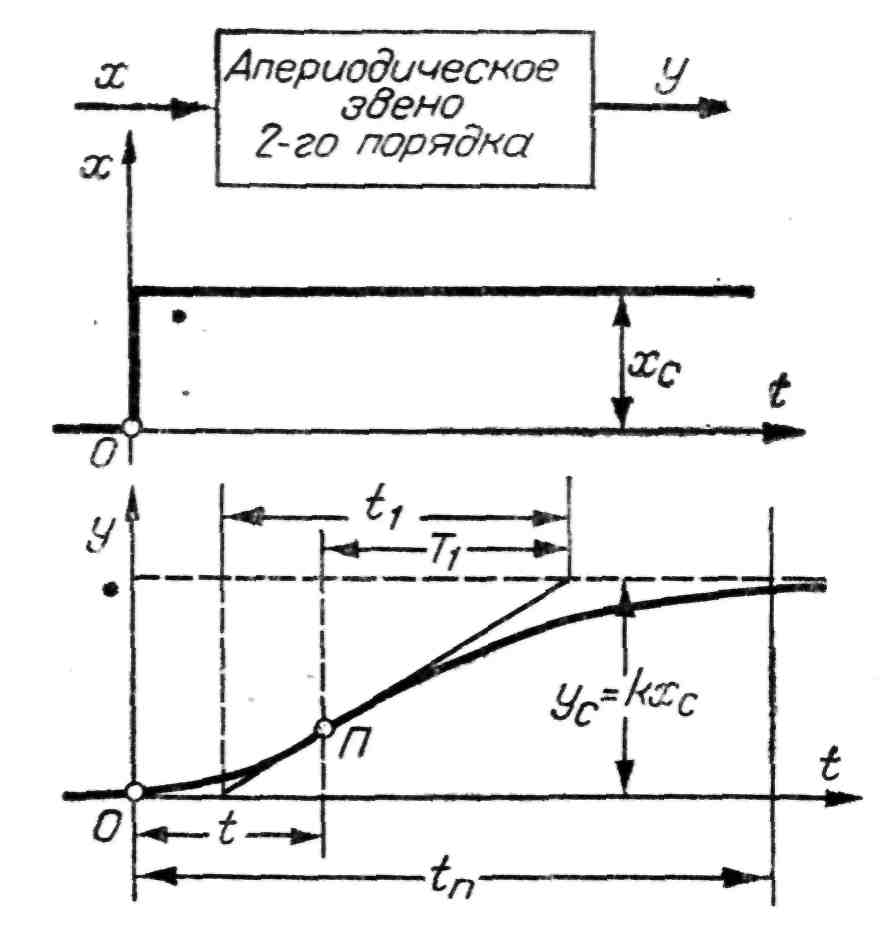
Рис. 30. График переходного процесса
апериодического звена 2-го порядка
Идеальным дифференцирующим называется звено, динамика которого описывается уравнением вида:
.
(55)
График переходной функции этого звена показан на рис. 31 и представляет собой мгновенный импульс, который возникает только в момент подачи ступенчатого входного возмущения. Передаточная и частотная функции идеального дифференцирующего звена:
;
.
(56)
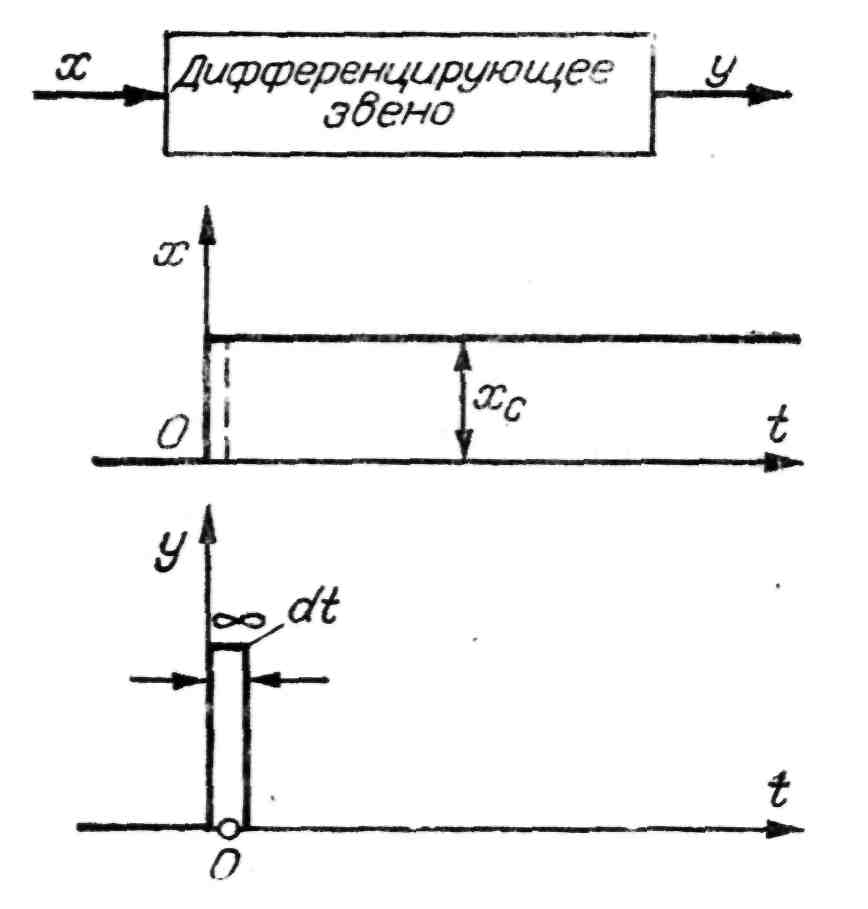
Рис. 31. Переходный процесс идеального
дифференцирующего звена
Большинство реальных систем обладают определенной инерционностью. Динамика инерционного дифференцирующего звена может быть описана уравнением вида:
.
(57)
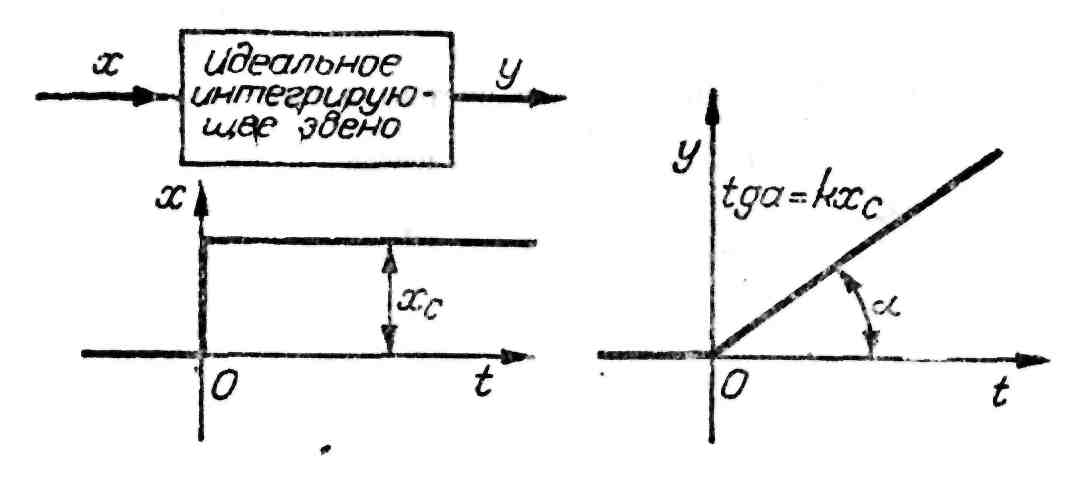
Рис. 32. Переходный процесс идеального интегрирующего звена
Динамика идеального интегрирующего звена описывается уравнением вида
(58)
или
,
(59)
а в операторной форме
.
(60)
Из уравнения (58) следует, что если на вход интегрирующего звена подать ступенчатое возмущение, то выходная величина будет со временем беспрерывно увеличиваться.
Графики переходного процесса такого звена показаны на рис. 32. Передаточная и частотная функции определяются по уравнениям:
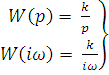(61)
Уравнение динамики реального интегрирующего звена будет:
.
(62)
Дифференцируя обе части уравнения, можно получить другое выражение:
.
(63)
В ряде случаев изменение выходной величины начинается не одновременно с изменением входной, а спустя некоторый промежуток времени, называемый запаздыванием.
Различают звенья с чистым или транспортным запаздыванием, примером которого может служить ленточный питатель (рис. 33). Если входной координатой считать положение шибера на питающем бункере 1 (х), а выходной координатой — количество материала, поступающего в бункер (Q), то переходная характеристика этого звена может быть описана уравнением
,
(64)
где t — время;
— время чистого или транспортного
запаздывания.
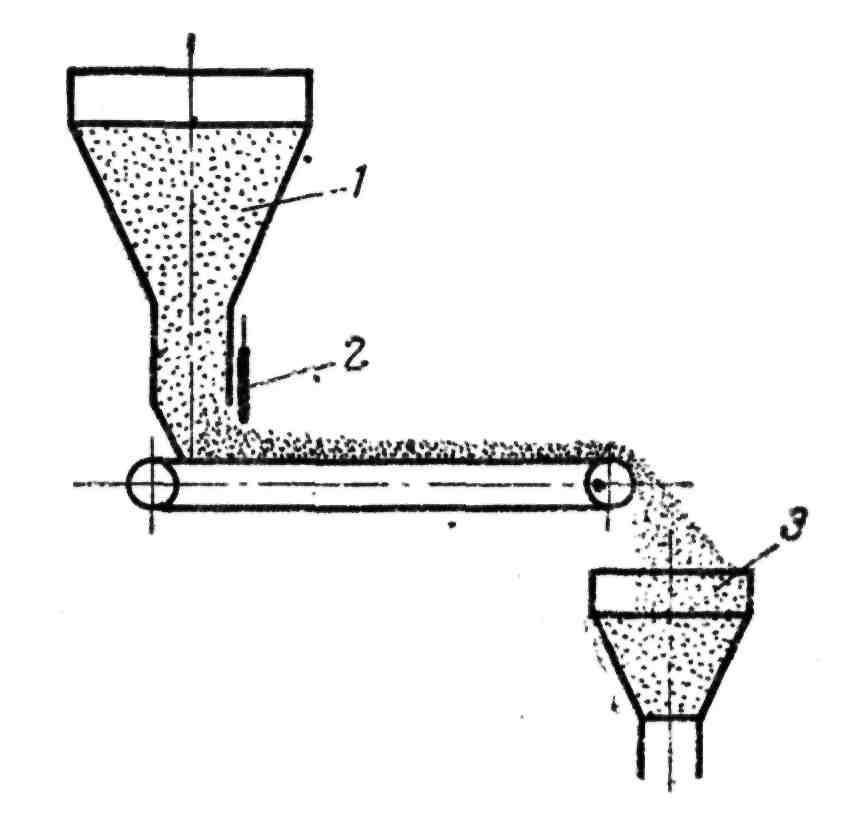
Рис. 33. Схема звена с чистым запаздыванием:
1, 3 – бункера; 2 - шибер
В общем случае любое звено с запаздыванием можно рассматривать состоящим из обыкновенного звена без запаздывания и идеального звена с чистым запаздыванием. Передаточная функция звена с запаздыванием в общем случае будет иметь выражение
,
(65)
где W0(p) — передаточная функция звена без запаздывания.
Рис. 34. Переходные процессы:
а – идеальное звено с чистым запаздыванием;
б – инерционное звено с чистым запаздыванием
Переходные процессы для идеального звена с запаздыванием и для инерционного звена при наличии чистого запаздывания приведены на рис. 34.