3.4. Функции из отдельных кусков
piecewise(cond_1,f,cond_2,f..2…cond_n,f_n,f_otherwise)
где f – i-е выражение
cond – i-е логическое выражение
f_otherwise – определяемые опционально выражения
В зависимости от того или иного условия эта функция позволяет формировать ту или иную аналитическую зависимость.
Созданная с помощью piecewise зависимость может участвовать в различных преобразованиях (например она дифференцируется и можно построить график ее производной). При этом каждая часть функции обрабатывается отдельно.
Пример:
> f:=х-> piecewise(x^2>4,x^2,-2*x^2);
> f(х);
> plot (f(x),x=-5..5,color=blue);
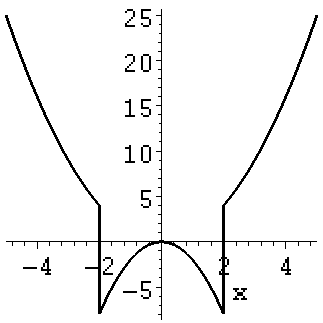
> plot (diff(f(x),x),x=-5..5,color=black);
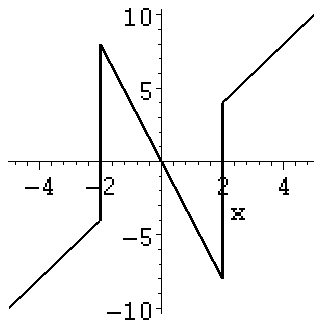
4. Действия с рядами
4.1. Вычисление сумм рядов
Вычисление суммы членов некоторой последовательности f(k) при изменении целочисленного индекса k от значения m до значения n с шагом +1, т.е выражение:
Функции для вычисления этой суммы :
sum(f,k) sum(f,k=m..n) sum(f,k=alpha)
Sum(f,k) Sum (f,k=m..n) Sum(f,k=alpha)
где f – функция, задающая члены суммируемого ряда;
k – индекс суммирования;
m, n – целочисленные пределы изменения k;
alpha – RootOF-выражение.
Если n= ∞, используется константа infinity.
Пример:
> Sum (k^2,k=1..4);
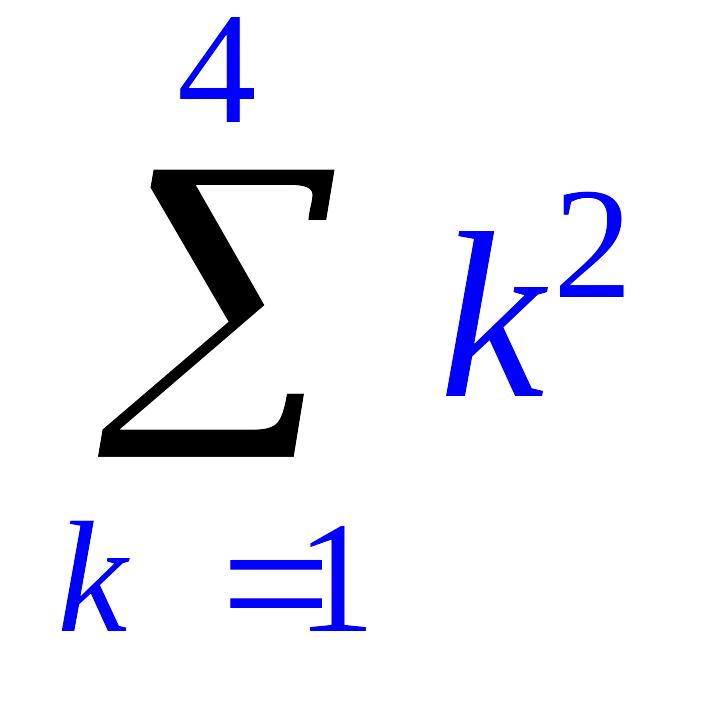
> sum (k^2,k=1..4);
> sum (a[k],k=1..4);
4.2. Вычисление произведений
Выражение:
Функции:
рroduct – находит произведение
Product – инертная форма функции рroduct
product(f,k) рroduct(f,k=m..n) рroduct(f,k=alpha)
Product(f,k) Рroduct(f,k=m..n) Рroduct(f,k=alpha)
Пример:
> Product(k^2,k=1..4);
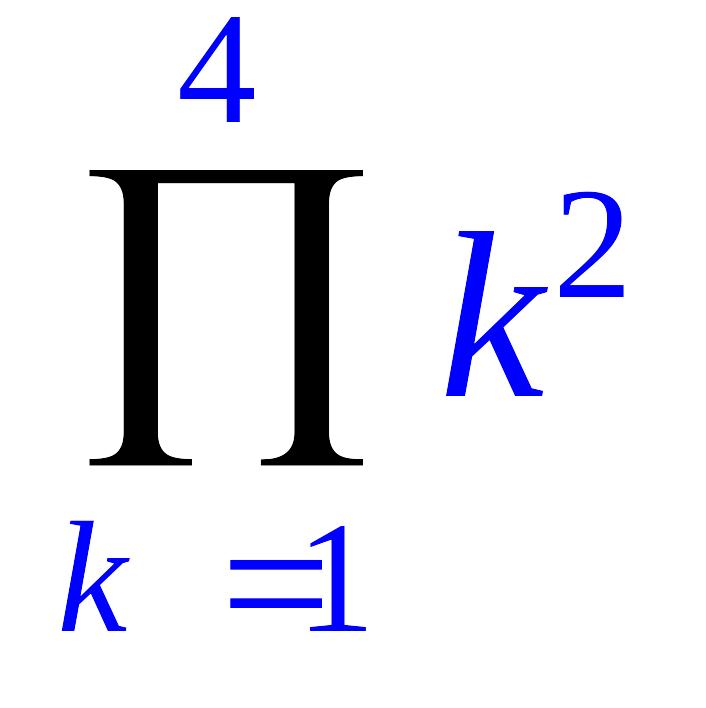
> product(k^2,k=1..4);
> product(a[k],k=1..4);
5. Вычисление корней полинома
Для вычисления многовариантных полиномов.
roots (p) roots (p,k)
roots (p,x) roots (p,x,k)
Функции вычисляют точные корни в рациональной или алгебраической области чисел. Корни возвращаются в виде [[r1,m1],…[rn,mn]].
где ri – корень полинома
mi – порядковый номер полинома.
Пример:
> roots(x^2-4,x);
> expand((x-1)*(x-2)*(x-3)*(x-4));
> roots (%,x);
Задание
1. Записать в математической форме и вычислить неопределенный интеграл функции f(х).
Вариант |
Функция |
Вариант |
Функция |
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
2. Записать в математической форме и вычислить определенный интеграл.
Вариант |
Функция |
Интервал |
Вариант |
Функция |
Интервал |
1 |
∫ x (1 – x) dx |
0 .. 1 |
16 |
∫ x2 sin 2x /(x2 + 1) |
-3 .. 3 |
2 |
∫ sin x / x dx |
π /2 .. π |
17 |
∫ x arctg x dx |
-1 .. 1 |
3 |
∫ x3
|
1 .. 3 |
18 |
∫ ex cos x dx |
0 .. π/2 |
4 |
∫ x / (1 + x4) dx |
0 .. 1 |
19 |
∫ dx / x2 + x |
1 .. 2 |
5 |
∫ e1/x/ x2 dx |
1 .. 2 |
20 |
∫ cos3x sin 2x dx |
0 .. 3 π |
6 |
∫ 5x ex dx |
0 .. 1 |
21 |
∫ esin x dx |
0 .. π/2 |
7 |
∫ sin2x / cos x dx |
0 .. π/6 |
22 |
∫ cos 5x cos x dx |
0 .. 2 π |
8 |
∫ 1 / (ex – 1) dx |
ln 2 .. 2 ln 2 |
23 |
∫ x3 dx |
1 .. 3 |
9 |
∫ cos 5x cos x dx |
0 .. 2 π |
24 |
∫ x (1 – x) dx |
0 .. 1 |
10 |
∫ cos3x sin 2x dx |
0 .. 3 π |
25 |
∫ sin x / x dx |
π /2 .. π |
11 |
∫ dx / x2 + x |
1 .. 2 |
26 |
∫ x / (1 + x4) dx |
0 .. 1 |
12 |
∫ ex cos x dx |
0 .. π/2 |
27 |
∫ 5x ex dx |
0 .. 1 |
13 |
∫ x arctg x dx |
-1 .. 1 |
28 |
∫ e1/x/ x2 dx |
1 .. 2 |
14 |
∫ x2 sin 2x /(x2 + 1) |
-3 .. 3 |
29 |
∫ sin2x / cos x dx |
0 .. π/6 |
15 |
∫ esin x dx |
0 .. π/2 |
30 |
∫ 1 / (ex – 1) dx |
ln 2 .. 2 ln 2 |
dx
3. Записать в математической форме и вычислить двойной интеграл:
а) с помощью команды int
б) с помощью пакета student
вариант |
|
вариант |
|
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
4. Записать в математической форме и вычислить тройной интеграл:
а) с помощью команды int
б) с помощью пакета student
Вариант |
|
Вариант |
|
1 |
|
16 |
|
2 |
|
17 |
|
3 |
|
18 |
|
4 |
|
19 |
|
5 |
|
20 |
|
6 |
|
21 |
|
7 |
|
22 |
|
8 |
|
23 |
|
9 |
|
24 |
|
10 |
|
25 |
|
11 |
|
26 |
|
12 |
|
27 |
|
13 |
|
28 |
|
14 |
|
29 |
|
15 |
|
30 |
|
5. Вычислить интеграл по частям
Вариант |
Интеграл |
u(x) |
Вариант |
Интеграл |
u(x) |
1 |
∫ arctg x dx |
u(x) = arctg x |
16 |
∫ x e-х dx |
u(x) = x |
2 |
∫ ln x dx |
u(x) = ln x |
17 |
∫ ln2 x / х dx |
u(x) = ln x |
3 |
∫ x sin x dx |
u(x) = x |
18 |
∫ x sin x / cos2 x dx |
u(x) = x |
4 |
∫ x2 ex dx |
u(x) = x2 |
19 |
∫ x2 ex dx |
u(x) = x2 |
5 |
∫ ex sin x dx |
u(x) = ex |
20 |
∫ sin |
u(x) = |
6 |
∫ |
u(x) = |
21 |
∫ arcsin x dx |
u(x) = arcsin x |
7 |
∫ 1 / (x2 + 4) |
u(x) = x |
22 |
∫ ex sin x dx |
u(x) = ex |
8 |
∫ x ln x dx |
u(x) = ln x |
23 |
∫ arctg x dx |
u(x) = arctg x |
9 |
∫ arcsin x dx |
u(x) = arcsin x |
24 |
∫
|
u(x) = x2 |
10 |
∫ (x + 1) ex dx |
u(x) = x + 1 |
25 |
∫ e2x cos x dx |
u(x) = e2x |
11 |
∫ x2 sin x dx |
u(x) = x2 |
26 |
∫ x e-х dx |
u(x) = x |
12 |
∫ x2 arctg x dx |
u(x) = arctg x |
27 |
∫ (x + 1) ex dx |
u(x) = x + 1 |
13 |
∫ dx |
u(x) = x2 |
28 |
∫ 1 / (x2 + 4) |
u(x) = x |
14 |
∫ e2x cos x dx |
u(x) = e2x |
29 |
∫ x sin x / cos2 x dx |
u(x) = x |
15 |
∫ sin dx |
u(x) = |
30 |
∫ ln2 x / х dx |
u(x) = ln x |
dx
dx
dx
6. Вычислить определенный интеграл функции f(х), используя подстановку t
вариант |
Функция |
Подстановка |
х1 |
х2 |
1 |
f(x) = (2х – 1)20 |
t = 2x – 1 |
0 |
1 |
2 |
f(x) = sin(3x + 1) |
t = 3x + 1 |
-1 |
2 |
3 |
f(x)
= x2 |
t = x3 + 5 |
1 |
2 |
4 |
f(x) = х / (x2 + 1) |
t = x2 + 1 |
-1 |
1 |
5 |
f(x)
= 1/(x |
t = |
2 |
3 |
6 |
f(x)
= sin
2x /
|
t = cos2 x |
π/2 |
π |
7 |
f(x) = (2 sin х + 3)2 cos x |
t = 2 sin х + 3 |
π/2 |
π |
8 |
f(x)
= x4
/
|
t = x5 |
0 |
1 |
9 |
f(x) = x / (x4 + 2x2 + 5) |
t = x2 + 1 |
1 |
2 |
10 |
f(x) = e2x / (e4x – 5) |
t = e2x |
0 |
1 |
11 |
f(x)
= e |
t = |
1 |
2 |
12 |
f(x) = sin(2 – 3x) |
t = 2 – 3x |
0 |
0,5 |
13 |
f(x) = х (x2 + 1)3/2 |
t = x2 + 1 |
1 |
3 |
14 |
f(x) = х / (x2 – 1) |
t = x2 – 1 |
1 |
3 |
15 |
f(x)
= x
/
|
t = x2 |
2 |
4 |
16 |
f(x) = sin 4x / (cos42x + 4) |
t = cos22x |
0 |
1 |
17 |
f(x)
= ex/2
/
|
t = ex/2 |
2 |
4 |
18 |
f(x) = х3 (1 – 2x4)3 |
t = 1 – 2x4 |
1 |
2 |
19 |
f(x) = x ch(5x2 + 3) |
t = 5x2 + 3 |
-1 |
0 |
20 |
f(x)
= х2
/
|
t = |
2 |
3 |
21 |
f(x)
= x3
/
|
t = x4 |
0 |
1 |
22 |
f(x) = e3x / (e6x – 5) |
t = e3x |
0 |
1 |
23 |
f(x) = sin(2x – 5) |
t = 2x – 5 |
-1 |
2 |
24 |
f(x) = х / (x3 + 3) |
t = x3 + 3 |
1 |
3 |
25 |
f(x) = (3х + 4)10 |
t = 3x + 4 |
0 |
0,2 |
26 |
f(x)
= ex
/
|
t = ex |
2 |
4 |
27 |
f(x) = х4 (2– 5x5)2 |
t = 2 – 5x5 |
1 |
2 |
28 |
f(x)
= e |
t = |
0 |
2 |
29 |
f(x) = cos(5 + 2x) |
t = 5 + 2x |
0 |
0,5 |
30 |
f(x)
= x4 |
t = x5 + 1 |
1 |
2 |
)
/
/
7. Записать в математической форме и вычислить пределы функций.
Вариант |
Функция 1 |
Функция 2 |
Функция 3 |
Функция 4 |
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
|
|
|
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
|
8. Записать в математической форме и вычислить предел функции f(х). Найти односторонние пределы (справа и слева). Построить график функции.
Вариант |
Функция |
Вариант |
Функция |
1 |
f(х) = ctg(x) x → 2π |
16 |
f(х) = cos(x)/x x → 0 |
2 |
f(х) = ctg(x) x → π |
17 |
f(х) = 1/ctg(x) x → π/2 |
3 |
f(х) = cos(x)/x x → 0 |
18 |
f(х) = 1/sin(x) x → 0 |
4 |
f(х) = 1/xe2x x → 0 |
19 |
f(х) = 1/tg(x) x → π |
5 |
f(х) = 1/x x → 0 |
20 |
f(х) = ctg(3x) x → 0 |
6 |
f(х) = ex/x x → 0 |
21 |
f(х) = tg(2x) x → π/4 |
7 |
f(х) = 1/cos(x) x → π/2 |
22 |
f(х) = ctg(x) x → π |
8 |
f(х) = ln(х)/x x → 0 |
23 |
f(х) = 1/xe2x x → 0 |
9 |
f(х) = 1/(x – 1) x → 1 |
24 |
f(х) = cos(x)/x x → 0 |
10 |
f(х) = tg(2x) x → π/4 |
25 |
f(х) = ctg(x) x → 2π |
11 |
f(х) = 1/sin(x) x → 0 |
26 |
f(х) = 1/x x → 0 |
12 |
f(х) = ctg(3x) x → 0 |
27 |
f(х) = ex/x x → 0 |
13 |
f(х) = cos(x)/x x → 0 |
28 |
f(х) = 1/cos(x) x → π/2 |
14 |
f(х) = 1/tg(x) x → π |
29 |
f(х) = ln(х)/x x → 0 |
15 |
f(х) = 1/ctg(x) x → π/2 |
30 |
f(х) = 1/(x – 1) x → 1 |
9. Исследовать функции на непрерывность в интервале от х1 до х2, включая крайние точки. Определить точки разрыва первого и второго рода, если они есть.
Вариант |
Функция |
х1 |
х2 |
Вариант |
Функция |
х1 |
х2 |
1 |
|
1 |
2 |
16 |
|
5 |
4 |
2 |
|
1 |
0 |
17 |
|
3 |
2 |
3 |
|
2 |
0 |
18 |
|
-5 |
-4 |
4 |
|
6 |
4 |
19 |
|
-1 |
0 |
5 |
|
5 |
4 |
20 |
|
1 |
2 |
6 |
|
-3 |
-2 |
21 |
|
0 |
1 |
7 |
|
4 |
5 |
22 |
|
1 |
2 |
8 |
|
1 |
2 |
23 |
|
-4 |
-3 |
9 |
|
4 |
2 |
24 |
|
1 |
0 |
10 |
|
3 |
2 |
25 |
|
-3 |
-2 |
11 |
|
-5 |
-4 |
26 |
|
4 |
5 |
12 |
|
-1 |
0 |
27 |
|
1 |
0 |
13 |
|
0 |
1 |
28 |
|
6 |
4 |
14 |
|
-4 |
-3 |
29 |
|
2 |
0 |
15 |
|
1 |
2 |
30 |
|
1 |
2 |
10. Найти экстремумы функции (на всей числовой прямой) и определить, какой из них минимальный, а какой максимальный. Построить график функции всей числовой прямой и на заданном интервале.
Вариант |
Функция |
Интервал |
Вариант |
Функция |
Интервал |
1 |
f(x) = x2 + x3 |
-1 .. 0 |
16 |
f(x) = x3ex+2 |
-5 .. 0,5 |
2 |
f(x) = x2 + x5 |
-0,8 .. 0,4 |
17 |
f(x) = x5 ln x |
0 .. 1 |
3 |
f(x) = 3x2 + 5x3 |
-0,5 .. 0,1 |
18 |
f(x) = 7x2 + 9x3 |
-2 .. 1 |
4 |
f(x) = x3ex |
-5 .. 0,5 |
19 |
f(x) = 8x2 + 3x3 |
-2 .. 1 |
5 |
f(x) = x2 + 2x3 |
-0,5 .. 0,1 |
20 |
f(x) = 5x2 + 2x5 |
1,5 .. 0,5 |
6 |
f(x) = x3 ln x |
0 .. 2 |
21 |
f(x) = x3e2x |
-5 .. 0,5 |
7 |
f(x) = x ln x |
0 .. 10 |
22 |
f(x) = 8x2 + 3x3 |
-2 .. 1 |
8 |
f(x) = 2x3 + 5x2 |
-2 .. 0,5 |
23 |
f(x) = x5 ln x |
0 .. 1 |
9 |
f(x) = x3e2x |
-5 .. 0,5 |
24 |
f(x) = 3x2 + 5x3 |
-0,5 .. 0,1 |
10 |
f(x) = x3 ln 2x |
0 .. 1 |
25 |
f(x) = x3ex |
-5 .. 0,5 |
11 |
f(x) = 8x2 + 3x3 |
-2 .. 1 |
26 |
f(x) = x2 + x3 |
-1 .. 0 |
12 |
f(x) = x3ex+2 |
-5 .. 0,5 |
27 |
f(x) = x ln x |
0 .. 10 |
13 |
f(x) = 7x2 + 9x3 |
-2 .. 1 |
28 |
f(x) = 2x3 + 5x2 |
-2 .. 0,5 |
14 |
f(x) = x5 ln x |
0 .. 1 |
29 |
f(x) = x3e2x |
-5 .. 0,5 |
15 |
f(x) = 5x2 + 2x5 |
1,5 .. 0,5 |
30 |
f(x) = x3 ln 2x |
0 .. 1 |
11. Записать в Maple функцию, состоящую из отдельных кусков, построить график, вычислить первую производную и построить график.
Вариант |
Функция |
Вариант |
Функция |
Вариант |
Функция |
1 |
|
11 |
|
21 |
|
2 |
|
12 |
|
22 |
|
3 |
|
13 |
|
23 |
|
4 |
|
14 |
|
24 |
|
5 |
|
15 |
|
25 |
|
6 |
|
16 |
|
26 |
|
7 |
|
17 |
|
27 |
|
8 |
|
18 |
|
28 |
|
9 |
|
19 |
|
29 |
|
10 |
|
20 |
|
30 |
|
12. Записать в математической форме и вычислить сумму и произведение. Результат вычислений представить в аналитическом виде и в виде десятичного числа с точностью до тысячных.
Вариант |
Сумма |
Произведение |
Вариант |
Сумма |
Произведение |
1 |
|
|
16 |
|
|
2 |
|
|
17 |
|
|
3 |
|
|
18 |
|
|
4 |
|
|
19 |
|
|
5 |
|
|
20 |
|
|
6 |
|
|
21 |
|
|
7 |
|
|
22 |
|
|
8 |
|
|
23 |
|
|
9 |
|
|
24 |
|
|
10 |
|
|
25 |
|
|
11 |
|
|
26 |
|
|
12 |
|
|
27 |
|
|
13 |
|
|
28 |
|
|
14 |
|
|
29 |
|
|
15 |
|
|
30 |
|
|
13. Решить неравенство
Вариант |
Неравенство |
Вариант |
Неравенство |
1 |
х2 + 15х + 70 ≥ 25 + х |
16 |
2х3 + 3х2 – 6х – 18 ≤ 5х + 3 |
2 |
3х2 – 6х + 1 ≥ 2х2 – х + 7 |
17 |
-4х2 – 5х + 10 ≥ 2х2 +2х + 5 |
3 |
х3 – 3х + х2 + 3 ≤ х2 + 1 |
18 |
5х3 – 15х – 2 ≥ 5х3 – 6х |
4 |
х3 – 2х2 – 3х + 1 ≥ -х2 – 2х |
19 |
х3 + 3х2 – х – 7 ≤ х3 + х2 – 6 |
5 |
2х2 – 9х – 21 ≥ 9 – 2х |
20 |
х3 + 3х2 – х – 7 ≤ х3 + х2 – 6 |
6 |
х3 + х2 + 6х – 18 ≤ х3 + 2х + 3 |
21 |
х2 + 15х + 70 ≥ 25 + х |
7 |
18 – 18х + х2 ≥ 3 – 2х |
22 |
4х2 – 15х + 15 ≥ -3х2 +2х + 5 |
8 |
4х2 – 15х + 15 ≥ -3х2 +2х + 5 |
23 |
х3 – 3х + х2 + 3 ≤ х2 + 1 |
9 |
х3 + 3х2 – х – 7 ≤ х3 + х2 – 6 |
24 |
3х2 – 6х + 1 ≥ 2х2 – х + 7 |
10 |
5х3 – 15х – 2 ≥ 5х3 – 6х |
25 |
10 – 6х + 2х2 ≥ 5 – 2х |
11 |
х3 – 3х + х2 + 3 ≤ х2 + 1 |
26 |
2х2 – 9х – 21 ≥ 9 – 2х |
12 |
2х3 + 3х2 – 6х – 18 ≤ 5х + 3 |
27 |
х3 + х2 + 6х – 18 ≤ х3 + 2х + 3 |
13 |
10 – 6х + 2х2 ≥ 5 – 2х |
28 |
18 – 18х + х2 ≥ 3 – 2х |
14 |
-4х2 – 5х + 10 ≥ 2х2 +2х + 5 |
29 |
х3 – 3х + х2 + 3 ≤ х2 + 1 |
15 |
х3 + 3х2 – х – 7 ≤ х3 + х2 – 6 |
30 |
х2 + 15х + 70 ≥ 25 + х |
14. Найти корни полинома
Вариант |
Полином |
Вариант |
Полином |
1 |
х4 + 8х3 + 17х2 – 2х – 24 |
16 |
х4 + 5х3 – 37х2 – 269х – 420 |
2 |
х4 + 2х3 – 13х2 – 14х + 24 |
17 |
х4 – 10х3 – 12х2 + 234х – 405 |
3 |
х4 + 11х3 + 35х2 + 13х – 60 |
18 |
х4 – 10х3 + 27х2 – 2х – 40 |
4 |
х4 + 5х3 – 37х2 – 269х + 420 |
19 |
х4 + 20х3 + 145х2 + 450х + 504 |
5 |
х4 + 10х3 + 3х2 – 94х + 80 |
20 |
х4 + 8х3 + 9х2 – 38х + 40 |
6 |
х4 + 12х3 + 23х2 – 48х – 108 |
21 |
х4 – 10х3 + 27х2 – 2х – 40 |
7 |
х4 – 27х2 – 14х + 120 |
22 |
х4 + 14х3 + 36х2 – 126х – 405 |
8 |
х4 + 20х3 + 145х2 + 450х + 504 |
23 |
х4 – 3х3 – 23х2 – 33х – 14 |
9 |
х4 + 8х3 + 9х2 – 38х + 40 |
24 |
х4 – 27х2 – 14х + 120 |
10 |
х4 + 14х3 + 36х2 – 126х – 405 |
25 |
х4 + 12х3 + 23х2 – 48х – 108 |
11 |
х4 + 5х3 – 37х2 – 269х – 420 |
26 |
х4 + 11х3 + 35х2 + 13х – 60 |
12 |
х4 + 2х3 – 53х2 – 54х – 504 |
27 |
х4 + 5х3 – 37х2 – 269х + 420 |
13 |
х4 – 10х3 + 27х2 – 2х – 40 |
28 |
х4 + 8х3 + 17х2 – 2х – 24 |
14 |
х4 – 10х3 – 12х2 + 234х – 405 |
29 |
х4 + 2х3 – 13х2 – 14х + 24 |
15 |
х4 – 3х3 – 23х2 – 33х – 14 |
30 |
х4 + 2х3 – 13х2 – 14х + 24 |