1.2 Дифференциальный оператор d
Для создания функций с производными может также использоваться дифференциальный оператор D. Часто он позволяет создавать более компактные выражения, чем функции diff и Diff. Дифференциальный оператор записывается в следующих формах:
D(f) или D[i](f)
где f – выражение или имя функции;
i – положительное целое выражение или последовательность.
Оператор D(f) просто вычисляет имя производной от f, поскольку в этой форме он эквивалентен unnaply(diff(f(x),x),x). В форме D(f)(х) эквивалентно diff(f(х),х).
Пример:
> D(cos^2);
Вычисление производной в точке:
> D(sin)(Pi);
-1
Дифференциальный оператор можно применять для дифференцирования функций ряда переменных по заданной переменной.
Пример:
> f:=(x,y,z)->x*exp(y)*z+ln(z);
> D[1](f);
> D[2](f);
> D[3](f);
> D[1,3](f);
2. Решение дифференциальных уравнений
Важное место в математических расчетах занимает решение дифференциальных уравнений. К нему, в частности, относится анализ поведения различных систем во времени (анализ динамики), а также вычисление различных полей. Maple позволяет решать как одиночные дифференциальные уравнения, так и системы дифференциальных уравнений как аналитически, так и в численном виде.
2.1. Решение системы простых дифференциальных уравнений
Для решения системы простых дифференциальных уравнений (задача Коши) используется функция dsolve в следующей форме:
dsolve(deqns,vars)
dsolve(deqns,vars,option)
где deqns – одно дифференциальное уравнение или система дифференциального уравнения первого порядка с указанием начальных условий;
vars – переменная, относительно которой ищется решение;
option – необязательный параметр, указывающий метод решения.
Параметр option задает один из методов решения:
- exact – аналитическое решение (принято по умолчанию);
- explicit – решение в явном виде;
- laplace – решение через преобразование Лапласа;
- series – решение в виде ряда с порядком указываемым значением переменной Order;
- numeric – решение в численном виде.
Пример:
Решить дифференциальное уравнение m y’’(x) – k y’(x) = 0 при начальных условиях у(0) = 0 и у(1) = 1.
> a:=m*diff(y(x),x$2)-k*diff(y(x),x);
> yx0:=y(0)=0,y(1)=1:
> dsolve({a,yx0},y(x));
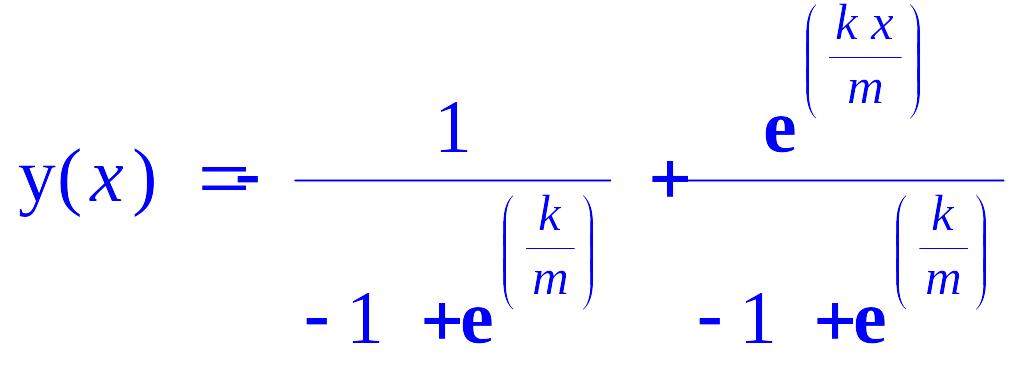
Пример:
Дана система дифференциальных уравнений:
.
Решить систему:
- аналитическим методом;
- методом разложения в степенной ряд до 8-го порядка;
> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);
> fons:=(y(0)=0,z(0)=1):
> dsolve({sys,fons},{y(x),z(x)});
> Order:=8: dsolve({sys,fons},{y(x),z(x)},series);
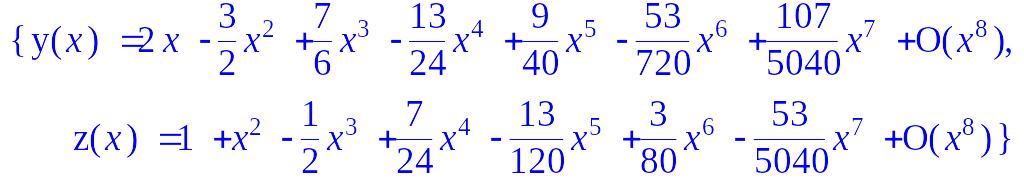
2.2. Численное решение дифференциальных уравнений
Для решения дифференциальных уравнений в численном виде используется функция dsolve с опцией numeric или type=numeric.При этом решение возвращается в виде специальной процедуры, по умолчанию реализующей широко известный метод решения дифференциальных уравнений Рунге-Кутта-Фельберга порядка 4 и 5 (в зависимости от условий адаптации решения к скорости его изменения). Эта процедура называется rkf45 и символически выводится (без тела) при попытке решения заданной системы дифференциальных уравнений.
Указанная процедура возвращает особый тип данных, позволяющий найти решение в любой точке или построить график решения (или решений). При этом используется функция plot[odeplot] из пакета odeplot, предназначенного для визуализации решений дифференциальных уравнений.
Пример:
Решить систему дифференциальных уравнений из предыдущего примера в численном виде при х = 2. Построить график решений.
> sys:=diff(y(x),x)=2*z(x)-y(x)-x,diff(z(x),x)=y(x);
> fons:=(y(0)=0,z(0)=1):
> de:=dsolve({sys,fons},{y(x),z(x)},numeric);
> de(2);
> plots[odeplot](de,[x,z(x)],0..2.5,labels=[x,z]);
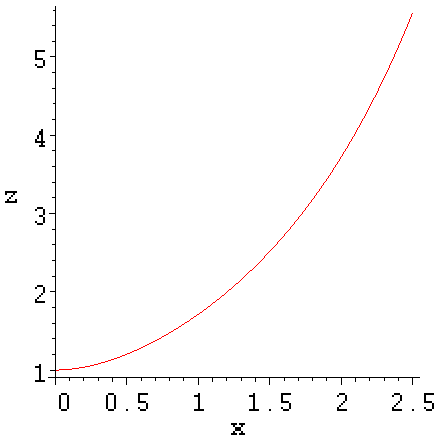
Рис. 1. График решения дифференциального уравнения в Maple
Можно построить на одном графике зависимости у(х) и z(х), представляющие полное решение заданной системы. При этом процедура имеет особый вид listprocedure и для преобразования листа выходных данных в векторы решения Y и Z используется функция subs.
Пример:
Решить систему уравнений и построить график решений.
> sys:=diff(y(x),x)=2*z(x)*sin(x)-y(x)-x, diff(z(x),x)=y(x);
> fons:={y(x),z(x)}:
> F:=dsolve({sys,y(0)=0,z(0)=1},fons,type=numeric,output= listprocedure);
> Y:=subs(F,y(x)):Z:=subs(F,z(x)):
> plot({Y,Z},0..6);
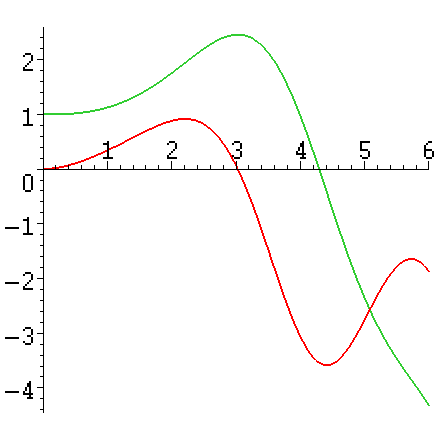
Рис. 2. График решения системы дифференциальных уравнений в Maple