1.3. Уклонения отвесных линий

Астрономо-геодезический метод определения поверхности Земли содержит два этапа: определение параметров поверхности относимости (референц-эллипсоида) и определение координат точек опорной геодезической сети относительно референц-эллипсоида. На обоих этапах используют систему геодезических координат B, L, H. Геодезические координаты текущей точки получают последовательным прибавлением приращений координат ΔB, ΔL, ΔH к координатам B₀, L₀, H₀ исходного пункта.

В процессе геодезических измерений вертикальную ось вращения прибора устанавливают по отвесной линии, кроме этого измерения выполняют на физической поверхности Земли. Поэтому непосредственно по результатам измерений получить приращения ΔB, ΔL, ΔH геодезических координат нельзя. Для их получения все измеренные в геодезической сети величины: горизонтальные направления, длины сторон, их азимуты редуцируют на поверхность референц-эллипсоида.

Разработку математически строгого метода редуцирования измеренных величин с физической поверхности Земли на поверхность референц-эллипсоида принято называть редукционной задачей, в России для ее решения исопльзуют предложенный в 1934 г. Ф.Н. Красовским метод проектирования. Проектирование измеренных величин осуществляют по нормалям к поверхности эллипсоида. Измеренные величины (направления, азимуты) связаны с отвесными линиями. Поэтому для редукции измеренных элементов необходимо знать уклонения отвесных линий на пунктах геодезической сети, а также высоты пунктов над эллипсоидом.

Угол между вектором g силы тяжести и вектором п нормали к земному эллипсоиду в точке Q называется уклонением отвесной линии (рис. 8). В зависимости от принятого эллипсоида различают абсолютные и относительные уклонения отвесных линий. Абсолютным (относительным) уклонением отвеса называется угол между отвесной линией и нормалью к общеземному эллипсоиду (референц-эллипсоиду).

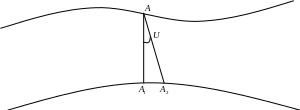
Рис.8. Уклонение отвесной линии

( - отвесная линия, -нормаль к поверхности эллипсоида)

Уклонение отвесной линии, определенное как угол между векторами g и п, называют астрономо-геодезическими уклонениями отвесных линий в отличие от гравиметрических, связанных с нормальным гравитационным полем Земли. Гравиметрическим уклонением отвеса называется угол между вектором g силы тяжести реального поля и вектором γ силы тяжести нормального поля.

Когда не требуется высокая точность в определениях, абсолютные астрономо-геодезические уклонения отвеса отождествляют с гравиметрическими, полагая, что за Нормальную Землю принят общеземной эллипсоид.

Астрономо-геодезическое уклонение отвесной линии (U) раскладывается на две составляющие ξ_аг, η_аг в плоскости меридиана и первого вертикала соответственно. Величины ξ_аг, η_аг связаны с астрономическими и геодезическими координатами зависимостями:

ξ_аг = φ – β;

η_аг = (π – L) cos β.

Уклонения отвесных линий при работах в горных районах должны быть известны для всех пунктов 1-3 классов. В астрономо-геодезической сети определяют астрономические широты φ и долготы λ на отдельных пунктах в среднем через 70-100 км. Вычислив для этих пунктов геодезические широты В и долготы L, определяют по вышеприведенным формулам искомые уклонения отвесных линий. Для промежуточных пунктов их определяют путем косвенного интерполирования полученных уклонений с учетом нелинейности их изменений между пунктами. Для этого выполняют гравиметрическую съемку местности по определенной программе и для всех пунктов вычисляют сначала гравиметрические уклонения отвесных линий ξ_гр, η_гр, а затем с учетом их находят искомые уклонения ξ_аг, η_аг.

Зная астрономо-геодезические уклонения отвесных линий ξ_гр, η_гр, и расстояния между пунктами, определяют превышения квазигеоида и его высоты над эллипсоидом (аномалии высот ζ). Определив в результате нивелирования нормальные высоты пунктов H_ν, вычисляют их геодезические высоты.