ВЫСШАЯ ГЕОДЕЗИЯ

1.Общие сведения

1.1. Форма и размеры Земли.

Земля является неправильным геометрическим телом, поверхность которого состоит из твердой оболочки на суше и из невозмущенной поверхности морей и океанов.

Суша составляет около 1/3 земной поверхности. Возвышается она над уровнем моря в среднем на 900 м, т.е. на очень малую величину по сравнению со средним радиусом Земли (R = 6371 км). Более 70% земной поверхности покрыто морями и океанами. Поэтому за фигуру Земли в первом приближении можно принять фигуру, ограниченную невозмущенной поверх­ностью морей и океанов и продолженную под материками так, чтобы отвесные линии во всех ее точках были перпендикулярны к ней. Такую фигуру Земли по предложению немецкого физика Листинга называют геоидом. Изучением геоида геодезисты занимаются более ста лет. В настоящее время на акватории Мирового океана геоид с высокой точностью (до 0,1-0,3 м по высоте) изучают методом спутниковой альтиметрии, измеряя расстояния от спутника до подспутниковых точек на поверхности морей и океанов.

При изучении фигуры геоида на суше метод спутниковой альтиметрии не работает, а другие методы космической геодезии дают недостаточную точность определения его поверхности. Для того чтобы изучить фигуру геоида по наземным измерениям с высокой точностью, необходимо силу тяжести измерять непосредственно на его поверхности, что не осуществимо. По результатам комплекса наземных астрономо-геодезических и гравиметрических измерений теоретически безупречно может быть определена другая вспомогательная поверхность, получившая название поверхности квазигеоида, которая незначительно отклоняется от поверхности геоида: в равнинной местности на 2-4 см, а в горах не более 2 м. На морях и океанах поверхности геоида и квазигеоида совпадают. Фигуру Земли, ограниченную этой поверхностью, называют квазигеоидом.

Определив из обработки наземных измерений параметры квазигеоида и измерив относительно него высоты точек земной поверхности, можно теоретически строго изучить фигуру реальной Земли, ограниченную ее твердой оболочкой на суше и невозмущенной поверхностью морей и океанов.

При изучении фигуры Земли с давних пор поступают следующим образом. Сначала определяют форму и размеры некоторой модели Земли, поверхность которой сравнительно проста, хорошо изучена в геометрическом отношении, удобна для решения на ней разнообразных задач геодезии и картографии и наиболее полно характеризует в первом приближении форму и размеры реальной Земли. Затем, приняв поверхность этой модели Земли за отсчетную, определяют относительно нее высоты точек поверхности изучаемой фигуры - геоида (квазигеонда) или реальной Земли - и таким образом получают данные, характеризующие форму и размеры конкретной фигуры.

При решении задач высшей геодезии за такую модель Земли принимают эллипсоид вращения с малым полярным сжатием, называемый общим земным эллипсоидом (рис. 1). Его поверхность может быть получена вращением полуэллипса PEP₁ вокруг его малой оси РР₁.

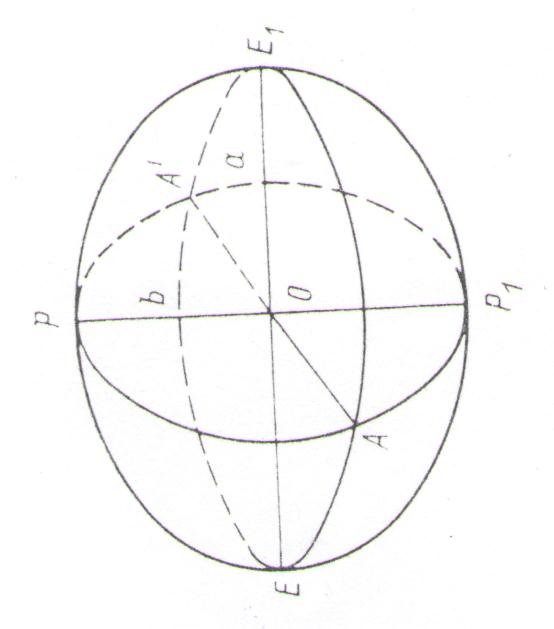
Рис.1. Земной эллипсоид

Форма и размеры земного эллипсоида характеризуются большой a и малой b полуосями, а чаще большой полуосью а и полярным сжатием α,

или большой полуосью а и первым эксцентриситетом е меридианного эллипса:

.

Для того чтобы общий земной эллипсоид возможно точнее характеризовал форму и размеры всей Земли, его параметры a, α определяют с учетом следующих условий:

1) центр общего земного эллипсоида должен совпадать с центром масс Земли, а его малая ось - с осью вращения Земли;

2) объем эллипсоида должен быть равен объему геоида (квазигеоида);

3) сумма квадратов отклонений no высоте эллипсоида от поверхности геоида (квазигеоида) должна быть наименьшей.

В течение полутора веков ученые многих стран занимались определением размеров земного эллипсоида, используя имеющиеся в разном объеме разной точности и содержания градусные измерения. Приведем некоторые результаты таких определений (табл. 1).

Таблица 1

Ученый	Государство	Год	a, м	α, м
Деламбр	Франция	1800	6 375 653	1 : 334,0
Бессель	Германия	1841	6 377 397	1 : 299,2
Кларк	Великобритания	1866	6 378 206	1 : 294, 98
Хейфорд	США	1910	6 378 388	1 : 297
Красовский	СССР, Россия	1940	6 378 245	1 : 298,3

Эллипсоид Бесселя, кроме Германии и ряда других стран, применялся также и в Советском Союзе вплоть до 1942 г., когда начался переход к эллипсоиду Красовского.

Эллипсоид Кларка (1866 г.) применяется в США, странах Латинской и Центральной Америки, включая Кубу, а также в ряде других стран.

Эллипсоид Хейфорда используется в ряде европейских стран. Он в 1942 г. в Мадриде на II Генеральной ассамблее Международной ассоциации геодезии был рекомендован в качестве международного. Параметры этого эллипсоида выведены из градусных измерений, выполненных только на территории США, и содержат значительные ошибки. В этом легко убедиться, если сравнить параметры эллипсоида Хейфорда с параметрами земного эллипсоида, полученными в результате обработки спутниковых наблюдений: а = 6 378 137 м, α = 1 : 298, 257.

Эллипсоид Красовского является наиболее точным из всех эллипсоидов, полученных из обработки наземных измерений. Его размеры близки к размерам общего земного эллипсоида, полученным по данным наблюдений ИСЗ: сжатие практически одинаковое, а большие полуоси отличаются всего лишь на 108 м. Эллипсоид Красовского применяется в России и в ряде других стран.

Фигура и гравитационное поле Земли тесно взаимосвязаны и их изучение представляет собой по существу одну задачу. Сложная структура гравитационного поля, обусловленная неправильностями фигуры Земли и особенностями распределения плотностей масс, создает значительные трудности при определении потенциала силы тяжести W. Задача определения потенциала W существенно облегчается, если гравитационное поле Земли представить в виде двух полей: основного, или нормального и остаточного, или аномального и каждое из них изучать отдельно.

За физическую модель Земли при этом принимают так называемый уровенный эллипсоид вращения, внешняя поверхность которого является уровенной и сила тяжести в каждой точке ее направлена по нормали к ней.

Центр уровенного эллипсоида совмещают с центром масс Земли, а ось его вращения - с осью вращения Земли. Гравитационное поле, создаваемое уровенным эллипсоидом на его поверхности и во внешнем пространстве, называют нормальным гравитационным полем, а силу тяжести нормальной и обозначают буквой γ.

Уровенный эллипсоид, принимаемый за физическую модель Земли при определении ее фигуры и гравитационного ноля, принято называть Нормальной Землей.

При решении геодезических задач в масштабе всей Земли за поверхность относимости целесообразно принять поверхность общего земного эллипсоида (Нормальной Земли). При решении топографо-геодезических и картографических задач в пределах одной или группы стран каждое государство за поверхность относимости обычно принимает земной эллипсоид, имеющий определенные размеры и ориентировку в теле Земли, называемый референц-эллипсоидом.

Форму, размеры и ориентировку референц-эллипсоида определяют, соблюдая следующие требования:

1) параметры референц-эллипсоида должны возможно меньше отличаться от параметров общего земного эллипсоида;

2) ось вращения референц-эллипсоида должна быть параллельна оси вращения Земли, а плоскость его экватора - плоскости экватора Земли;

3) в пределах территории страны или группы стран, для которой подбирается референц-эллипсоид, сумма квадратов отклонений поверхности квазигеоида (геоида) от поверхности референц-эллипсоида должна быть наименьшей.

В СССР до 1942 г. при топографо-геодезических и картографических работах применялся референц-эллипсоид Бесселя. В начале тридцатых годов проф. Ф.Н. Красовский, обрабатывая ряды триангуляции 1 класса от Прибалтики до Дальнего Востока, обнаружил, что по мере удаления на восток систематически возрастают величины уклонений отвесных линий. Это указывало на то, что большая полуось эллипсоида Бесселя определена недостаточно точно и поэтому для огромной территории СССР, простирающейся по долготе почти на 150⁰, эллипсоид Бесселя не подходит.

Используя градусные измерения, выполненные в СССР, странах Западной Европы и США, а также, учитывая данные гравиметрической съемки в СССР проф. Ф.Н. Красовский при участии проф. А.А. Изотова к 1940 г. вывел новые, самые точные по тому времени параметры земного эллипсоида: а = 6 378 245 м, α = 298,3, которые незначительно отличаются от современных данных.

Земной эллипсоид с этими размерами в 1946 г. был утвержден в качестве национального референц-эллипсоида для территории СССР.

Столь же надежно с использованием большой астрономо-геодезнческой сети СССР осуществлено ориентирование эллипсоида Красовского путем установления исходных геодезических дат - определения координат начального пункта геодезической сети страны и исходного азимута. В качестве последних приняты координаты центра Круглого зала Пулковской обсерватории и геодезический азимут с сигнала А на пункт Бугры Саблинской базисной сети. Высота геоида над поверхностью референц-эллипсоида в Пулково принята равной нулю.

Указанные исходные геодезические даты и эллипсоид Красовского в качестве координатной поверхности образуют системы координат 1942, 1995гг. (СК-42, СК-95), принятые в СССР, а в настоящее время в России.