4. Построение расчетной схемы, типы конечных элементов

Привести внятные и однозначные рекомендации по выбору и построению расчетных схем сооружений различного назначения, обладающих разными конструктивными решениями, практически невозможно. Это, по-видимому, можно сделать, лишь ограничившись гораздо более узким классом объектов. Нужно помнить, что любой набор правил для построения моделей может, в лучшем случае, иметь только ограниченную область применения, а в худшем случае – даже помешать проявлению необходимой интуиции.

В силу сказанного, все, что приведено ниже, нужно рассматривать, во-первых, только как очень мягкие рекомендации и, во-вторых, заранее настроиться на отрывочный стиль изложения.

Но прежде, чем переходить непосредственно к рекомендациям, имеет смысл обратить внимание на следующий аспект в построении расчетной схемы. Расчетная схема интересует инженера не сама по себе, а в качестве промежуточной модели для определения напряженно-деформированного состояния конструкции, для оценки инженером таких показателей конструкции как ее способность быть возведенной, надежно эксплуатируемой, экономичной и т.д. В этой связи, в процессе получения результирующей информации расчет условно можно разбить на четыре шага (Рис.5).

Первый шаг – переход от реальной конструкции к ее математической модели. Второй шаг – переход от математической модели к расчетной модели, приспособленной к возможностям конкретного инструмента вычислений. Третий шаг – описание этой расчетной схемы доступными средствами избранного программного обеспечения, проведение самого расчета, получение численных результатов расчета. И, наконец, последний шаг связан с интерпретацией и анализом результатов расчета и получением итоговой информации.

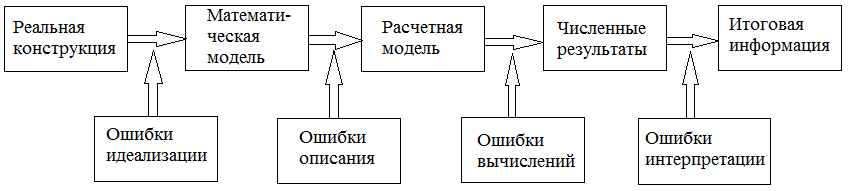
Рис.5. Погрешности на разных шагах расчета.

На каждом из этих шагов роль или степень участия инженера-расчетчика и роль используемого программного обеспечения различны, равно как и различна их ответственность. Важно обратить внимание на то, что каждый из этих шагов содержит элементы моделирования, а значит – вносит и свою долю в накопление погрешностей при переходе от реальной конструкции к итоговой информации.

4.1. Определяющие параметры и число степеней свободы

В последнее время наблюдается явно выраженная тенденция все большего усложнения используемых расчетных схем и увеличения их размерности.

Расчетные задачи большой размерности совершенно естественно возникают при анализе трехмерных проблем механики сплошной среды в конечно-элементной постановке. Размер такой задачи может быть до десятков тысяч неизвестных даже в случае областей, не слишком отличающихся от канонических. Именно такие пространственные задачи порождают естественный спрос на программы большой мощности, и для удовлетворения подобного спроса разработчики непрерывно наращивают их возможности. Однако затем эти программные продукты используются и при решении задач расчета стержневых несущих каркасов, создавая соблазн для расчетчика применить подробную расчетную схему каркаса, включающую в себя десятки тысяч упругих элементов и узлов.

Казалось бы, что никакой разницы в двух описанных выше случаях нет. Однако, это не так. Задача механики сплошной среды для своего описания требует только аккуратного задания геометрии тела, а характеристики материала задаются несколькими параметрами. Для сложного стержневого каркаса массив исходных параметров весьма велик и разнороден. Большинство таких параметров, по сути, являются случайными величинами, для которых расчетчик задает лишь некоторую возможную реализацию значений. Поэтому с увеличением числа задаваемых параметров возрастает степень неопределенности расчетной модели в целом.

У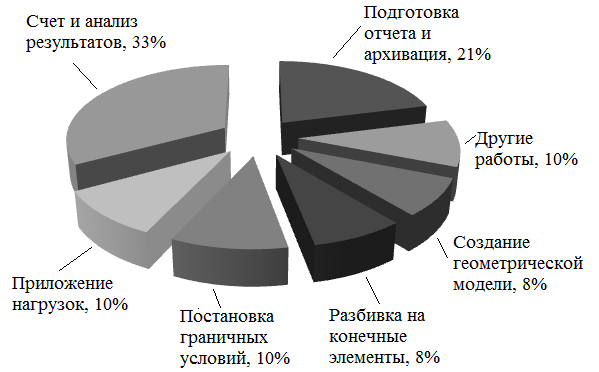 величение размерности задач приводит к резкому росту трудозатрат на подготовку исходной информации и на анализ результатов. На Рис.6 представлены усредненные данные о распределении трудозатрат при использовании известной системы ANSYS, специально предназначенной для решения больших задач.

Рис.6. Распределение затрат труда.

Эти данные хорошо иллюстрируют тот факт, что работа с данными о расчетной схеме занимает большой объем (36%) трудозатрат (создание геометрической модели – 8%, разбивка на конечные элементы – 8%, постановка граничных условий – 10%, приложение нагрузок – 10%). И для экономии труда требуется возможно более тщательное обоснование разумной степени сложности расчетных моделей.

Но дело не только в росте трудозатрат на подготовку данных и анализ результатов. Порой формальная разбивка конструкции в дискретной расчетной схеме на «лапшу» из тысяч конечных элементов приводит лишь к кажущейся эффективности и повышению точности в решении задачи. На самом деле точность может существенно понизиться в связи с неизбежным наращиванием погрешностей вычислений при увеличении по порядку количества неизвестных в дискретной схеме. Вряд ли разумно разбивать стержни стержневого каркаса здания на трехмерные конечные элементы.

Идея МКЭ в самом общем виде заключается в разделении исследуемой области (конструкции) на ряд более мелких подобластей (конечных элементов) несложной геометрической формы – стержень, треугольная или четырехугольная пластинка, тетраэдр, призма и т. п. Вершинами таких конечных элементов являются узлы – абсолютно жесткие тела бесконечно малых размеров. Положение узла в пространстве определяется шестью координатами (степенями свободы) – три линейных перемещения по координатным осям и три угла поворота относительно этих же осей. Именно в узлах (и только в узлах!) элементы предполагаются соединенными между собой. При этом могут быть реализованы различные варианты сопряжений как элементов друг с другом, так и элементов с узлами.

Построение расчетной схемы всегда есть определенный компромисс. Чтобы с помощью этой схемы можно было получить результаты, имеющие смысл и прикладное значение, она должна быть достаточно детальной и сложной. В то же время, она должна быть достаточно простой, чтобы можно было получить решение при таких ограничениях, как сроки, доступное программное обеспечение, квалификация исполнителей, возможности анализа и осмысления получаемых результатов, а также адекватной по точности исходной модели.

Подавляющее число достижений теории сооружений связано с тем, что удавалось выделить объекты с относительно небольшим числом определяющих параметров, взаимодействие отдельных частей которых было относительно слабым. Для таких систем можно сформулировать и решить задачу в такой постановке, когда отыскивался «полный ответ», то есть детальная картина напряженно-деформированного состояния всех элементов системы. Такая постановка задачи настолько укоренилась в расчетной практике, что считалась единственно возможной и без критического анализа переносилась на большие системы.

К числу наиболее мощных приемов упрощения принадлежит использование некоторых кинематических гипотез, с помощью которых поведение больших групп «независимых» переменных представляется через относительно небольшое число определяющих параметров. Типичным примером является использование гипотезы плоских сечений в теории стержней Бернулли-Эйлера.

Аналогичны гипотезы об отсутствии деформаций в плоскости перекрытий многоэтажного здания, когда они представляются абсолютно жесткими диафрагмами, а здание в целом рассчитывается на горизонтальные нагрузки как система соединенных упругими вертикальными связями горизонтальных дисков, движущихся только в горизонтальной плоскости. Все эти приемы агрегирования переменных и использования некоторых обобщенных координат важны не столько для уменьшения размерности задачи, сколько для сжатия информации с целью большего удобства ее осмысления. Кроме того, такие приемы важны в тех случаях, когда данные о внешних воздействиях не детализированы в такой степени, чтобы их можно было корректно «привязать» к детальной расчетной схеме.