3. Принципы автоматизации проектирования

Современные строительные объекты чаще всего - довольно сложные конструктивные многоэлементные системы, создаваемые для выполнения большого числа различных функций. Их жизненный цикл связан с возможностью реализации многих рабочих состояний. Сами же объекты должны сочетать в себе противоречивые требования: функциональность, конструктивность, эстетичность, экономичность.

Основными этапами компьютерного расчета являются:

- создание модели;

- выбор программного обеспечения для реализации расчета;

- проверка модели;

- собственно расчет;

- верификация результатов.

Все требования к строительным объектам невозможно и некорректно учесть в одной расчетной модели (динамика – более полная модель по сравнению, например, со статикой). Это первая особенность проблемы моделирования. Вторая особенность – многомерность применяемых расчетных моделей с общей тенденцией ко все большей их детализации и рассмотрении процесса работы во времени. Например, конечноэлементная модель здания (Рис.1) может содержать десятки тысяч узлов и конечных элементов.

Рис1. Конечноэлементная модель здания.

Для возможности расчета какой-либо конструкции методом конечных элементов прежде всего необходимо создать ее виртуальную модель, которая будет в дальнейшем анализироваться математическим образом и для которой будут выявляться определенные внутренние закономерности ее напряженно-деформированного состояния. Такую модель называют расчетной моделью, и по ее поведению судят о поведении моделируемой реальной конструкции.

Достаточно часто в литературе помимо понятия «расчетная модель» встречается также понятие «расчетная схема».

При расчетах с применением МКЭ под расчетной схемой подразумевают набор данных, включающий информацию о геометрии анализируемой конструкции, характере сопряжения ее отдельных элементов между собой и с «землей» (условия ее закрепления), приложенных нагрузках, а также материала, из которого выполнены ее отдельные части. В совокупности расчетная схема является некоторым целостным виртуальным понятием, которому при желании может быть придана геометрическая интерпретация в виде наглядного рисунка.

Расчетная модель отличается от расчетной схемы тем, что содержит еще и дополнительную информацию относительно методологии проведения расчетного анализа, т. е. нужно ли в дальнейшем вести расчет в линейной или нелинейной постановке, нужно ли учитывать какие-то специфические условия работы отдельных частей схемы, как, например, равенство перемещений ее отдельных узлов или совместность работы ее отдельных элементов и т. д.

Расчетная схема не содержит такой информации, она предоставляет лишь исходные данные для расчета. Модель же предполагает и наличие элементов дальнейшего анализа поведения исследуемой конструкции под нагрузкой.

Таким образом, расчетная модель является понятием более общим, и при ее создании сначала формируется именно расчетная схема, которая в дальнейшем перерастает в модель. В свою очередь, анализироваться должна только расчетная модель, а не расчетная схема, и все приводимые выводы и рекомендации должны относиться также только к ней.

Примером учета совместной работы отдельных элементов схемы может быть рамное каркасное здание на Рис.2. Расчет сооружений на воздействия неравномерных деформаций основания целесообразно производить в нелинейной постановке. При нелинейном расчете сооружений на воздействие деформаций основания целесообразно принимать условие прочности сечений конструкций в виде уравнения, включающего допускаемые (или предельные) д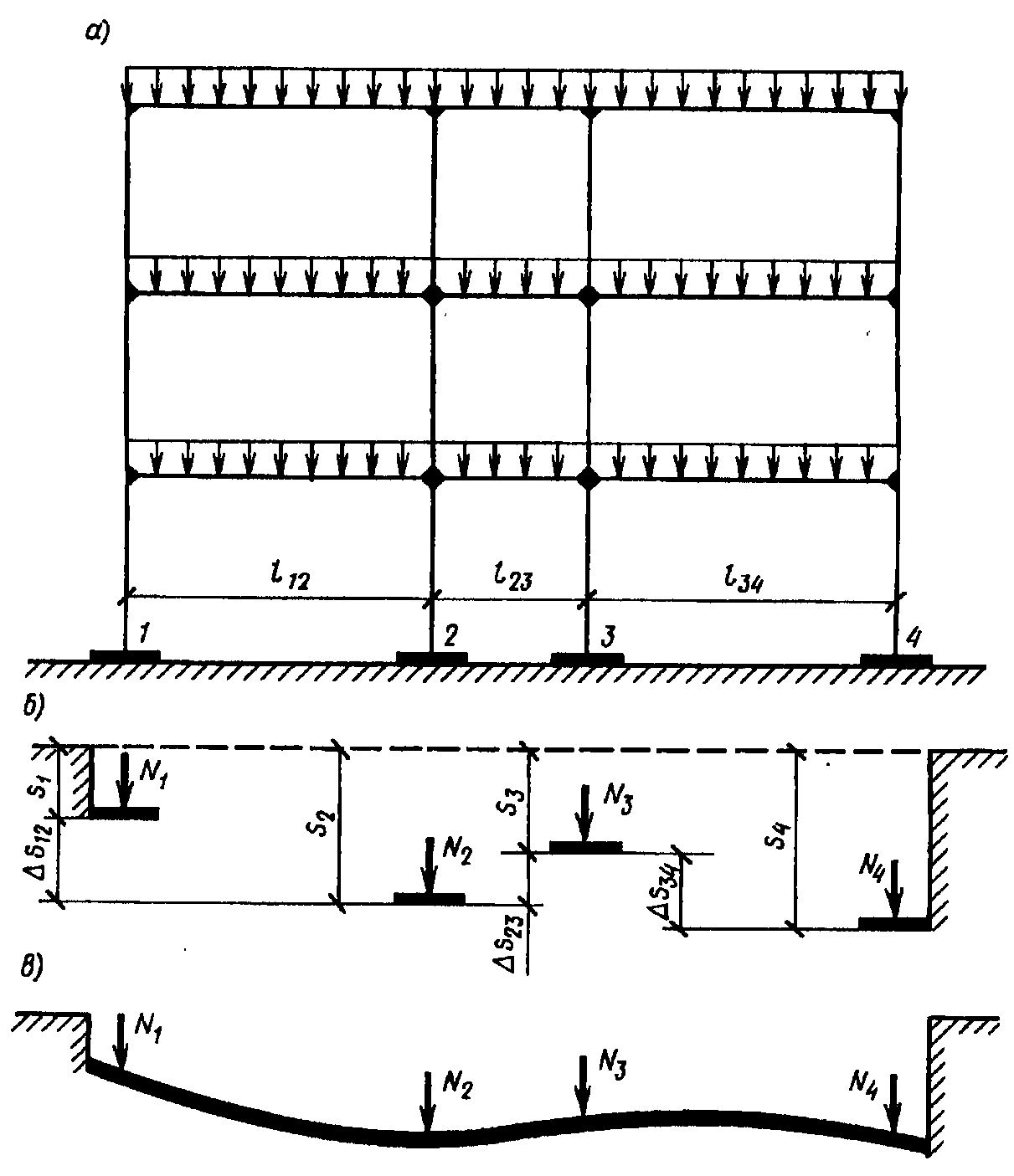 еформации материалов, а не их прочностные характеристики.

Рис.2. Осадки фундаментов каркасного здания: а) – расчетная схема каркаса; б) – осадки и разности осадок отдельных фундаментов; в) – осадки ленточного фундамента.

Чтобы выяснить необходимость выполнения расчета сооружения во взаимодействии с основанием, сначала определяются допускаемые и предельные деформации сооружения, затем по этим данным находятся допускаемые и предельные деформации основания. Разности осадок смежных фундаментов составляют Ds₁₂, Ds₂₃, Ds₃₄ ; соответствующие перекосы Ds₁₂ / l₁₂, Ds₂₃ / l₂₃, Ds₃₄ / l₃₄. При сопоставлении полученных перекосов с допускаемыми и предельными их значениями (по нормам проектирования) делается вывод о необходимости расчета сооружения во взаимодействии с основанием.

Учет нелинейной работы конструкций позволяет более достоверно устанавливать фактическое распределение жесткостей в элементах сооружений и на этой основе снижать расчетные значения усилий в наиболее нагруженных сечениях по сравнению с линейно-упругим расчетом. К решению нелинейных задач имеются различные подходы, однако все они основаны на тех или иных итерационных процессах. Основной частью такого процесса является вычисление жесткостных характеристик элементов конструкций и основания по известным из предыдущего этапа расчета усилиям по перемещениям и определение усилий и перемещений в линейно деформируемой системе (т.е. нагрузка разбивается на ряд ступеней, на каждой из которых проводится линейный расчет с учетом имевшегося загружения). Виды нелинейной работы конструкций: физическая нелинейность (грунты основания), геометрическая нелинейность (вантовые сооружения, мембраны), конструктивная нелинейность (расчет сооружения в процессе монтажа).

Необходимость учета последовательности монтажа можно проиллюстрировать на простом примере расчета двухпролетной трехэтажной рамы (Рис.3). При монтаже каждого этажа ригель присоединяется к стойкам шарнирно и несет при этом нагрузку 2,0 т/м. Затем узлы присоединения ригелей омоноличиваются и ригели догружаются весом плит перекрытия, которые создают дополнительную нагрузку 2,0 т/м. Так монтируются все этажи.

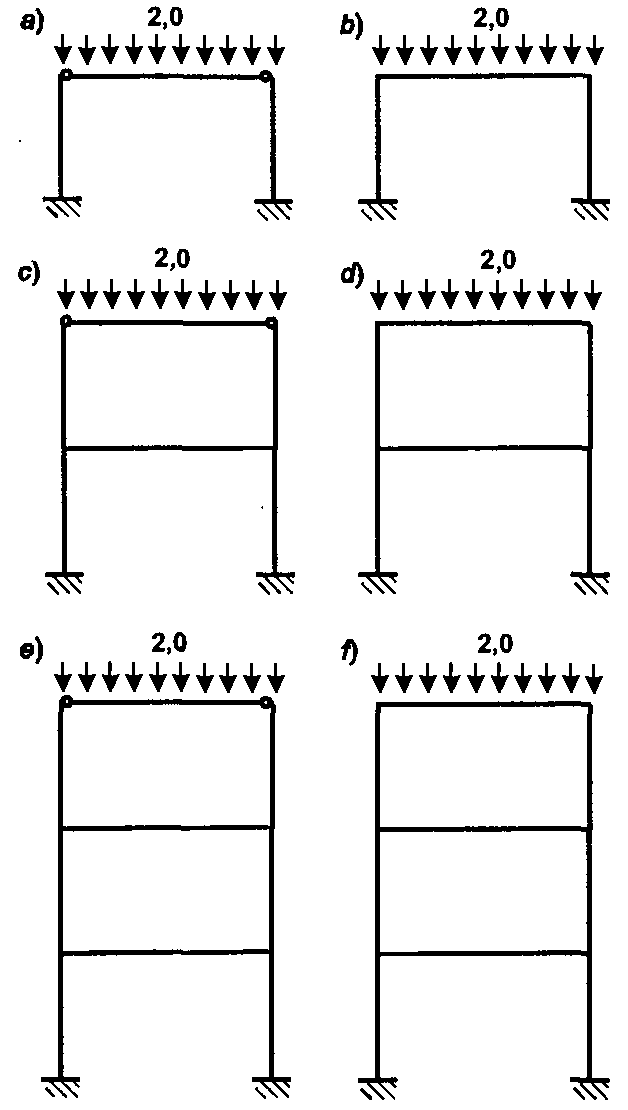
Рис.3 Монтажные состояния плоской рамы

Последовательный расчет конструкции на стадиях монтажа а)…f) и суммирование полученных результатов дают эпюру изгибающих моментов, представленную в левой части Рис.4. Для сравнения справа приведена эпюра моментов, которая была бы получена в полностью готовой системе, если бы к ее ригелям была приложена нагрузка 4,0 т/м.

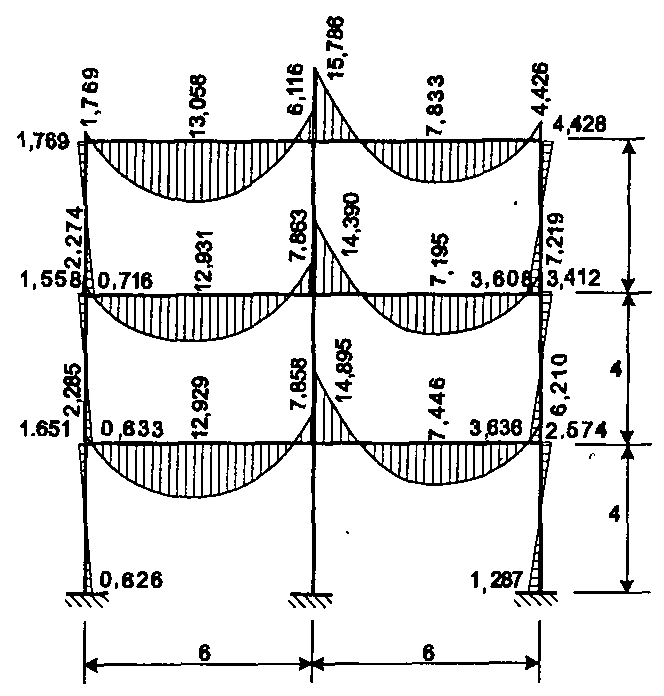
Рис.4 Сопоставительные эпюры моментов в раме.

От правильности создания расчетной модели, в конечном счете, зависит и правильность делаемых в дальнейшем выводов и приводимых рекомендаций.