4.5. Дискретизация модели

Большое значение в создании расчетной модели при расчете по МКЭ имеет вопрос о дискретизации, т.е. разбивке на конечные элементы. К сожалению, в настоящее время не существует каких-либо универсальных теоретических разработок касательно выбора конечно-элементной сетки. Все рекомендации сводятся, во многом, к полуформальным закономерностям, которые также бывает сложно применить в какой-либо конкретной ситуации. На их основе, в свою очередь, разработаны некоторые полуэмпирические рекомендации, которые также, хотя и носят довольно общий характер, но уже могут быть практически применены.

Наиболее важные из них следующие:

1. Для стержневых конечных элементов имеются точные аппроксимирующие решения, точно описывающие поле перемещений. При этом длина стержневого конечного элемента может быть любой, что никак не сказывается на точности решения. Однако, это верно лишь для статической линейной задачи при постоянной жесткости по длине стержня. Во всех остальных случаях исходный конструкционный стержень необходимо разбивать на более мелкие стержни – стержневые конечные элементы. При этом необходимые проверки (по СНиП на устойчивость и др.) следует выполнять для конструкционного стержня, а не для каждого конечного элемента.

2. Для континуальных систем имеется огромное количество работ, регламентирующих оценку сходимости для конкретного конечного элемента или их сочетаний (плита, оболочка, вплоть до конкретного вида конструкций). В настоящее время существует лишь общее правило дискретизации на конечные элементы: для получения инженерной точности решения 5% нужно выбрать шаг сетки равным примерно 1/20 от характерного размера.

Это положение выведено на основе некоторых наихудших предположений о сходимости. Поэтому, на практике приемлемая точность решения может быть получена на более крупной сетке конечных элементов. Для ответа на вопрос «какой?» используется прием последовательного сгущения сетки. Опыт показывает, что во многих случаях достаточным является принимать размер конечного элемента в пределах 1/10 – 1/8 характерного размера, а в некоторых случаях и еще крупнее. При этом внимание следует обращать на устойчивость решения, что является необходимым, но все-таки, недостаточным условием правильности решения. Оценку сходимости следует выполнять не только по перемещениям (они имеют наилучшую сходимость), но и по внутренним усилиям и напряжениям.

3. При решении задач устойчивости достаточным может считаться принять размер конечного элемента из такого расчета, чтобы в полуволну формы изгиба при потере устойчивости попадало 3 – 4 элемента.

4. При решении динамических задач считается, что надежно может быть вычислено то количество первых собственных частот системы и соответствующих им форм колебаний, которое равно примерно половине количества динамических степеней свободы системы. В большинстве случаев каждый узел сетки конечных элементов добавляет одну динамическую степень свободы. Поэтому, если например, требуется вычислить 30 первых частот для какой-либо конструкции, то она должна быть разбита на сетку конечных элементов, содержащую не менее 60 узлов. При этом вполне уместным оказывается применение правила п. 3 с прочтением его относительно полуволны формы колебаний.

5. Одним из основных принципов дискретизации является сгущение сетки конечных элементов в зоне выявленных концентраторов напряжений. Это же относится и к местам приложения сосредоточенной нагрузки, постановки жестких связей (особенно запрещения угловых перемещений), вокруг отверстий, вырезов, углов и т.д.

К специальным приемам относится и подбор густоты сетки, исходя получаемого в ходе анализа градиента напряжений. В современных программных комплексах очень часто эта операция выполняется автоматически по мере расчета. Основное внимание при этом должно быть обращено на гладкость конечно-элементной сетки (постепенное изменение размеров элементов).

6. Если в используемой программе отсутствует возможность сглаживания, то выполняя его вручную (Рис.7 ), рекомендуется переходную зону поделить на так называемые «фронты сгущения», располагаемые не чаще, чем через 2 – 3 ряда конечных элементов.

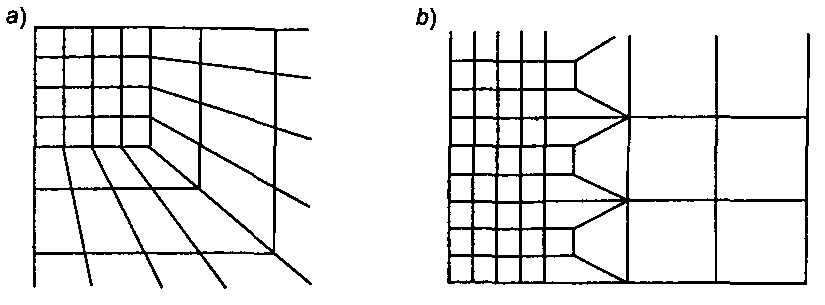
Рис.7. Приемы сгущения сетки четырехугольными элементами.

На одном таком «фронте» шаг сетки следует уменьшать не более, чем в два раза (Рис.8).

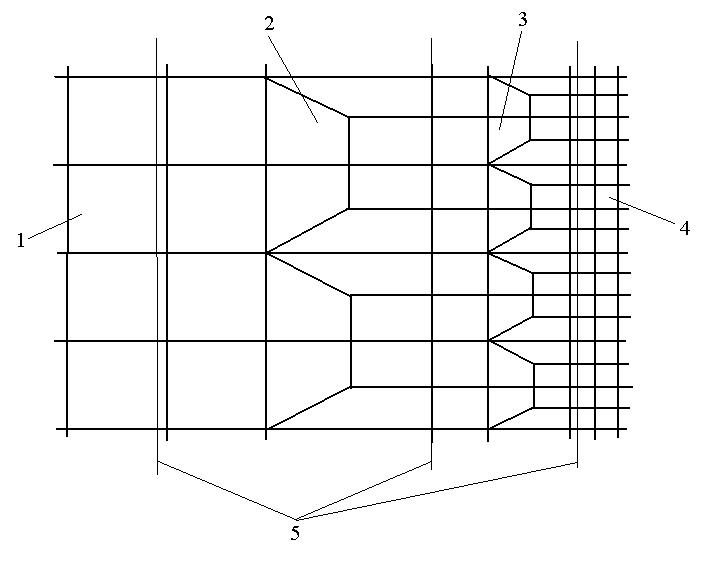
Рис.8. Переходная зона от одной густоты сетки к другой:

1 – сетка исходной густоты, 2 – I «фронт сгущения», 3 – II «фронт сгущения», 4 – сетка требуемой густоты (в 4 раза мельче), 5 – границы «фронтов сгущения»

7. Форма континуальных конечных элементов должна максимально быть приближенной к правильной (квадрат, куб, тетраэдр). При этом достигается наибольшая точность результатов. В различных конечных элементах соотношение сторон может варьироваться примерно до 1:4 – 1:5 без потери точности решения. Однако, это справедливо отнюдь не для всех типов конечных элементов и применимо только в областях с небольшим градиентом деформаций.

8. Следует максимально избегать, так называемой, «игольчатой» формы конечных элементов, представляющей собой четырехугольник с большим соотношением сторон (порядка 1:10) или треугольный конечный элемент с одним из углов порядка 1 - 10. Их применение серьезно искажает конечные результаты, приводя к существенной потере точности решения в рассматриваемой области.

9. Имеются конечные элементы, заведомо дающие плохую точность - треугольные конечные элементы с линейной аппроксимацией. Их математическая модель построена таким образом, что по всему элементу получаются постоянные значения напряжений (наблюдается, так называемое, кусочно-постоянное поле напряжений). Это вносит определенную погрешность в картину распределения напряжений в анализируемой области. Степень такой погрешности будет находиться в обратной зависимости от размеров элементов и их количества в этой области. Сгущение сетки конечных элементов, как правило, также лучше выполнять без использования треугольных элементов, например, по схеме, приведенной на рис. 8. Поэтому есть тенденция избегать применения треугольных и пирамидальных элементов, и создавать сетки из четырехугольных элементов и из объемных гексаэдров («кирпичей»), так как они обычно дают более точное решение по сравнению с треугольными и пирамидальными элементами.

Эти правила являются достаточно простыми, легко запоминающимися и в то же время универсальными. Их справедливость подтверждается огромным количеством самых разнообразных источников.