55 Особенности прочностного расчета зубьев конических колес

  

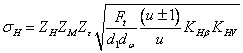
Используем связь тригонометрических функций для определе­ния передаточного числа и делительного диаметра эквива­лентного колеса  .

После подстановки в исходную формулу значений   и   и несложных преобразований получим формулу проверочного расчета для стальных пря­мозубых конических колес

                       

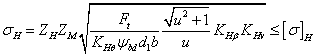
или, заменив  ;  ,  получим:

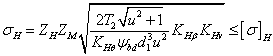
Па^1/2 (для стальных колес),                             

где  — возникающее нормальное контактное напряжение, МПа;   — средний делительный диаметр шестерни, мм;   — вращающий момент на колесе, Нмм;   — коэффициент, учитывающий форму сопряжения по­верхности зубьев;   — коэффициент, учитывающий механические свойст­ва материала;   — коэффициент ширины (длины) зуба;   — передаточное число;   = 0,85 — коэффициент, учитывающий снижение контактной прочности конической передачи по сравнению с прямозубой;   — допускаемое контактное напряжение. Из двух значе­ний   выбирается меньшее.

Проектировочный расчет.

Решая уравнение (31) относительно   запишем

                                                                          

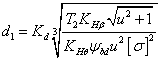
где   — вспомогательный коэффициент (для стальных прямозубых конических колес K_d =78 МПа^1/3).

56. Геометрия и кинематика червячных передач.

Червячная передача предназначена для сообщения вращательного движения валам, оси которых скрещиваются под углом 90 градусов. Движение осущ-ся по принципу винтовой пары, винтом является червяк, а колесо представляет собой узкую часть длинной гайки изогнутой по окружности резьбой наружу.  Преимущества:

• большие передаточные отношения;

• плавность и бесшумность  работы;

• высокая кинематическая точность;

• самоторможение.

Недостатки:

• низкий ККД;

• износ, заедание;

• использование дорогих материалов;

• требования к высокой точности сборки

Основные параметры и передаточное число:

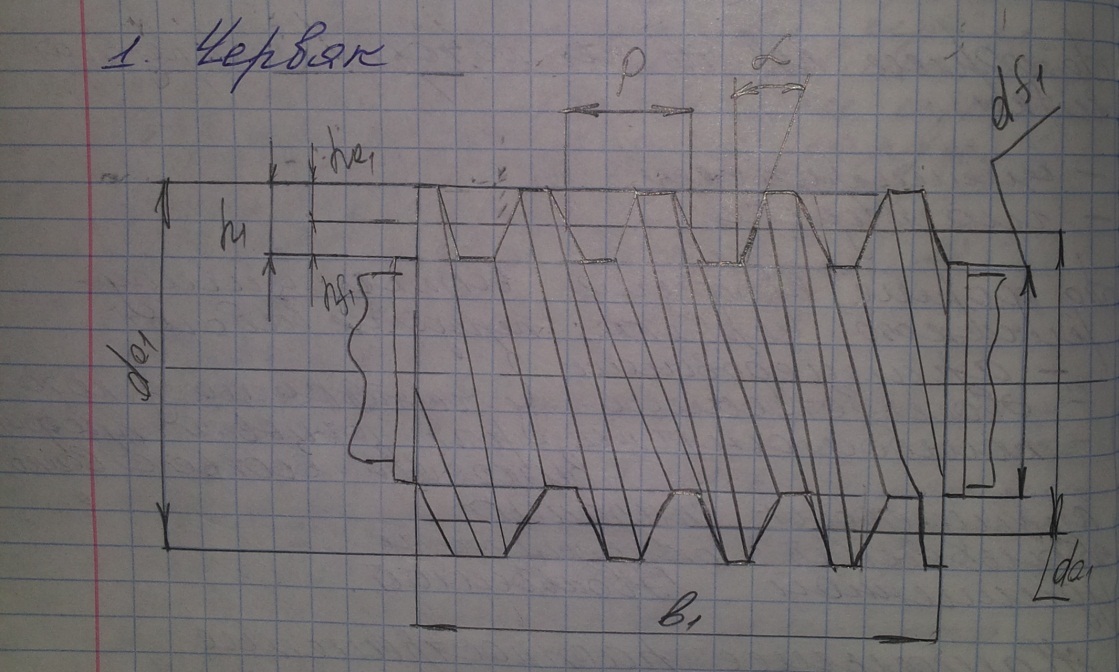
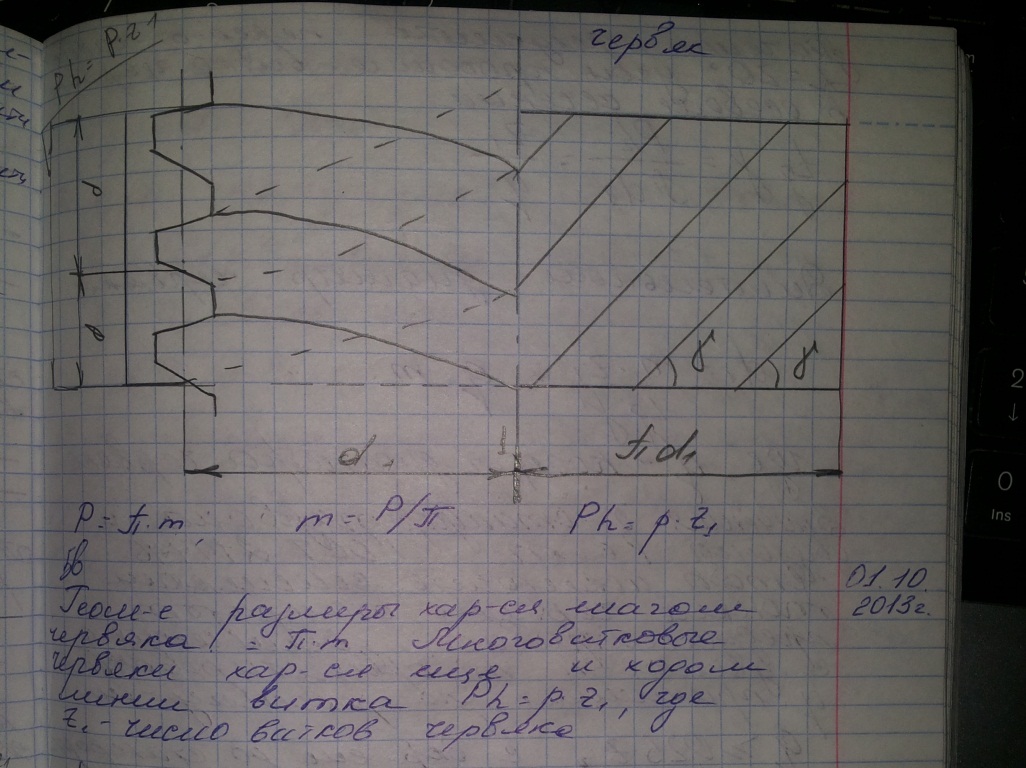
Шаг червяка: Р=π*m; где m= Р/ π;

Ход линии витка: Ph=p*z₁, где z₁- число витков червяка;

Угол профиля витка червяка в осевом сечении: α=20 градусов.

Угол подъема винтовой линии: tgγ=Ph/ π*d₁= z₁/q;

Делительный диаметр червяка: d₁=m* z₁/ tgγ= q*m, где q- коэффициент диаметра червяка;

q≥0,25*z₂ с округлением до стандартного значения.

Высота головки ножки витка червяка: ha₁=m; hf₁=1,2m; h=2,2m

Диаметр вершин и впадин витков червяка: da₁=d₁+2m; df₁=d₁-2,4m;

Длина нарезной части червяка: в₁=(C1+C2*z₂)*m, где С1 и С2- вспомогательные коэфф-ты.

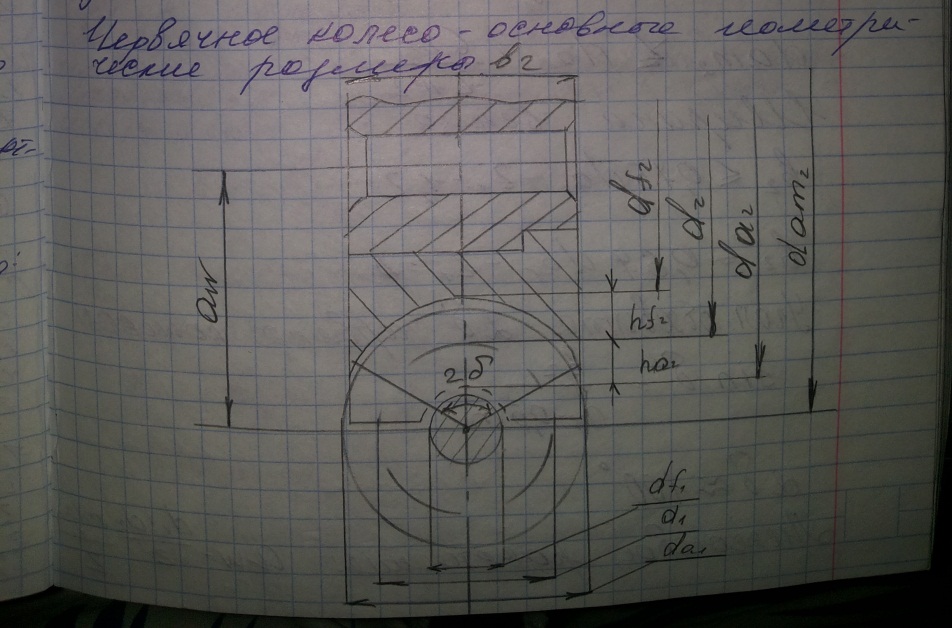
При заданном межосевом расстоянии коэффициент смещения равен:

χ=a_w/m – 0,5*(q +z₂ )

При смещении:

χ=a_w*0,5*m*(q+z₂+2x) z₂= 2a_w/m-q-2x

da₂= m(z₂+2+2x)

df₂=m(z₂-2,4-2x)

Другие размеры остаются неизменными. По условию неподрезания и незаострения зубьев, значение χ=[-1;+1]

Передаточное число:

U=n1/n2=w1/w2=z2/z1

Кинематические параметры червячной передачи

 В червячной передаче, в отличии от зубчатой, окружные скорости   и   не совпадают. Они направлены под углом 90⁰ и отличаются по значению. При относительном движении  начальные цилиндры скользят. При одном обороте червяка колесо поворачивается на угол,  охватывающий число зубьев колеса, равное числу заходов червяка.

 Основным преимуществом червячной передачи является большие передаточные отношения: в силовых передачах 10...80 , в кинематических передачах до  300 .

 При движении витки  червяка скользят по зубьям колеса, как в винтовой паре. Скорость скольжения  направлена по касательной к винтовой линии червяка

 Большое скольжение является причиной  снижения ККД, повышенного износа и заедания