51 Проектировочный расчет передач цилиндрическими зубчатыми колесами.

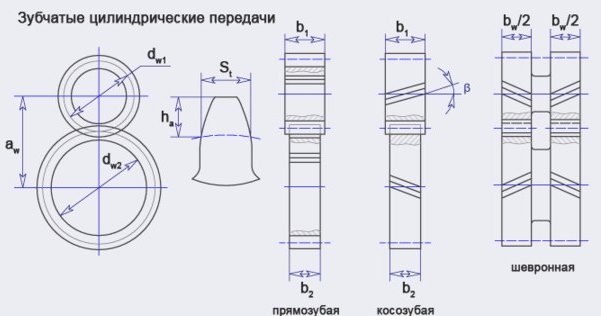
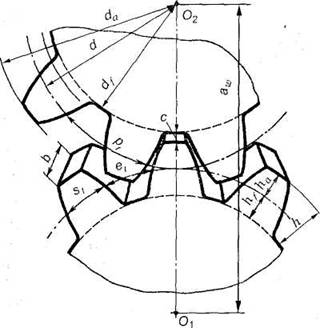
Параметр, обозначение	Расчетные формулы
Модуль т
Диаметр вершин зубьев da
Делительный диаметр d
Диаметр впадин зубьев df
Высота зуба h
Высота головки зуба ha
Высота ножки зуба hf
Окружная толщина зуба
Окружная толщина впадин зубьев
Радиальный зазор с
Межосевое расстояние
Окружной шаг рt
Длина зуба (ширина венца)

1. Определение ориентировочного значения межосевого расстояния

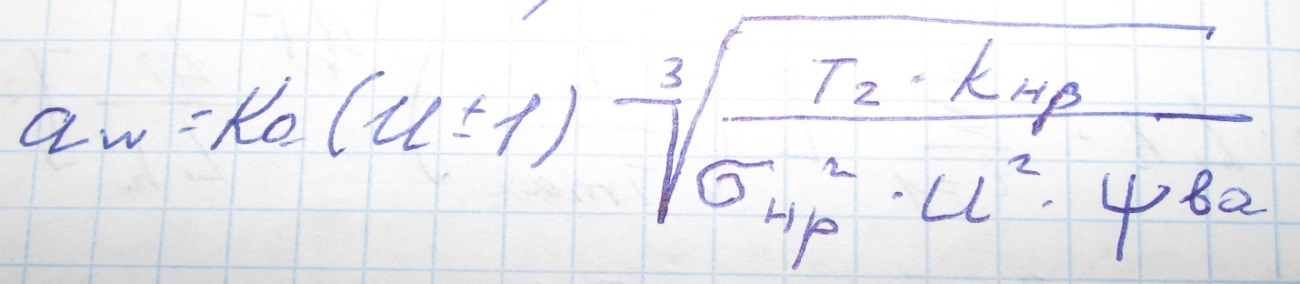
Где: Ка-вспомогательный коэффициент =495(прямозуб) 430 (косозуб и шеврон)

Т₂ –крутящий момент на колесе

U- передаточное число

К_HB –коэф-т учитывающий неравномерность распространения нагрузки по ширине венца, применяется в зависимости от параметра Ѱ_bd=b₂/d₁, Ѱ_bd=0,5 [Ѱ_ba (U±1)], Ѱ_ba=b₂/a_w.

Ѱ_bd – к-т ширины колеса относительно делительно делительного диаметра.

Ѱ_ba – к-т ширины колеса относительно межосевого расстояния, принимается в зависимости от положения колеса вз-ти опор. Межосевое расстояние применяют по ГОСТ 2185-66.

Нормальный модуль: M_n =(0.01…0.02)a_w.

Рабочая ширина колеса b₂= a_w* Ѱ_ba. . Ширина шестерни b₁=b₂+(5…7)мм.

Суммарное число зубьев Z_∑=2a_w/m-(прямозуб). Z_∑=2cosB* a_w/m( косозуб и шевронные.)

Число зубьев шестерни и колеса Z₁= Z_∑/(U+1), Z₂= Z_∑ - Z₁

Фактическое передаточное число Uф= Z₂/ Z_{1 ,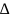} U =(U-Uф)/U*100%≤4%

Уточняем угол наклона зубьев: cosB=m(Z₁+Z₂)/2a_w

Определяем геометрические параметры зубчатых колес, прямозубые:d₁=m*Z_1,d₂₌ m*Z_2,

Косозубые d₁=m*Z₁/ cosB, d₂₌ m*Z₂/ cosB

Диаметр вершин колес da₁=d₁+2m, da₂₌ d₂+2m.

Диаметр впадин : df₁=d₁-2.5m df₂= d₂-2.5m

Проверяем межосевое расстояние a_w= d₁+ d₂/2.

Силы действующие в зацеплении: F_t=2T₂/d₂= F_t1, прямозуб:Fr= F_t*tgα,косозуб Fr= F_t*tgα/cosB.

Fa= F_t*tgB.

52 Расчет зубьев цилиндрических колес на сопротивление усталости при изгибе.

Проверочный расчет передачи на изгибную усталость. Расчетами определяется напряжение в опасном сечении на переходной поверхности зуба для каждого зубчатого зацепления.

1. Расчетное местное напряжение при изгибе σ_f= 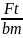*Kf*Yes*Y_β*Yε , где:

Kf-коэффициент нагрузки

Kf=Ka* Kfv*Kfβ*Kfα

Kfv-коэффициент, учитывающий динамическую нагрузку, возникающую до зоны резонанса

Kfv=1+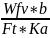 , где 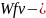удельная окружная динамическая сила , 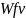=δ_f*ρ_0*v*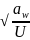

Где δ_f –коэффициент, учитывающий влияние вида зубчатой передачи и модификаций профиля головок зубьев.

Kfβ-коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий, принимают в зависимости от Ѱ_bd –по графику

Kfα- коэффициент, учитывающий распределение нагрузки между зубьями.

Yes- коэффициент, учитывающий форму зуба и концентрацию напряжения.

Для нахождения менее прочного звена необхадимо определить отношение σ_fp/ Yes- и проверку производить по тому из колес пары у которого это отношение меньше.

Y_β- коэффициент, учитывающий наклон зуба

Yε- коэффициент, учитывающий перекрытие зубьев , Yε=1 прямозубая, Yε=0,2+0,8/εα

Определяем эквивалентные числа зубьев шестерни и колеса

Zv₁=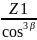 , Zv₂ = .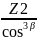