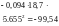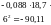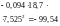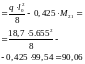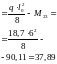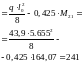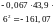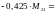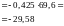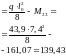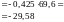2.3.3. Расчет по образованию трещин, нормальных к продольной оси.

Выполняем для выяснения необходимости проверки по раскрытию трещин. При этом для элемен­тов, к трещиностойкости которых предъявляют требова­ния 3-й категории, принимаем значения коэффициента надежности по нагрузке γ_f = 1;

М=63,6 кНм.

М<М_crc. Вычисляем момент образования трещин по приближенному способу ядровых моментов по формуле:

M_crc=R_bt,serW_pt+M_rp = 1,4∙3427,4(100) +2559 = 482395 Нсм - здесь ядровый момент усилия обжатия при γ_sp=1-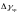 =1-0.3=0,7 составляет

M_rp= γ_sp P₂(e_0p+r) =0,7∙100360 (19,5+2,4) = 1538518,8 Нсм.

Поскольку М = 63600<M_crc=482395 , трещины в растянутой зоне не образуются. Следовательно, расчет по раскрытию трещин не требуется.

Проверяем, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэф­фициента точности натяжения = 1,13. Изгибающий момент от веса плиты М = 15,2кНм.

;

Расчетное условие

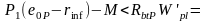
=1,13∙110824,7 (19.5-8,2)-1520000=1048794 Нсм;

1048794 <1589670 Нсм — условие удовлетворяется, на­чальные трещины не образуются; здесь

R_bp = 1 МПа — сопротивление бетона растяжению, соответствующее пе­редаточной прочности бетона R_bp =16 МПа (по прил. 2).

2.3.4. Расчет по раскрытию трещин, нормальных к продольной оси.

Расчет по раскрытию трещин, нормальных к продоль­ной оси при γ_sр =1. Предельная ширина раскрытия тре­щин: непродолжительная α_сrс=(0,3мм), продолжитель­ная α_crc=(0,9мм). Изгибающие моменты от нормативных нагрузок: постоянной и длительной М=34.71кНм; суммарной М=78.95кНм. Приращение напряжений в растянутой арматуре от действия посто­янной и длительной нагрузок по формуле:

α_s = [М — Р₂(z₁ - e_sp)]/W_s = (3471000 — 100360 ∙ 24,5]/34.1 (100) =296.8 МПа;

Здесь принимают z₁ =h₀ - 0,5h'_s=27 - 0,5∙5=24,5 см — плечо внутренней пары сил; e_sP = 0, так как усилие обжатия Р приложено в центре тяжести площади нижней напрягаемой арматуры: W_s = A_sz₁ = 1.39*24,5 = 34.1 см³— момент сопротивления сечения по растянутой арматуре.

Приращение напряжений в арматуре от действия пол­ной нагрузки

α_s = (6360000 — 100360∙24,5)/34.1(100) = 1144.04 МПа.

Вычисляем:

ширину раскрытия трещин от непродолжительного действия всей нагрузки

здесь 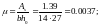d=12 мм - диаметр продольной арматуры;

ширину раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок

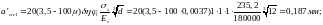
ширину раскрытия трещин от постоянной и длитель­ной нагрузок

Непродолжительная ширина раскрытия трещин

α_crc = α_crc1 – α’_crc1 + α_crc2 = 0,34 - 0,187 + 0,281 =0,394 мм<0,4 мм.

2.3.5. Расчет прогиба плиты.

Прогиб определяют от нормативного значения постоянной и длительных нагрузок; предельный прогиб составляет l₀/200=550/200=2.75см. Вычисляем параметры, необходимые для определения прогиба плиты с учетом трещин в растянутой зоне. Заменяющий момент равен изгибающему моменту от постоянной и длительной нагрузок М=34.71кНм; суммарная продольная сила равна усилию предварительного обжатия с учетом всех потерь и при γ=1; N_tot=P₂=100.36кН; эксцентриситет e_s,tot=M/ N_tot =3471 000/100360=34.6см; коэффициент φ_l =0,8 – при длительном действии нагрузки.

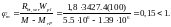
Коэффициент, характеризующий неравномерности деформаций растянутой арматуры на участке между трещинами, определяем по формуле:

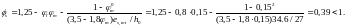
Вычисляем кривизну оси при изгибе по формуле:

Здесь, А_b=146∙5=980см²

Вычисляем прогиб по формуле:

2.4. Расчет ригеля в составе рамы с учетом перераспределения напряжений.

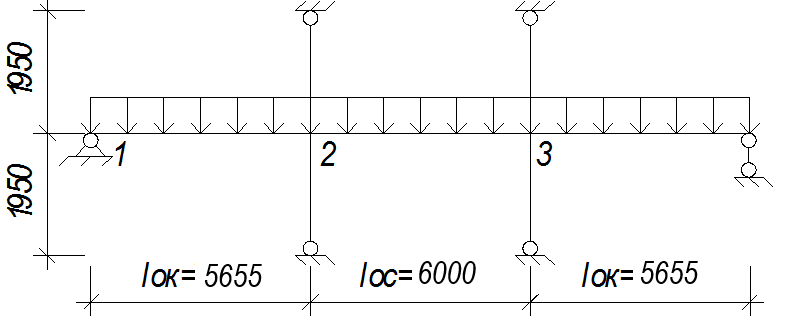
2.4.1. Расчетные схемы и нагрузки.

Расчетные пролеты неразрезного ригеля назначаются равными расстоянию между осями колонн, а в крайнем пролете при опирании одним концом на кирпичную стену- расстоянию от оси колонны до середины площадки опирания ригеля на стену.

Крайние пролеты:

, где 510 мм-длина площадки опирания ригеля.

Средние пролеты:

С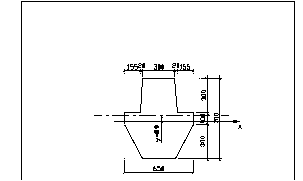 обственная масса ригеля вычисляется по предварительно принятым размерам сечения

Рис. 7

Подсчет нагрузок на 1м² перекрытия приведен в таблице 6.

Таблица 6.

N	Вид нагрузки	Нормативная нагрузка кН/м		Коэффициент γf		Расчетная нагрузка
1	2	3		4		5
	Постоянная:
1	Собственный вес плиты	1,72		1,1		1,892
2	Конструкция пола	0,439				2,55
	Итого	2,159				4,442
4	Временная нагрузка	7,9		1,2		9,48
Всего:			10,519				13,92

2.4.2. Определение усилий в ригеле.

1)Определим погонную нагрузку на ригель.

Нагрузка на ригель от ребристых плит является сосредоточенной, но при числе ребер в пролете более четырех принимается равномерно распределенной. Ширина грузовой полосы на ригель равна шагу поперечных рам– 5,5 м.

Нагрузка, передаваемая каждым ребром:

G=4,442·1,6·5,5=20,18 кН.

V=9,48·1,6·5,5=83,47 кН.

Заменим сосредоточенные нагрузки эквивалентными равномерно распределенными [стр.18, 11]:

.

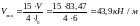
А риг=0,5*2*30*2+30*70+17,5*2*10+0,5*17,5*2*30=3035 см².

Собственный вес 1 погонного метра ригеля: g риг=3035·10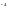 ·1·25·1,1·0,95=7,9 кН/м.

Итого: g= ,

V=43,9 кН/м.

2) Вычислим изгибающие моменты в расчетных сечениях ригеля.

Длина колонны 3,8 м, сечение 40х40 см.

Отношение погонных жесткостей ригеля и колонны:

,

где B,l-жесткость и пролет ригеля;

Bcol, lcol-жесткость и длина колонны.

Определим момент инерции для ригеля:

Sриг=0,5*2*30*2*15++17,5*2*30*0,5*15=8775 см³,

y=Sриг/А риг=8775/3035=2,9 см,

Iриг=30*70*2,9²+30*70³/12+2*(0,5*30*2*12,1²+2*30³/36+17,5*10*2,9²+17,5*10³/12+0,5*17,5*30*

*17,9²+17,5*30³/36)=1087271 см³.

Iкол=40*40³/12=213333 см³.

С учетом различной длины для крайних и среднего пролетов значение коэффициента k составляют:

;

Определим опорные моменты в ригеле при различных схемах загружения, результаты сведены в таблицу 7.

Таблица 7

Схема загружения	Опорные моменты, кНм
	М21	М23		М32			М34
1
Пролетные моменты, кНм	М1=		М2=		М3=
2
Пролетные моменты, кНм	М1=		М2=-50,48			М3=
3
Пролетные моменты, кНм	М1=		М2=			М3=
4
Пролетные моменты, кНм	М1=		М2=			М3

2) Составим сочетание различных схем загружения.

Значение опорных и пролетных моментов ригеля при различных сочетаниях схем загружения приведены в таблице 8.

Таблица 8

Сочетание схем загружения	Изгибающие моменты, кНм
	опорные				пролетные
	М21	М23	М32	М34	М1	М2	М3
1+2	-263,61	-140,59	-140,59	-263,61	331,06	-12,59	331,06
1+3	-203,86	-242,55	-242,55	-203,86	45,72	185,95	45,72
1+4	-360,56	-328,1	-224,73	-234,16	289,86	145,11	32,85

3) Поперечные силы:

Схема загружения 1+2

;

;

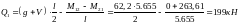Схема загружения 1+3

;

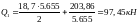
Схема загружения 1+4:

;

.

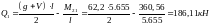4) Перераспределение изгибающих моментов под влиянием образования пластических шарниров в ригеле.

Наибольший опорный момент возникает на опоре 2 при загружении по схеме 1+4,

Мmax=360,56 кНм, уменьшим его на 30%: после перераспределения ордината опорного момента

,

такое же значение сохраним и для опорного изгибающего момента М23=-252,39 кНм.

Ординаты дополнительной выравнивающей эпюры моментов составят:

;

;

.

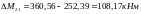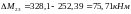Ордината опорного момента М21 для упругой стадии работы по схеме 1+2 превышает значение соответствующего перераспределенного момента по схеме загружения 1+4, поэтому добавлением дополнительной эпюры к схеме загружении 1+2 устанавливаем величину изгибающего момента

Ординаты дополнительной выравнивающей эпюры моментов составят:

;

;

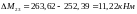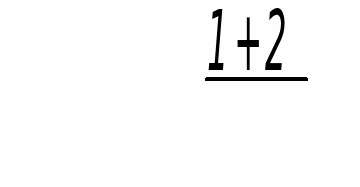
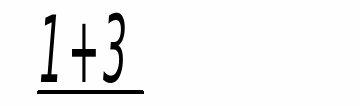
5) Выполним сравнительный анализ величин граневых опорных изгибающих моментов. При этом необходимо выявить наибольший (расчетный) изгибающий момент, действующий по грани промежуточной опоры (колонны) слева и справа.

Изгибающий опорный момент по грани опоры 2 слева:

• Схема загружения 1+2

Поперечные силы с учетом перераспределения изгибающих моментов:

.

;

Момент по грани колонн:

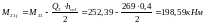
• Схема загружения 1+3

,

.

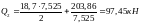• Схема загружения 1+4

.

;

Момент по грани колонн:

Опорные изгибающие моменты по грани опоры 2 справа:

• Схема загружения 1+2

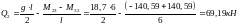
(вторая промежуточная опора слева).

(на 2-ой промежуточной опоре слева).

• Схема загружения 1+3

;

;

.

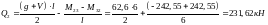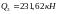• Схема загружения 1+4

;

.

.

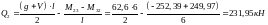Из проведенного анализа видно, что расчетный граневой момент на промежуточных опорах равен 206 кНм.

6) Установим значение поперечных сил для расчета прочности наклонных сечений на крайних и промежуточных опорах. Их значение принимаются наибольшими из двух расчетов: упругого и с учетом перераспределения моментов. С этой целью определим значение поперечных сил для схемы загружения 1+4, рассматривая ригель как упругую систему.

На крайней опоре

;

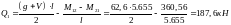на второй опоре слева ;

на второй опоре справа ;

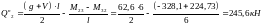на третьей опоре слева .

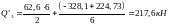Из сравнительного анализа значений поперечных сил по пунктам 3, 5, 6, получим наибольшие их значение на опорах:

а) крайней ;

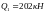б) №2 слева ;

в) №2 справа .

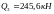2.4.3. Расчет прочности ригеля по сечениям нормальным к продольной оси.

Характеристики прочности бетона и арматуры. Бетон тяжелый класса В20; расчетные сопротивления при сжа­тии R_b = 11,5 МПа: при растяжении R_bt=0,9 МПа; ко­эффициент условий работы бетона γ2=0,90; модуль уп­ругости Еb = 24000МПа.

Арматура продольная рабочая класса A-III, расчетное сопротивление R_s=365 МПа, модуль упругости E_s = 200000 МПа, R_sw=290 МПа.

Определение высоты сечения ригеля.

Высоту сечения подбираем по максимальному граневому моменту. Принятое сечение ригеля следует затем проверить по пролетному моменту (если он больше опорного) так, чтобы относительная высота сжа­той зоны была ξ<ξ_R.

Высота сечения при ξ=0,35, αm=0,289

Вычисляем:

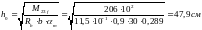
h = h₀+a = 47,9+5 = 52,9см; принимаем h=70 см.

h₀=70-5=65 см.

Определим граничную относительную высоту сжатой зоны:

,

где ,

, .

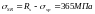Проверим принятое сечение по пролетному моменту

Вычислим

,

;

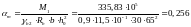Требуемое количество арматуры для армирования ригелей крайних пролетов:

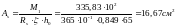
Принимаем 425 A-III с А_s = 19,63 см²

В среднем пролете: ,

,

,

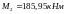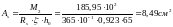
Принимаем 418 A- III с А_s = 10,18см².

Арматуру для восприятия отрицательного момента в пролете устанавливаем по эпюре моментов. Принимаем 212A- III с А_s = 2,26 см².

В сечениях на промежуточных опорах наибольший граневой момент

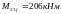
Арматуру для восприятия этого момента располагаем в один ряд.

Тогда ;

;

;

;

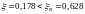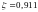На верху уже есть 212A- III с А_s = 2,26 см², поэтому Аs =9,68-2,26=4,72 см²

Принимаем 222 A- III с А_s = 7,6 см².