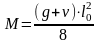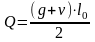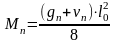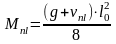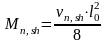- •Содержание
- •Расчёт плиты опёртой по контуру
- •1.3.Расчёт арматуры плит
- •2. Расчёт балок при плитах, опёртых по контуру
- •2.1 Расчётные пролёты и нагрузки
- •2.2 Определение усилий
- •2.3 Расчёт сечения продольной арматуры.
- •2.4 Расчёт прочности балки б-1 по сечениям, наклонным к продольной оси.
- •3. Расчёт простенка наружной стены здания
- •4. Расчёт армокаменного столба
- •2.3.3. Расчет по образованию трещин, нормальных к продольной оси.
- •2.3.4. Расчет по раскрытию трещин, нормальных к продольной оси.
- •2.4.4. Расчет прочности ригеля по сечениям наклонным к продольной оси.
- •2.4.5. Конструирование арматуры ригеля.
4. Расчёт армокаменного столба
Определим расчётную нагрузку на столб подвала трёхэтажного здания. Высота подвала Нподв = 3,6 м.
Грузовая площадь
на столб
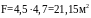 .
.
Нагрузки на 1 м2 покрытия и перекрытия, кН/ м2
Таблица 6
Нагрузка |
Покрытие, кН/м2 |
Перекрытие, кН/м2 |
Постоянная |
8,2 |
5,86 |
Временная |
1,8 |
9,48 |
Временная длительно действующая |
1,85 |
1,68 |
полная qпок |
10,00 |
15,34 |
полная длит. действ qд.пок |
10,05 |
7,54 |
Нагрузка на столб подвала без учёта его собственной массы:
 .
.
Собственная масса столба может быть принята 5% от полной расчётной нагрузки:
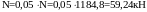 .
.
Полная расчётная нагрузка с учётом массы столба
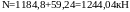 .
.
Принимаем кладку из кирпича СУР-125/35 на растворе марки 50. Расчётное сопротивление сжатию R=1,7МПа. Упругая характеристика α=750. В качестве арматурных сеток используем проволоку класса Вр-I диаметром 4мм, расчётное сопротивление которой в кладке Rs=219МПа, нормативное Rsn=243 МПа, Аst=0,126см2.
Принимаем Rsk=2∙R=3,4МПа – максимально возможное значение расчётного сопротивления армированной (сетками) кладки сжатию.
Определим необходимый процент армирования, обеспечивающий заданную прочность Rsk кладки:
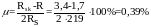 ,
,
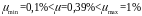
Принимая сетки с квадратной ячейкой размером с=40мм, определим их необходимый шаг S по высоте кладки:
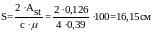 .
.
Выражаем полученное значение S через эквивалентное число рядов кладки из кирпича СУР-125/35 толщиной 6,5см.
n=16,15/6,5=2,48
Устанавливаем сетки с шагом S, равному двум рядам кладки.
Вычислим упругую характеристику кладки с сетчатой арматурой и временные сопротивления неармированной Ru и армированной кладки Rs кл.
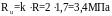 ;
;
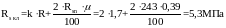 ;
;
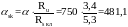 .
.
Используя
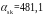 по таблице принимаем φ = 0,98, при этом λh
= 4.
по таблице принимаем φ = 0,98, при этом λh
= 4.
При гибкости λh = 4 η =0 и mg = 1.
Определяем в первом приближении площадь и размеры поперечного сечения армированного столба:
 ;
;
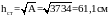 .
.
Исходя из размеров стандартного кирпича и наличия швов принимаем h=64см.
Определим расхождение
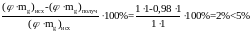
Проверим достаточность принятых размеров сечения:
 .
.
5. РАСЧЁТ КАМЕННОГО ФУНДАМЕНТА ПОД ЦЕНТРАЛЬНО-НАГРУЖЕННЫЙ СТОЛБ
Фундамент запроектирован из бутобетона. Марка бутового камня 100, марка бетона 50. Расчётное сопротивление сжатию бутобетона Rб = 1,6 МПа. Расчетное сопротивление грунта R = 0,31 МПа.
Полная расчётная нагрузка с учётом собственного веса столба:
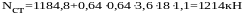
Расчётная нагрузка в уровне верхнего обреза фундамента:
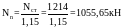
Полная собственная масса фундамента приблизительно равна 10% от Nn, вычислим размер его подошвы:
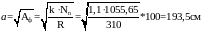 .
.
Принимаем а=200см. При этом давление на грунт при расчётной нагрузке составит:
 ,
,
получаем k = 1,25. Высота фундамента составит:
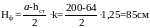 ,
,
принимаем
 .
.
Высоту нижнего участка фундамента принимаем 25см, двух верхних – 30 см. Размер вылета нижнего уступа принимаем - 20,5 см и верхнего – 22см. Размер стороны верхнего обреза фундамента составит 95см.
Проверим прочность фундамента на местное сжатие под подошвой армокаменного столба, т.е. условие Nсм>N:
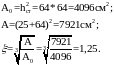
Принимаем
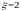 :
:

Прочность фундамента на местное сжатие обеспечена.
2. Сборное перекрытие.
2.1. Компоновка сборного варианта.
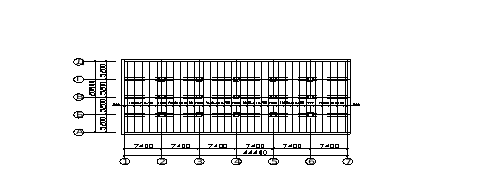
2.2. Расчет предварительно напряженной ребристой плиты по предельным состояниям I группы.
Исходные данные: размер плиты в плане 5650х1500мм. Принимаем для изготовления бетон класса В30 [п. 2.6., 8], Rв = 17 МПа; RBt = 1,2 МПа; RB,ser = 22 МПа; RBt.ser = 1,8 МПа. Начальный модуль упругости бетона, при естественном твердении Еb =32500МПа. Коэффициент условия работы бетона γb2 = 0,9.
Напрягаемая арматура продольных ребер плиты принята К-7 с расчетным сопротивлением Rs = =1100 МПа; Rs,ser = 1335 МПа, Es=180000 МПа.
Изделие изготавливается по поточно-агрегатной технологии, натяжение арматуры производиться на упоры формы электротермическим способом.
.
2.2.1 Определение расчетного пролета плиты и сбор нагрузок.
Расчетный пролет плиты принимается равным расстоянию между серединами площадок опирания плиты на консоли ригеля.
l0= l-b/2=5,65–0,3/2=5,5м.
Lcon=L-b=5,65-0,3=5,35м.
Подсчет нагрузок на 1м2 перекрытия приведен в таблице 4.
Таблица 4
№ п/п |
Наименование нагрузок |
Нормативная нагрузка, кН/м2 |
γf |
Расчетная нагрузка, кН/м2 |
I |
Постоянная нагрузка |
|
|
|
1 |
Плиточный пол, δ=15мм, ρ=1800кг/м3 |
0,27 |
1,2 |
0,32 |
2 |
Цементная стяжка δ=20мм, ρ=2200кг/м3 |
0,44 |
1,3 |
0,57 |
3 |
Шлакобетон, δ=80мм, ρ=1600кг/м3 |
1,28 |
1,3 |
1,66 |
4 |
Плита перекрытия |
1,72 |
1,1 |
1,89 |
|
ИТОГО |
3,71 |
|
4,44 |
II |
Временная (полезная) в т.ч: |
7,9 |
1,2 |
9,48 |
|
Длительная |
1,4 |
1,2 |
1,68 |
|
Кратковременная |
6,5 |
1,2 |
7,8 |
|
ИТОГО |
11,61 |
|
13,92 |
Полная нормативная нагрузка плиты при ширине 1,5 м:
gп+vп=11,61·1,5=17,42кН/м.
Полная расчетная нагрузка: g+v=13,92·1,5=20,88 кН/м.
Постоянная + длительная нагрузка: g+vnl=(4,44+1,68)·1,5=9,18 кН/м.
Кратковременно действующая нагрузка: Vnsh =7,8*1,5=11,7 кН/м.
2.2.2. Усилия от расчетных и нормативных нагрузок.
Расчет усилий в плите приведен в таблице 5.
Таблица 5
№ |
Вид нагрузки |
Формула подсчета |
Величина усилия (кНм, кН) |
1 |
Полная расчетная |
|
20,88·5,52/8=78,95 |
2 |
Полная расчетная |
|
20,88·5,5/2=57,42 |
3 |
Полная нормативная |
|
17,42·5,52/8=65,87 |
4 |
Постоянная + длительная |
|
9.18·5.52/8=34.71 |
5 |
Кратковременная |
|
11.7·5.52/8=44.24 |
2.2.3. Компоновка поперечного сечения плиты.
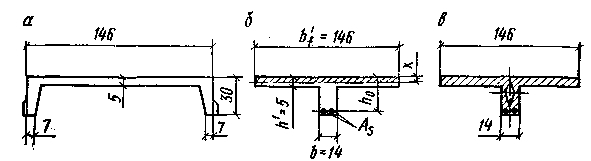
Рис.4 Поперечные сечения ребристой плиты
а – основные размеры, б – к расчету прочности, в – к расчету по образованию трещин
Высоту сечения ребристых предварительно напряженных плит можно предварительно назначить равной:
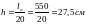 ;
принимаем h=30
см, тогда рабочая (полезная) высота
сечения равна ho
= h
– a
= 30 – 3 = 27 см.
;
принимаем h=30
см, тогда рабочая (полезная) высота
сечения равна ho
= h
– a
= 30 – 3 = 27 см.
Ширину продольных ребер понизу принимаем 7см, а ширину плиты поверху 150-4=146 см, толщину полки – 5 см. Фактическое П-образное сечение плиты приводится к эквивалентному тавровому сечению.
При отношении
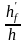 = 5/30 = 0,167 > 0,1 принимаем bf’
= 146 см.
= 5/30 = 0,167 > 0,1 принимаем bf’
= 146 см.
Расчетная ширина ребра эквивалентного таврового сечения b=2∙7=14см.
2.2.4. Расчет прочности плиты по сечениям, нормальным к продольной оси
Определим положение нейтральной оси.
Коэффициент статического момента сжатой зоны бетона считается по формуле:

По таблице найдем: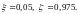
 <5
см – толщины полки.
<5
см – толщины полки.
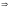 нейтральная
ось проходит в пределах сжатой полки.
нейтральная
ось проходит в пределах сжатой полки.
Вычислим граничную относительную высоту сжатой зоны:
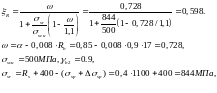
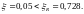
Определим коэффициент, учитывающий работу высокопрочной арматуры при напряжениях выше условного предела текучести.
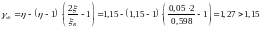 ,
,
где η=1,15 , для
арматуры К-7. Принимаем
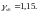
Определим требуемую площадь сечения растянутой напрягаемой арматуры:

Принимаем 212 К-7, Asp=2,26см2
2.2.5. Расчет полки на местный изгиб.
Полку плиты армируем сеткой из арматурной проволоки Вр-1.
Расчетный пролет при ширине ребер вверху 9 см составит l0=146–9∙2=128 см.
Нагрузка на полку(погонная нагрузка на плиту за вычетом 1 погонного веса ребер ):
(gn+ Vn) = 13,92 -2∙0,3∙0,08∙25=12,72кН/м
Изгибающий момент для полки шириной 1м: М=12,72·1,282/11 = 1,89 кН·м.
Рабочая высота сечения h0=5–1,5=3,5см (1,5см – защитный слой).
Коэффициент статического момента сжатой зоны бетона:
αm
=
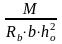 =
=
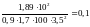 ;
;
ζ = 0,945;
AS
=
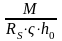 =
=
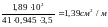 .
.
По конструктивным требованиям расстояние между осями рабочих стержней при толщине плиты до 150 мм должно быть не более 200мм. Принимаем сетку с поперечной рабочей арматурой Æ5 класса Вр-1 с шагом S=150 и распределительной продольной арматурой Æ5 Вр-1 с S=200 мм.
2.3.3. Расчет прочности плиты по сечению наклонному к продольной оси.
Максимальная поперечная сила от полной расчетной нагрузки Qmax=57,42 кН.
Проверим необходимость постановки поперечной арматуры по расчету. Поперечная арматура не требуется, если выполняется условие:


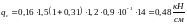 ;
;
Т.к.
 =
=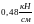 >0,092
>0,092
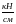 , то с=с
, то с=с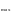
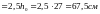
 ;
;
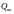 считается по
формуле
считается по
формуле
 ;
;
 ,
следовательно поперечную арматуру
необходимо подбирать по расчету.
,
следовательно поперечную арматуру
необходимо подбирать по расчету.
В ребристых плитах диаметр поперечного сечения обычно не превышает 4-6мм. На приопорном участке длинной 1/4l в каждом продольном ребре устанавливаются поперечные стержни диаметром 5мм класса Вр-1 с шагом S1=150мм, в средней части пролета с шагом S2 = 250мм.
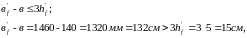 ,
,
принимаем
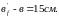
 ;
;
Коэффициент к=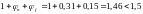 ;
;
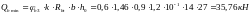

Проверим условие:
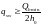 ;
;
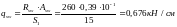 ;
;
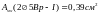 ;
;
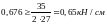 - условие выполняется.
- условие выполняется.
Проверим требование

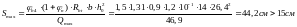 - требование
выполняется.
- требование
выполняется.
Несущая способность расчетного наклонного сечения по поперечной силе:
Для расчета
прочности вычислим момент
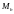 :
:
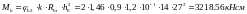 ;
;
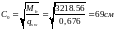
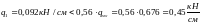

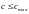

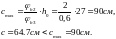
– условие выполняется.
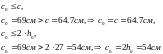

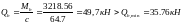 ;
;

Поперечная сила в конце наклонного расчетного сечения:
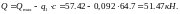
Условие прочности:
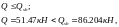
Следовательно прочность плиты по наклонному сечению обеспечена.
2.3. Расчет предварительно напряженной ребристой плиты по предельным состояниям 2 группы.
2.3.1. Определение геометрических характеристик приведенного сечения.
Отношение модулей упругости α=Es/Eb=180000/29000=6,21. Площадь приведенного сечения Aгеd =A+αAs=146∙5+14∙25+6,21∙1,39=1088,6см2. Статический момент площади приведенного сечения относительной нижней грани Sred=146∙5∙27,5+14∙25∙12,5+6,21∙1,39∙3=24476 см3. Расстояние от нижней грани до центра тяжести приведенного сечения
yо = Sred/Ared =24476/1088,6 = 22,5 см.
Момент инерции
Ired= 128∙53/12+128∙5∙5,52+14∙303/12+14∙30∙72+6,21∙1,39∙202=44067 см4.
Момент сопротивления приведенного сечения по нижней зоне
Wred =Ired/y0 =44067/22,5=1958,5 см3.
Момент сопротивления приведенного сечения по верхней зоне
W’red =Ired/(h0 – y0)= 44067/(30 – 22,5) = 5,875,6 см3
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней) до центра тяжести приведенного сечения, r=φWred/ /Aгеd=0,85∙1958,5/1088,6 = 1,53 см; то же, наименее удаленной от растянутой зоны (нижней) rinf = 0,85∙5875,6/1088,6 = 4,6 см; здесь φ=1,6—σbp/Rb.ser 1,6—0,75 = 0,85.
Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимают равным 0,75.
Упругопластический момент сопротивления по растянутой зоне,
WPl=γWred = 1,75∙1958,5 = 3427,4 см3; здесь γ = 1,75 — для таврового сечения с полкой в сжатой зоне.
Упругопластический момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента WРl = 1,5∙5875,6=8813,4 cм3; здесь у = 1,5 — для таврового сечения с полкой в растянутой зоне при bf/b>2 и hf/h<0,2.
2.3.2. Определение потерь предварительного напряжения в арматуре.
Потери от релаксации напряжений в арматуре при электротермическом способе натяжения σ1 =0,03σsр = 0,03∙822 = 24,66 МПа.
σsр=0,6 Rsn=0,6*1370=822МПа
Потери от температурного перепада между натянутой арматурой и упорами σ2=0, так как при пропаривании форма с упорами нагревается вместе с изделием.
Усилие обжатия P1=As(σsp-σ1)=1,39(822—24,7)∙(100)=110824,7 Н. Эксцентриситет этого усилия относительно центра тяжести приведенного сечения еор = = у0 — а = 22,5 — 3=19,5 см. Напряжение в бетоне при обжатии:
σbp=Pl/Ared+Р1∙е0Py0/Ired =
= (110824,7/1088+110824,7∙19,5*22,5/44067)/100 = 1,21 МПа.
Устанавливают передаточную прочность бетона из условия σbp/Rbp;
1,21/24=0,05 МПа<0,5В30; принимают Rbp= 0,8∙30 =24МПа. Тогда σbр/Rbp = 0,8.
Вычисляем сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия Р1 и с учетом изгибающего момента от веса плиты
М =2490∙2∙5,52/8=18,8 кНм. Тогда
Потери от быстронатекающей ползучести при σbр/Rbp = 0,05 и при α<0,8 составляют
σ6 =40∙0,85∙ σbp/Rbp= 0,85∙40∙0,05=1,62МПа.
Первые потери σlos1=σ1+σ6=24,7+1,62=26,32 МПа.
С учетом потерь σlos1 напряжение σsp1=σsp–σ1–σ6 =822 – 26,32=795,7МПа,
Р1= σsp1∙Аsp=795,7∙1,39∙100=110602,3Н.
σbp1 = P1/Ared + (P1 e0p — М) eop/Ired =
= [110824,7/1088 + (110824,7∙19,5 — 17,5∙19,5∙100000)/44067] 1/100 = 2,74 МПа
Потери от осадки бетона σ8=35 МПа. Потери от ползучести бетона при
σbp/Rbp=2,74/24=0,11 составляют σ9=150∙0,85∙0,11=14,03МПа.
Вторые потери σlos2=σ8+σ9=35+14,03 =49,03 МПа.
Полные потери σlos=σlos1+σlos2=26,32+49,03=75,35<100МПа, т.е. больше установленного минимального значения потерь. Принимаем σlos=100
Усилие обжатия с учетом полных потерь Р2=Аs(σsp— σlos) =1,39(822— 100)∙(100) = 100,36 кН.