2. Расчёт балок при плитах, опёртых по контуру

Рис. 2. Нагрузки на балки.

В перекрытии имеются неразрезные балки двух видов: девятипролетные балки Б-1 и девятипролетные балки Б-2. Сечени е при расчете плит принято одинаковое bхh=20х50. Нагрузки на балки передаются с плит по площадям, ограниченным биссектрисами углов их контура, т.е. с меньшего пролёта по закону треугольника, а с большего – по трапеции. Расчётные схемы балок приведены на рис. 2.

Расчёт балки Б-1 проводим как обычный неразрезной девятипролетной балки с учётом перераспределения усилий на действие нагрузки, распределённой по трапеции.

2.1 Расчётные пролёты и нагрузки

Крайние расчётные пролёты балок Б-1:

,

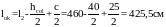где h_col= 40см – размер сечения колонны; с = 25см – глубина заделки балки в стену. Средний расчётный пролёт принимается равным расстоянию h света между колоннами:

.

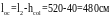Расчётная (погонная) равномерно распределённая нагрузка от собственной массы балки и части конструкции перекрытия, непосредственно расположенной над балкой шириной b=20см:

,

то же маленькая нагрузка, расположенная непосредственно над балкой:

.

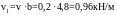Суммарная равномерно распределённая нагрузка над балкой

.

Постоянная расчётная погонная (распределённая по закону треугольника и трапеции) нагрузка, действующая на балку от собственной массы конструкции перекрытия с двух прилегающих к балке плит:

Расчётная погонная временная нагрузка, действующая на балку по закону треугольника и трапеции

Эквивалентная равномерно распределённая нагрузка, передаваемая на балку:

постоянная

временная

Суммарная постоянная равномерно распределённая нагрузка:

Суммарная временная равномерно распределённая нагрузка

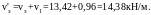
2.2 Определение усилий

Изгибающие моменты в свободно опёртых однопролётных балках при действии нагрузки по площади трапеции с двух смежных плит:

.

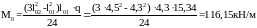где

Изгибающие моменты в крайних пролётах и первой промежуточной опоре:

.

Изгибающий момент в среднем пролёте:

.

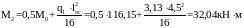Поперечные силы на опорах:

на крайней опоре

на первой промежуточной опоре слева:

на первой промежуточной опоре справа:

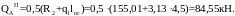
Для построения огибающей опоры изгибающих моментов балки Б-1 вычислим минимальные значения пролётных моментов. С учётом эквивалентных нагрузок расчётные равномерно распределённые нагрузки на балку будут равны:

:

Расчётные минимальные моменты в пролётах равны:

в крайних пролётах

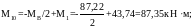
в средних пролётах:

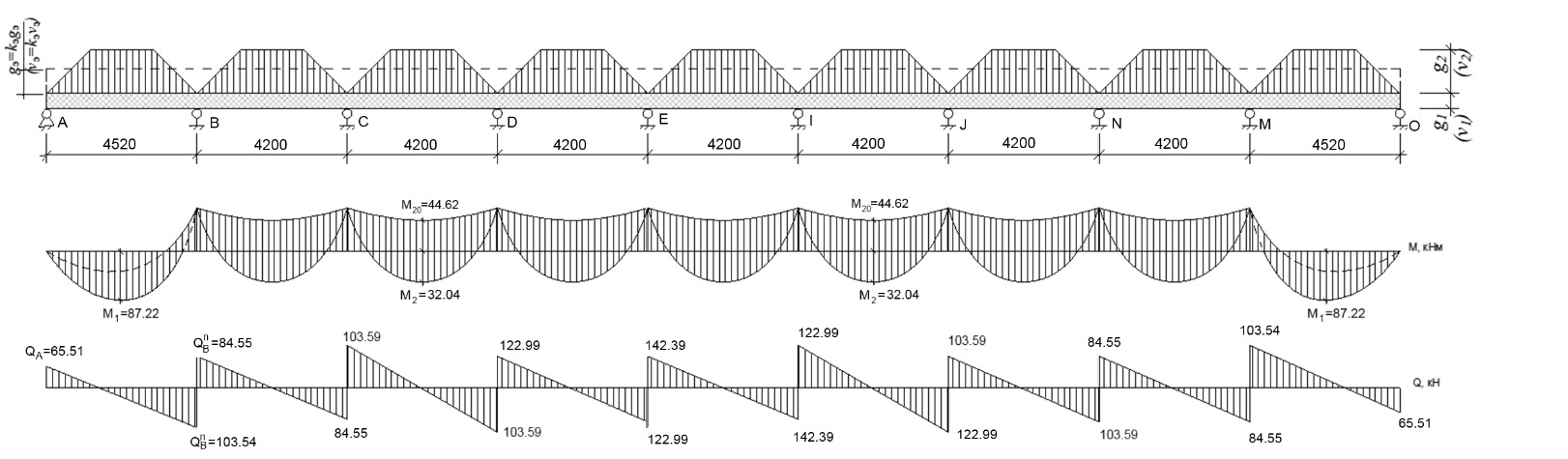
Рис. 3. Схема нагружения балок Б-1 и эпюры M и Q

2.3 Расчёт сечения продольной арматуры.

В начале уточним высоту сечения балки по опорному моменту, принимая ξ=0,35 и соответственно α_m = 0,289. Тогда

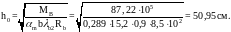
Окончательно принимаем балку сечением 20х55см. h₀ = 55–4=51 см. Сечение балки является тавровым с полкой в сжатой зоне. Отношение Вводимая в расчет ширина сжатой полки должна быть не менее

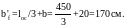
Принимаем (толщина плиты).

Определим положение нейтральной оси. Момент, воспринимаемый полкой сечения:

Следовательно, нейтральная ось проходит в полке. Расчёт ведём как элементов прямоугольного сечения шириной .

Для крайнего пролёта вычислим α_m:

.

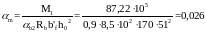По таблице 3.1 [3] определяем ξ = 0,03, ζ = 0,985. Полученное ξ = 0,03<0,65.

Граничное значение относительно высоты сжатой зоны

.

Где , т.к. диаметр арматуры балки более 10мм. Остальные характеристики в формуле такие же как и при вычислении для плит.

Требуемую площадь сечения арматуры определим по формуле:

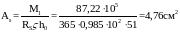
Принимаем 2 18 А-III с А_S=5,09 см². Процент армирования при одной сетке:

.

Для среднего пролёта вычислим α_m:

,

тогда ξ = 0,01, ζ = 0,995. Полученное ξ = 0,01<0,947.

Требуемую площадь сечения арматуры определим по формуле:

Принимаем 2 12 А-III с А_S=2,26см². Процент армирования при одной сетке:

.

Вычислим α_m для первой промежуточной опоры:

,

тогда ξ = 0,25, ζ = 0,875. Полученное ξ = 0,25<0,65.

Требуемую площадь сечения арматуры определим по формуле:

Принимаем 2 20 А-III с А_S=6,28см². Процент армирования при одной сетке:

.

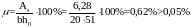Вычислим α_m в верхней зоне среднего пролёта балки:

,

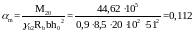тогда ξ = 0,12, ζ = 0,94.

Требуемую площадь сечения арматуры определим по формуле:

Принимаем 2 14 А-III с А_S=3,08см². Процент армирования при одной сетке:

.
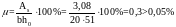