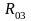Теория машин и механизмов
0,4Н
w

Схема исполнительного механизма
График силы полезного сопротивления

А

d
Исходные данные:
lAB = 0.06 m,
LBC = 0.15 m,
d = 60 mm,
P = 1,8 МПа,
ω = 18c-1
Структурный анализ механизма.
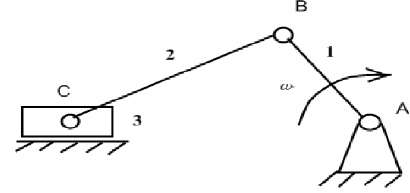
Рисунок 1. Структурная схема механизма
Механизм является кривошипно-ползунным. В его состав входят: Кривошип 1, шатун 2, ползун 3. Количество кинематических пар равно четырем. Определяем степень подвижности механизма по формуле Чебышева.
W= 3n -2P1–P2
W= 3∙3 – 2∙4 = 1
Из четырех кинематических пар три вращательных ( В01 ,В12, В23 ) и одна поступательная П03. Выделим из механизма группу Ассура.
Ведущим звеном является кривошип. Группа Ассура имеет следующий вид: [ В12 - В23 - П30] Таким образом, строение механизма выражается формулой
В01 →[В12 - В23 - П30]
Исследуем механизм на наличие избыточных связей. q= W- 3 n+ 2P1
q= 1 - 9 + 8 = 0 Избыточных связей нет.
Кинематический анализ механизма.
Построение планов положений механизма.
Для решения задачи кинематики построим механизм в восьми равностоящих друг от друга положений механизма начиная от крайних. Пусть на чертеже АВ=36 мм, тогда масштаб длины:
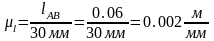

На чертеже окружность поделена на 8 равных частей, в сторону рабочего хода. Рассчитаем силу сопротивления.
Fc = PS = 1,8·3.14·302=5086,8 Н
Построим график изменения силы сопротивления, выбираем масштаб: ПустьFmax= 100мм, тогда:

Определим величину действующей силы во всех положениях механизма. Проведя вертикальные линии, до пересечения их с графиком, получаем соответствующие ординаты Y1,Y2,Y3,Y4,по которым можно судить о величине силы сопротивления, т.е.FC= YF. Результаты вычислений сведены в табл. 1.
Таблица 1.
Положения Параметры
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Yi(мм) |
0 |
24 |
100 |
49 |
0 |
0 |
0 |
0 |
Fi(H) |
0 |
1220,83 |
5086,8 |
2492,53 |
0 |
0 |
0 |
0 |
Планы скоростей.
Определим линейные скорости точек механизма и угловые скорости звеньев. Так как данный кривошипно-шатунный механизм плоский и совершает плоско-параллельное движение, то для определения скоростей будем использовать формулы плоско-параллельного движения твердого тела. При решении используем графо-аналитический метод. Выберем полюс плана скоростей P. Из него откладываем вектор скорости точки В.
Определим скорость точки В.

Введем
масштаб

Направление
скорости точкиС
определяется выражением
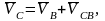 от конца вектора
от конца вектора
 перпендикулярно звену ВС откладываем
вектор
перпендикулярно звену ВС откладываем
вектор
 и проводим его до пересечения с осью х.
Имея точку пересечения, мы замыкаем
векторный треугольник вектором
и проводим его до пересечения с осью х.
Имея точку пересечения, мы замыкаем
векторный треугольник вектором
 .
Зная масштаб чертежа, получим:
.
Зная масштаб чертежа, получим:


Зная
величину и направления
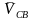 находим
находим
 .
Аналогичные
рассуждения проводим для оставшихся
семи положений.
.
Аналогичные
рассуждения проводим для оставшихся
семи положений.
Все получены значения скоростей сводим в табл. 2
Таблица 2.
Положения Параметры |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
VB(м/c) |
1,08 |
1,08 |
1,08 |
1,08 |
1,08 |
1,08 |
1,08 |
1,08 |
bc |
30 |
22 |
0 |
22 |
30 |
20 |
0 |
25 |
VCB(м/c) |
1,08 |
0,792 |
0 |
0,792 |
1,08 |
0,72 |
0 |
0,9 |
pc |
0 |
15 |
30 |
27 |
0 |
25 |
30 |
17 |
VC(м/c) |
0 |
0,54 |
1,08 |
0,972 |
0 |
0,9 |
1,08 |
0,612 |
ω2 |
7,2 |
5,28 |
0 |
5,28 |
7,2 |
4,8 |
0 |
6 |
Динамический анализ механизма
Построение плана ускорений.
План ускорений строится для одного положения механизма, в котором мощность достигает наибольшей величины. Для этого необходимо воспользоваться уже построенным планом скоростей.

 -
Сила сопротивления для заданного
положения.
-
Сила сопротивления для заданного
положения.
 -
Скорость точки, в которой приложена
сила.
-
Скорость точки, в которой приложена
сила.
Для заданного положения механизма построим план ускорений.
Определяем ускорение точки В. Звено 1 вращается равномерно, точка В этого звена обладает только нормальным ускорением, направленным вдоль звена 1 от точки Вк центру вращения звена А. На плане ускорений оно изображается отрезком πb.
Ускорение
точки В определяется выражением
 (
( ).
).
 .
Ускорение точки С находим по формуле:
.
Ускорение точки С находим по формуле:

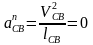
Выберем
масштаб плана ускорений. Пусть отрезок
соответствующий ускорению
 равен 50мм.
Тогда
равен 50мм.
Тогда
 .
.
От
конца вектора
 отложим вектор
отложим вектор
 .
Векторы
.
Векторы
 и
и
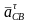 взаимно перпендикулярны. Замыкая
векторный треугольник вектором
взаимно перпендикулярны. Замыкая
векторный треугольник вектором
 мы находим его величину
мы находим его величину
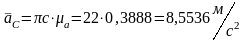

 – направлено
против
часовой стрелки.
– направлено
против
часовой стрелки.
Ускорение центров масс:
Кривошипа
–

Шатуна
–

Силовой анализ механизма.
Задачами силового анализа являются: определение сил инерции и моментов сил инерции звеньев, реакций в кинематических парах, уравновешивающей силы, момента движущих сил, мощности на валу кривошипа.
Определение инерционных нагрузок.
По
условию заданий кривошип вращается с
постоянной угловой скоростью, поэтому
его момент сил инерции
 .
.
Сила инерции кривошипа:
 ,
где
,
где

Отсюда:
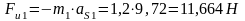
Сила инерции шатуна:
 ,
где
,
где

Отсюда:

Момент
силы инерции:
 ,
где
,
где


Сила инерции ползуна:
 ,
где
,
где

Отсюда:

Определение реакций в кинематических парах.
Для определения реакций в кинематических парах воспользуемся принципами Даламбера и статической определимости группы Ассура.
Вычертим группу Ассура в уже вычисленном масштабе, в 3-м положении. Отброшенные звенья заменяем реакциями. В соответствующих точках прикладываем силы веса звеньев Gi, силы инерции Fиi, силу полезного сопротивления FС .
Момент
силы инерции
 приводим к парам сил
приводим к парам сил
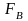 ,
приложенных в точкахВи
С,
и направленных перпендикулярно шатуну
ВС
величина этих сил
,
приложенных в точкахВи
С,
и направленных перпендикулярно шатуну
ВС
величина этих сил
 .
.
Силы направляем таким образом, что бы направление моментов пары сил совпало с направлением момента инерции, который направлен противоположно угловому ускорению.
Определим силы веса, для всего механизма.


Составляем уравнения равновесия:




Величины отрезков h1, h2, h3, h4,CB определяются замером на схеме.
Составим уравнения векторной суммы всех сил действующих на группу Ассура.
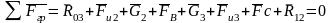
Выберем масштаб по максимальной силе. Пусть отрезок соответствующий
 =100
мм
тогда масштаб плана сил группы Ассура
=100
мм
тогда масштаб плана сил группы Ассура .
Результаты вычислений занесены в табл.
3
.
Результаты вычислений занесены в табл.
3
Таблица 3
|
|
|
|
|
|
|
Fc |
H |
5,25 |
31,49 |
29,4 |
8,55 |
9,8 |
2233,5 |
5086,8 |
мм |
0,044 |
0,619 |
0,58 |
0,168 |
0,193 |
44 |
100 |
Отрезками меньше 3мм пренебрегаем. Строим сумму векторов. Из плана сил:

Расчет ведущего звена.
Вычертим ведущее звено в масштабе. И прикладываем все действующие на него силы. Составим уравнение равновесия звена.


здесь R21=-R12, h5, h6, AB – отрезки измеренные непосредственно на схеме звена
Построение графика приведенных моментов сил сопротивлений.
Используя
рычаг Жуковского определим
 для всех положений механизма на рабочем
ходу, для этого к построенным планам
скоростей в точке С прикладываем
повернутую на 90 градусов силу сопротивления
P
, a
в точке b
перпендикулярно ab
уравновешивающую силу
.
для всех положений механизма на рабочем
ходу, для этого к построенным планам
скоростей в точке С прикладываем
повернутую на 90 градусов силу сопротивления
P
, a
в точке b
перпендикулярно ab
уравновешивающую силу
.
Уравнение
равновесия рычага Жуковского:

 ;
;

Где pc и pb – отрезки измеряемые на планах скоростей. Отрезок pb=30 мм постоянная величина для всех положений механизма.
Результаты вычислений сведены в табл. 4.
Таблица 4
Полож. |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
pc |
0 |
15 |
30 |
27 |
0 |
25 |
30 |
17 |
Fc |
0 |
1220,83 |
5086,8 |
2492,53 |
0 |
0 |
0 |
0 |
|
0 |
610,415 |
5086,8 |
2243,277 |
0 |
0 |
0 |
0 |
|
0 |
36,62 |
305,208 |
134,6 |
0 |
0 |
0 |
0 |
|
0 |
12 |
100 |
44 |
0 |
0 |
0 |
0 |

Строим
прямоугольную систему координат. По
оси абсцисс от начала координат отложим
отрезок l=80мм.
Отрезок l
делим на 8 равных частей, и из точек
деления восстанавливаем ординаты, на
которых откладываем отрезки
.
Полученные точки соединяем ломаной
линией, которая и будет графиком
 .
Масштаб поворота кривошипа:
.
Масштаб поворота кривошипа:

Определение мощности на валу кривошипа.
Интегрируя
графически диаграмму
получим диаграмму работ сил полезного
сопротивления
 .
.
Выберем полюсное расстояние H1 = 30мм, тогда масштаб диаграммы :

Так
как во время установившегося движения
работа движущих сил равна работе сил
полезного сопротивления, то соединив
прямой линией начало координат и точку
8’’ получим график работ движущих сил
 .
.
Продифференцировав этот график, получим величину приведенного момента движущих сил: