4) Строение атома

 

При химических реакциях ядра атомов остаются без изменений, изменяется лишь строение электронных оболочек вследствие перераспределения электронов между атомами. Способностью атомов отдавать или присоединять электроны определяются его химические свойства.

 

Электрон имеет двойственную (корпускулярно-волновую) природу. Благодаря волновым свойствам электроны в атоме могут иметь только строго определенные значения энергии, которые зависят от расстояния до ядра. Электроны, обладающие близкими значениями энергии образуют энергетический уровень. Он содержит строго определенное число электронов - максимально 2n². Энергетические уровни подразделяются на s-, p-, d- и f- подуровни; их число равно номеру уровня.

 

Квантовые числа электронов

 

Состояние каждого электрона в атоме обычно описывают с помощью четырех квантовых чисел: главного (n), орбитального (l), магнитного (m) и спинового (s). Первые три характеризуют движение электрона в пространстве, а четвертое - вокруг собственной оси.

 

Главное квантовое число (n). Определяет энергетический уровень электрона, удаленность уровня от ядра, размер электронного облака. Принимает целые значения (n = 1, 2, 3 ...) и соответствует номеру периода. Из периодической системы для любого элемента по номеру периода можно определить число энергетических уровней атома и какой энергетический уровень является внешним.

 

Пример.

Элемент кадмий Cd расположен в пятом периоде, значит n = 5. В его атоме электроны раcпределены по пяти энергетическим уровням (n = 1, n = 2, n = 3, n = 4, n = 5); внешним будет пятый уровень (n = 5).

 

Орбитальное квантовое число (l) характеризует геометрическую форму орбитали. Принимает значение целых чисел от 0 до (n - 1). Независимо от номера энергетического уровня, каждому значению орбитального квантового числа соответствует орбиталь особой формы. Набор орбиталей с одинаковыми значениями n называется энергетическим уровнем, c одинаковыми n и l - подуровнем.

 

Для

l=0 s- подуровень, s- орбиталь – орбиталь сфера

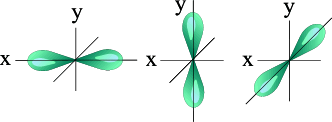
l=1 p- подуровень, p- орбиталь – орбиталь гантель

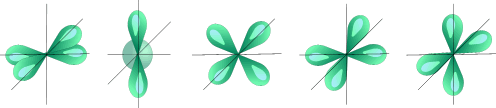
l=2 d- подуровень, d- орбиталь – орбиталь сложной формы

f-подуровень, f-орбиталь – орбиталь еще более сложной формы

 

S - орбиталь	Три p – орбитали

 

Пять d – орбиталей

 

На первом энергетическом уровне (n = 1) орбитальное квантовое число l принимает единственное значение l = (n - 1) = 0. Форма обитали - сферическая; на первом энергетическом только один подуровень - 1s. Для второго энергетического уровня (n = 2) орбитальное квантовое число может принимать два значения: l = 0, s- орбиталь - сфера большего размера, чем на первом энергетическом уровне; l =  1, p- орбиталь - гантель. Таким образом, на втором энергетическом уровне имеются два подуровня - 2s и 2p. Для третьего энергетического уровня (n = 3) орбитальное квантовое число l принимает три значения: l = 0, s- орбиталь - сфера большего размера, чем на втором энергетическом уровне; l = 1, p- орбиталь - гантель большего размера, чем на втором энергетическом уровне; l = 2, d- орбиталь сложной формы.

Таким образом, на третьем энергетическом уровне могут быть три энергетических подуровня - 3s, 3p и 3d.

 

Магнитное квантовое число (m) характеризует положение электронной орбитали в пространстве и принимает целочисленные значения от -I до +I, включая 0. Это означает, что для каждой формы орбитали существует (2l + 1) энергетически равноценных ориентации в пространстве.

Для s- орбитали (l = 0) такое положение одно и соответствует m = 0. Сфера не может иметь разные ориентации в пространстве.

Для p- орбитали (l = 1) - три равноценные ориентации в пространстве (2l + 1 = 3): m = -1, 0, +1.

Для d- орбитали (l = 2) - пять равноценных ориентаций в пространстве (2l + 1 = 5): m = -2, -1, 0, +1, +2.

Таким образом, на s- подуровне - одна, на p- подуровне - три, на d- подуровне - пять, на f- подуровне - 7 орбиталей.

 

Спиновое квантовое число (s) характеризует магнитный момент, возникающий при вращении электрона вокруг своей оси. Принимает только два значения +1/2 и –1/2 соответствующие противоположным направлениям вращения.

 

Принципы заполнения орбиталей

 

1.                  Принцип Паули. В атоме не может быть двух электронов, у которых значения всех квантовых чисел (n, l, m, s) были бы одинаковы, т.е. на каждой орбитали может находиться не более двух электронов (c противоположными спинами).

 

2.                  Правило Клечковского (принцип наименьшей энергии). В основном состоянии каждый электрон располагается так, чтобы его энергия была минимальной. Чем меньше сумма (n + l), тем меньше энергия орбитали. При заданном значении (n + l) наименьшую энергию имеет орбиталь с меньшим n. Энергия орбиталей возрастает в ряду:

 

1S < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 5d  4f < 6p < 7s.

 

3.                  Правило Хунда. Атом в основном состоянии должен иметь максимально возможное число неспаренных электронов в пределах определенного подуровня.

 

Полная электронная формула элемента

 

Запись, отражающая распределение электронов в атоме химического элемента по энергетическим уровням и подуровням, называется электронной конфигурацией этого атома. В основном (невозбужденном) состоянии атома все электроны удовлетворяют принципу минимальной энергии. Это значит, что сначала заполняются подуровни, для которых:

 

1)     Главное квантовое число n минимально;

 

2)     Внутри уровня сначала заполняется s- подуровень, затем p- и лишь затем d- (l минимально);

 

3)     Заполнение происходит так, чтобы (n + l) было минимально (правило Клечковского);

 

4)     В пределах одного подуровня электроны располагаются таким образом, чтобы их суммарный спин был максимален, т.е. содержал наибольшее число неспаренных электронов (правило Хунда).

 

5)     При заполнении электронных атомных орбиталей выполняется принцип Паули. Его следствием является, что энергетическому уровню с номером n может принадлежать не более чем 2n² электронов, расположенных на n²подуровнях.

 

Полная электронная формула элемента

 

Пример.

Цезий (Сs) находится в 6 периоде, его 55 электронов (порядковый номер 55) распределены по 6 энергетическим уровням и их подуровням. Cоблюдая последовательность заполнения электронами орбиталей получим:

 

₅₅Cs 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 4p⁶ 4d¹⁰ 5s² 5p⁶ 5d¹⁰ 6s¹

Основы атомной физики. Развитие представлений о строении атома. Модели Томсона и Резерфорда. Закономерности в атомных спектрах. Постулаты Бора. Опыты Франка и Герца. Квантование орбит. Боровская теория атома водорода. Неустойчивость атома в классических и полуклассических моделях.

1. Историческое развитие атомной модели вещества.

   1. Представление об атомной модели строении вещества возникло в античные времена (поэма Лукреция Кара, в которой изложена идея Демокрита о строении вещества).

   2. В 1647 году Пьер Гассенди возродил идею Демокрита об атомарном строении веществ.

      1. Он предположил, что все атомы различаются формой, величиной и весом.

      2. Атомы могут объединяться в группы, которые Гассенди назвал молекулами (от латинского слова "молес" – масса).

   3. Реальность существования атомов была доказана работами Бойля, Лавуазье, Ломоносова, Дальтона к началу XVIII века.

      1. Бойль и Лавуазье составили первые списки атомов, в которые наряду с химическими элементами включили и несуществующие субстанции (огонь у Бойля, теплотвор у Лавуазье).

      2. Ломоносов ввел понятия простых и смешанных тел в зависимости от сочетания атомов, их составляющих. Дальтон показал, что существуют химические закономерности, которые можно естественно объяснить, лишь используя представления об атомах.

   4. Первая модель атома была предложена Томсоном

1. Непрерывно заряженный положительным зарядом шар размером ~ 10^-10.

2. Внутри шара около положений равновесия колеблются электроны с суммарным отрицательным зарядом равным положительному заряду атома.

5. Следующая модель атома была предложена Резерфордом на основе наблюдений за рассеянием α-частиц.

   1. Атом имеет положительно заряженное ядро размером 10^-15  10^-14 м и массу, практически равную массе атома.

   2. Вокруг ядра по замкнутым орбитам движутся электроны.

   3. Равновесие поддерживается балансом кулоновской силы притяжения электронов к ядру и центробежной силы кругового движения (уравнение Резерфорда)

1. Недостатки модели Резерфорда:

• По модели Резерфорда спектр атома должен быть непрерывным.

• Ускоренное движение электронов должно сопровождаться испусканием электромагнитного излучения, а это приводит к непрерывной потере энергии электрона.

2. Исследованиями установлено, что излучение атомов имеет линейчатый спектр, который подчиняется уравнению Бальмера-Ридберга

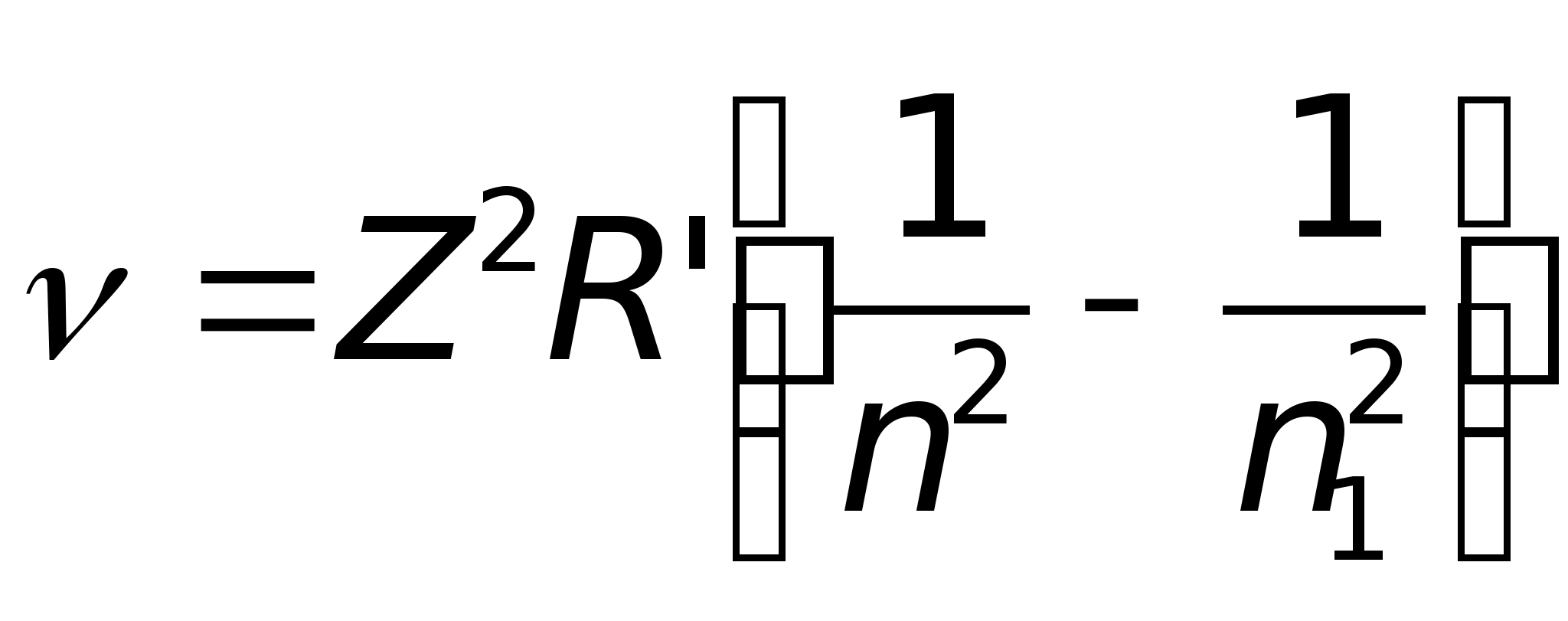
где   – постоянная Ридберга, Z – порядковый номер элемента, а n и n₁ – главные квантовые числа, причем n₁=n+1, n+2 и т.д.

1. Группа линий с одинаковым n называется серией:

• при n=1 – серия Лаймана;

• при n=2 – серия Бальмера;

• при n=3 – серия Пашена;

• при n=4 – серия Брэкета;

• при n=5 – серия Пфунда;

• при n=6 – серия Хэмфри.

2. Каждому значению квантового числа n в уравнении Бальмера-Ридберга соответствуетграница серии с наибольшей длиной частотой (при n₁=), называемой термом

3. Бор предложил модель, которая очень хорошо объясняла линейчатые спектры атомов. Модель бора опирается на постулаты Бора:

   1. В атоме существует набор стационарных состояний, находясь в которых атом не излучает электромагнитные волны (первый постулат – постулат стационарных состояний).

      1. Стационарному состоянию соответствует стационарная орбита, по которой электрон движется с ускорением, но при этом света не излучает.

      2. В стационарном состоянии атома электрон, движущийся по круговой орбите, имеет квантованные значения момента импульса, удовлетворяющие условию

(правило квантования)

где r_k – радиус k-ой орбиты, а k – целое число, равное количеству волн де Бройля для электрона, укладывающихся на длине круговой орбиты

2. При переходе атома из одного стационарного состояния в другое стационарное состояние испускается или поглощается один фотон (второй постулат – правило частот).

   1. Испускание фотона происходит при переходе атома из состояния с большей энергией в состояние с меньшей энергией.

   2. При обратном переходе происходит поглощение фотона.

   3. Энергия фотона равна модулю разности энергий в двух состояниях атома

при W_n>W_m – происходит излучение фотона;

при W_n<W_m – происходит поглощение фотона.

2. Набор возможных частот при переходах атома из одного состояния в другое определяет линейчатый спектр.

   1. Если домножить уравнение Бальмера-Ридберга на постоянную Планка, получим

2. Энергия атома в состоянии с главным квантовым числом n равна

• Энергия атома в основном состоянии (при n=1)

• Энергетические состояния с n>1 называются возбужденными состояниями.

• Важнейшей характеристикой возбужденных состояний является ограниченное время существования – =10-8. Атомы в основном состоянии могут иметь неограниченное время существования

2. Энергия связи электрона в атоме равна абсолютному значению энергетического состояния атома.

   1. В возбужденном состоянии (n>1) энергия связи электрона в атоме меньше, чем в основном состоянии.

   2. При n= энергия связи электрона в атоме равна нулю, то есть электрон может покинуть атом (ионизация). Энергия ионизации равна энергии связи электрона в атоме в основном состоянии.

   3. По величине энергии связи электрона в атоме в основном состоянии можно определить потенциал ионизации атома

3. Опыты Франка и Герца (домашнее задание).

5. Движение электрона в потенциальном поле ядра атома описывается стационарным уравнением Шредингера

где   – потенциальная (кулоновская) энергия электрона в поле ядра; W – энергия электрона в атоме, соответствующая волновой функции  при следующих условиях

• функция  должна быть конечной, непрерывной и однозначной;

• производные /х, /y и /z должны быть непрерывны;

• функция ² должна быть интегрируема (т.е. 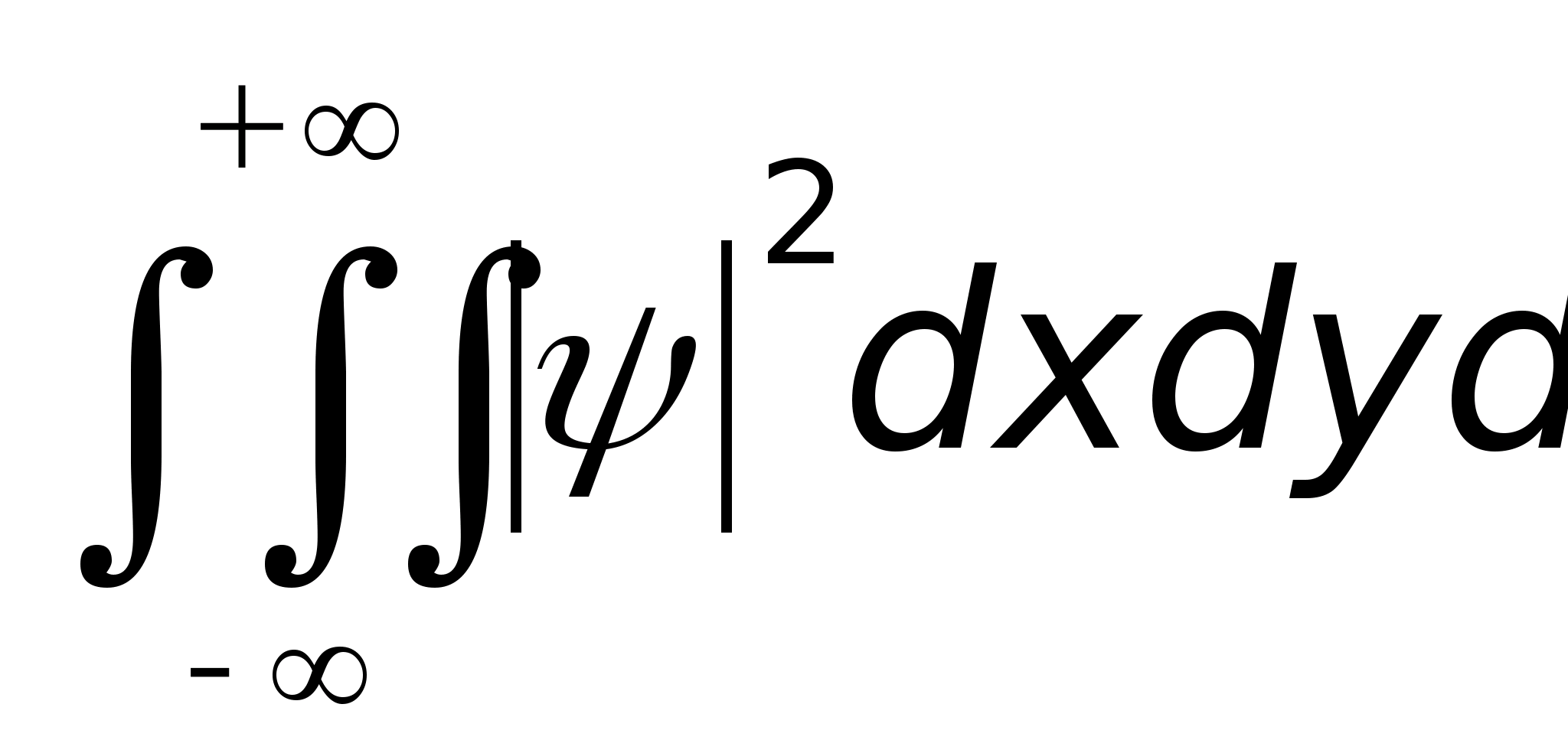  интеграл должен быть конечным).

1. При заданном виде U функции  называются собственными функциями, а соответствующие им значения W – собственными значениями энергии.

2. Совокупность собственных значений образует энергетический спектр электрона.

3. Решение стационарного уравнения Шредингера для электрона в центрально-симметричном кулоновском поле ядра приводит к тому, что значение момента импульса электрона в атоме квантуется по формуле

где l=0,1,…,(n-1) называется орбитальным квантовым числом.

1. В зависимости от значения орбитального квантового числа различают следующие состояния электрона в атоме;

• s-состояние при l=0;

• p-состояние при l=1;

• d-состояние при l=2;

• f-состояние при l=3;

и т. д.

5. Решая совместно уравнение Резерфорда и уравнения, определяющее правило квантования орбит, получим для водородоподобных атомов (атом с зарядом ядра Zq_e и одним электроном) выражение для радиуса стационарной круговой орбиты

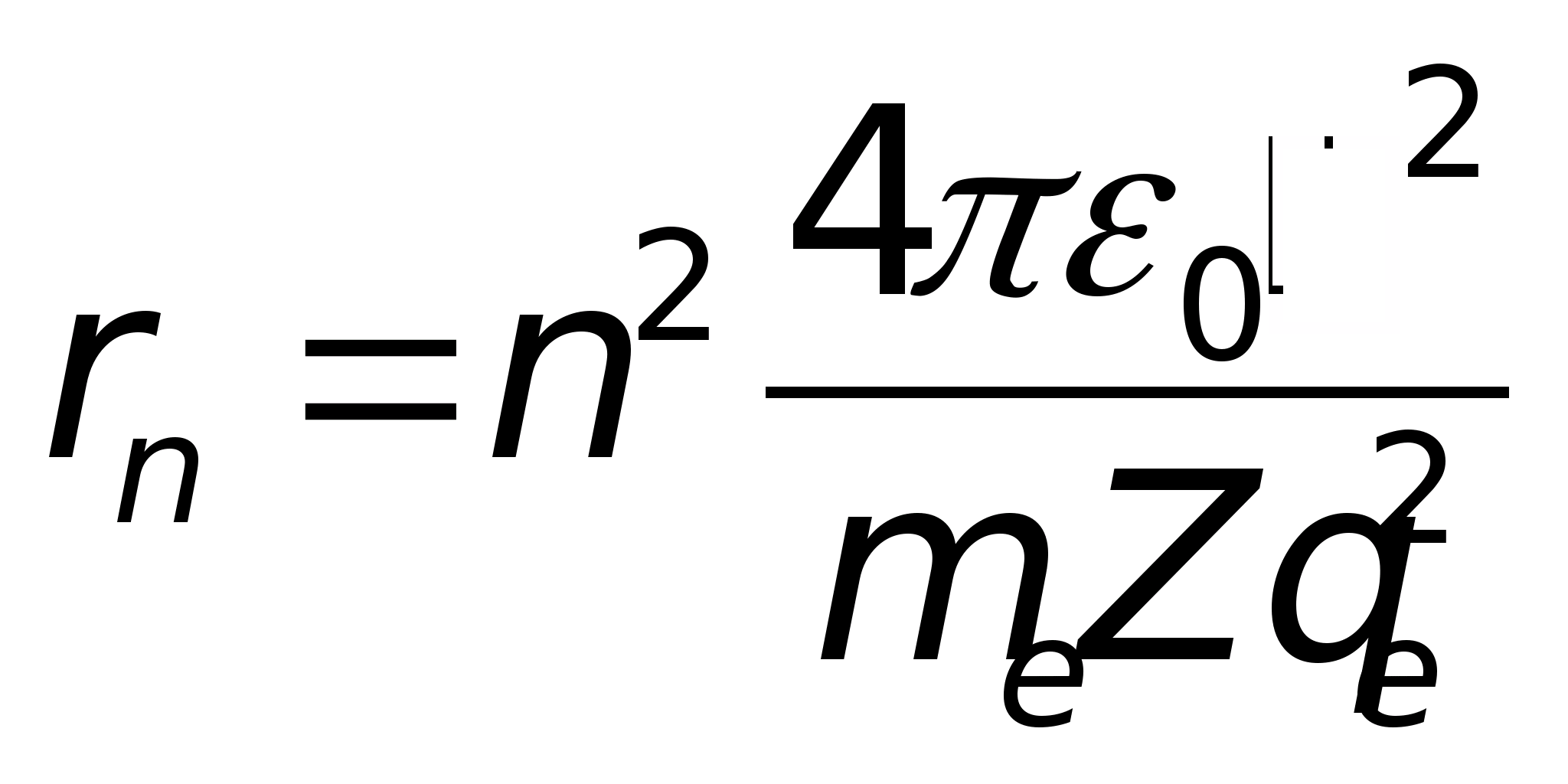
6. Состояние s электрона в атоме водорода при n=1 называется основным состоянием.

   1. Волновая функция электрона в основном состоянии атома водорода сферически симметрична, зависит только от расстояния r электрона от ядра и имеет вид

где С – постоянная, а а₀ – первый боровский радиус.

2. Величина первого боровского радиуса

хорошо совпадает со значением, полученным на основании кинетической теории газов.

3. Полная энергия электрона в водородоподобном атоме равна сумме потенциальной и кинетической энергий

а с учетом выражения для радиуса орбиты

4. При переходе атома водорода из состояния n в состояние m с меньшей энергией испускается квант света

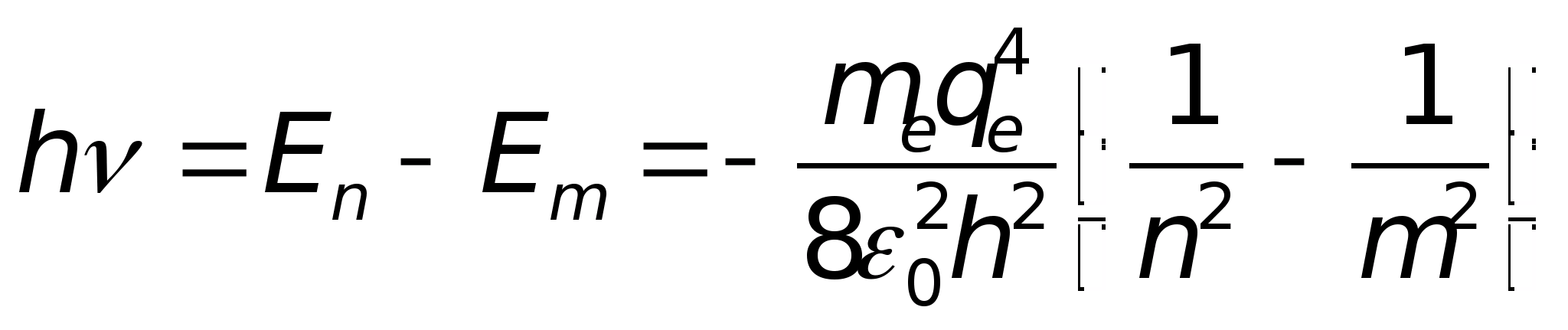
откуда значение постоянной Ридберга