2.10.1. Расчет относительных и абсолютных масс атомов и молекул

Относительные массы атомов и молекул определяются с использованием приведенных в таблице Д.И. Менделеева величин атомных масс. При этом, при проведении расчетов для учебных целей значения атомных масс элементов обычно округляются до целых чисел (за исключением хлора, атомная масса которого принимается равной 35,5).

Пример 1. Относительная атомная масса кальция А_r(Са)=40; относительная атомная масса платины А_r(Pt)=195.

Относительная масса молекулы рассчитывается как сумма относительных атомных масс составляющих данную молекулу атомов с учетом количества их вещества.

Пример 2. Относительная молярная масса серной кислоты:

М_r(H₂SO₄) = 2A_r(H) + A_r(S) + 4A_r(O) = 2·1 + 32 + 4·16 = 98.

Величины абсолютных масс атомов и молекул находятся делением массы 1 моль вещества на число Авогадро.

Пример 3. Определите массу одного атома кальция.

Решение. Атомная масса кальция составляет А_r(Са)=40 г/моль. Масса одного атома кальция окажется равной:

m(Ca)= А_r(Ca) : N_A =40 : 6,02·10²³ = 6,64·10^-23 г.

Пример 4. Определите массу одной молекулы серной кислоты.

Решение. Молярная масса серной кислоты равна М_r(H₂SO₄) = 98. Масса одной молекулы m(H₂SO₄) равна:

m(H₂SO₄) = М_r(H₂SO₄) : N_A = 98:6,02·10²³ = 16,28·10^-23 г.

2) Процессы, сопровождающиеся изменением степеней окисления реагирующих частиц, называют окислительно-восстановительными реакциями. В отличие от реакций ионного обмена окислительно-восстановительные реакции (ОВР) в водных растворах протекают, как правило, не мгновенно.

Эти реакции могут быть использованы для получения электрического тока. Равным образом процессы окисления и восстановления могут протекать под действием электрического тока. В этих двух случаях окислительно-восстановительные реакции относят к электрохимическим  процессам.

                В окислительно-восстановительной реакции

Zn + CuSO₄ = ZnSO₄ + Cu

атом  цинка   отдает два электрона

Zn -2e → Zn²⁺,

а ион меди принимает два  электрона

Cu²⁺ + 2e → Cu

Процесс потери электронов называют окислением, а вещество, отдающее электроны является восстановителем; цинк является восстановителем,  он окисляется. Процесс принятия электронов называют восстановлением, а вещество, принимающее электроны является окислителем; ион меди Cu²⁺является окислителем, он восстанавливается.

                Процессы окисления и восстановления протекают одновременно; окисление одного вещества всегда связано с восстановлением другого.

Критерий направления реакции в стандартных условиях.

Если в реакционной смеси присутствуют как исходные вещества, так и образуемые ими при протекании ОВР продукты реакции или, иначе говоря, два окислителя и два восстановителя, то направление реакции определяется тем, какой из окислителей в данных условиях в соответствии с уравнением Нернста окажется более сильным.

Любая запись уравнения ОВР предполагает определенный выбор окислителя в левой части уравнения. Если в стандартных условиях этот окислитель сильнее, реакция пойдет в прямом направлении, если нет – в обратном.

Стандартный потенциал окислительно-восстановительной пары, в которой окисленной формой является выбранный нами окислитель, назовем потенциалом окислителя φоОк, а стандартный потенциал другой пары, в которой восстановленной формой является выбранным нами восстановитель – потенциалом восстановителя φоВс.

Величину Δφо = φоОк – φоВс назовем стандартной разностью окислительно-восстановительных потенциалов.

Если Δφо > 0, реакция в стандартных условиях протекает в прямом направлении; если Δφо < 0, то в обратном.

Действительный смысл этого критерия: если Δφо> 0, то окислитель в левой части ионного уравнения ОВР сильнее второго окислителя в правой части уравнения.

                Эквивалентом окислителя (восстановителя) называется такое его наименьшее количество, которое соответствует одному присоединенному (отданному) им электрону в конкретном окислительно-восстановительном процессе.

Математически это утверждение будет соответствовать формуле:

          Эоx= νох/nē.

         Аналогично и для восстановителя:

Эred = νred/nē             

         При этом количество вещества эквивалента окислителя (νэох) и восстановителя (νэred) рассчитываются иначе, чем в случае химических эквивалентов.   

К окислительно-восстановительным системам также применим закон эквивалентов, согласно которому:

                            СN(ox).V(ox) = CN(red).V(red).

Для количественной характеристики окислительно-восстановительных процессов используют, в частности,  молярную массу эквивалентов окислителя и восстановителя определяемую по формуле - она равна частному от деления молярной массы окислителя или восстановителя на число электронов, принятых или отданных одной   структурной единицей вещества:

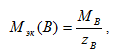                                                                (8.1)

где z_B – число эквивалентности, равное числу электронов, принятых или отданных одной   структурной единицей вещества.

Уравнения окислительно-восстановительных процессов составляются   с помощью метода   электронного баланса.

Процесс передачи электронов от окислителя к восстановителю является самопроизвольным и обратимым, при этом система в целом остается электрически нейтральной.

В окислительно-восстановительной системе, содержащей одновременно и окисленную и восстановленную фазы,  отсутствует градиент потенциала (разность зарядов), в ней всегда соблюдается электронный баланс.

Закон эквивалентов. Эквивалент. Эквивалентная масса и эквивалентный объем. Эквивалентные массы сложных соединений. Эквивалент. Эквивалентом вещества (элемента) Э называется такое его количество, которое взаимодействует с одним молем атомов водорода или вообще с одним эквивалентом любого другого вещества (элемента). Например, найдем эквивалент некоторых веществ: HCl – 1 моль, H2O. С одним молем водорода соединяется 1 моль хлора и ½ атомов кислорода, и следовательно эквиваленты равна соответственно 1 и ½. Эквивалентная масса и эквивалентный объем. Эквивалентная масса (Эм) называется масса одного эквивалента вещества (элемента). Эквивалентные массы ранее рассмотренных элементов равны Эм(Cl)=35.3 г/моль, Эм(O)=8 г/моль. Эквивалентную массу любого элемента можно определить по формуле: Эм=μ/СО, где СО- абсолютная величина степени окисления в соединениях. Поскольку большинство элементов имеют переменную степень окисления, то значения их эквивалентов в различных соединениях различно. Например найдем Если в задаче указаны объемы газов, то удобнее пользоваться понятием эквивалентный объем, вычисляемый с помощью закона Авогадро. Эквивалентным объемом называется объем занимаемый при н.у. одним эквивалентом вещества. Так 1 моль водорода, т.е. 2г. Занимает объем 22.4л., следовательно 1г. (т.е. одна эквивалентная масса), будет занимать 11,2л. Аналогично можно найти эквивалентный объем кислорода который равен 5.6л. Закон эквивалентов. Массы реагирующих веществ, а также продуктов реакции пропорциональны изх эквивалентным массам. m1/m2=Эм1/Эм2 Для химической реакции: νаА+νвВ=νсС+νдД справедливо nЭм(А)=nЭм(В)=nЭм(С)=nЭм(Д) Где nЭм – число эквивалентных масс. Поэтому если известно число эквивалентных масс одного из веществ, то отпадает необходимость в подсчете числа Эм оставшихся веществ. Очевидно, что число эквивалентных масс равно отношению массы вещества к эквивалентной массе. Закон эквивалентов для эквивалентных объемов записывается в следующем виде: V1/V2=Эv1/Эv2 Эквивалентные массы сложных соединений. На основе закона эквивалентных масс справедливы следующие формулы для расчета Эм: Эм(оксида)=μ(оксида)/∑СОэл-та ,где ∑СОэл-та – суммарная степень окисления одного из элементов (она равна произведению степери окисления элемента на число атомов этого элемента) Эм(соли)=μ(соли)/∑z , где ∑z – суммарный заряд иона (катиона или аниона). Эм(кислоты)=μ(кислоты)/nh(основность-число Н) Эм(основания)=μ(основания)/nон(кислотность основания – число ОН) H3PO4+2KOH=K2HPO4+2H2O 3Ca(OH)2+H3PO4=(CaOH)3PO4+3H2O Al2(SO4)3+6KOH=2Al(OH)3+3K2SO4

Эквивалентной массой называется масса 1 эквивалента вещества. Пример 1. Определить эквивалент и эквивалентную массу элементов в соединениях НВr, Н₂О и NН₃. Решение. В указанных соединениях с одним молем атомов водорода соединяется 1 моль атомов брома, 1/2 моля атомов кислорода и 1/3 моля атомов азота. Следовательно, согласно определению, эквиваленты брома, кислорода и азота равны соответственно 1 молю, 1/2 и 1/3 моля. Исходя из атомных масс этих элементов, находим, что эквивалентная масса брома равна 79,9 г/моль, кислорода - 16:2=8 г/моль, азота - 14:3 =4,67 г/моль. Для определения эквивалента (эквивалентной массы) элемента необязательно исходить из его соединения с водородом. Эквивалент (эквивалентную массу) можно вычислить по составу соединения данного элемента с любым другим, эквивалент которого известен. Пример 2. При соединении 5,6 г железа с серой образовалось 8,8 г сульфида железа. Найти эквивалентную массу железа и его эквивалент, если известно, что эквивалентная масса серы равна 16 г/моль. Решение. Из условия задачи следует, что в сульфиде железа на 5,6 г железа приходится 8,8-5,6=3,2 г серы. Согласно закону эквивалентов, массы взаимо-действующих веществ прямо пропорциональны их эквивалентным массам:   Следовательно, 5,6 г железа эквивалентны 3,2 г серы Э г/моль » 16 г/моль серы    Молярная масса атомов железа численно совпадает с его относительной атомной массой и составляет 56 г/моль. Поскольку эквивалентная масса железа (28 г/моль) в два раза меньше молярной массы его атомов, то в 1 моле железа содержится 2 эквивалента. Следовательно, эквивалент железа равен 1/2 моля. На основе законов эквивалентов можно вывести следующие формулы для вычисления эквивалентных масс сложных веществ – оксидов, кислот, оснований и солей: где М – молярная масса соединений, г/моль; Э – их эквивалентная масса. Пример 3. Вычислить эквиваленты Н₂SO₄ и Аl(ОН)₃ в реакциях, выражаемых уравнениями Н₂SO₄ + КОН = КНSO₄ + Н₂O; (1) Н₂SO₄ + Mg = MgSO₄ + Н₂; (2) Al(OH)₃ + HCl = Al(OH)₂Cl + H₂O; (3) Al(OH)₃ + 3HNO₃ = Al(NO₃)₃ + 3H₂O. (4) Решение. Эквивалент сложного вещества, как и эквивалент элемента, может иметь различные значения и зависит от того, в какую реакцию вступает это вещество.

3) Закон Авогадро. Открыт в 1811 г. итальянским физиком А.Авогадро. В равных объемах различных газов при одинаковых давлении и температуре содержится одинаковое число молекул.

 

При нормальных условиях (температура 0^оС=273,15К и давление 1 атм =760 мм рт.ст.= 101325 Па=101,325кПа) один моль любого газа содержит 6,022045^.10²³ =6,02^.10²³ молекул  (постоянная Авогадро) и занимает объем 22 414 см³⁼22,4 дм³ .

Закон Авогадро позволяет определить молярную массу газа  если известна его плотность (ρ)  при нормальных условиях

                                             М_В=22,4 ρ                                     (1.7)

или плотность при нормальных условиях, если известна молярная масса. Можно также определить молярную массу неизвестного газа (М_х), зная молярную массу известного газа (М_В) и отношение плотностей этих газов (ρ_х/ρ_В)

                                                                                  (1.8)

                Отношение ρ_х/ρ_В носит название относительной плотности  одного газа по другому и обозначается буквой D.  Например, если использовать относительную плотность неизвестного газа по водороду и воздуху, то формула(1.8) запишется следующим образом:

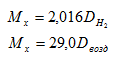                                                                                  (1.8а)(1.8б)

                                                                             

                Если условия, при которых находится газ, отличаются от нормальных, то для определения молярной массы газа можно использовать уравнение состояния идеальных газов Менделеева ^_ Клапейрона

                                                                                     (1.9)

где р  ^_  давление газа; V ^_  объем  газа; m_B ^_  масса газа; М_В ^_ молярная масса газа; Т – температура в градусах термодинамической шкалы Кельвина (К); R ^_универсальная газовая постоянная, равная  8,314 Дж/(моль^.К), или (л^.кПа)/(моль^.К) в СИ, или  0,08206 (л^.атм)/(моль^.К), если давление выражено в атмосферах, или 62,36 (л^.мм рт. ст.)/( моль^.К), если давление выражено в мм ртутного столба.

Моля́рный объём — объём одного моль вещества, величина, получающаяся от деления молярной массы наплотность. Характеризует плотность упаковки молекул.

Значение N_A = 6,022…×10²³ называется числом Авогадро в честь итальянского химика Амедео Авогадро. Это универсальная постоянная для мельчайших частиц любого вещества.

Именно такое количество молекул содержит 1 моль кислорода О₂, такое же количество атомов в 1 моль железа (Fe), молекул в 1 моль воды H₂O и т. д.

Согласно закону Авогадро, 1 моль идеального газа при нормальных условиях имеет один и тот же объёмV_m = 22,413 996(39) л/моль^[1]. При нормальных условиях большинство газов близки к идеальным, поэтому вся справочная информация о молярном объёме химических элементов относится к их конденсированным фазам, если не оговорено обратное.

Хорошо известный закон Бойля-Мариотта был установлен английским физиком Бойлем в 1662 г. и независимо от него французским ученым Мариоттом в 1679 г.

Рис. 2.1

Для данной массы газа m при неизменной температуре Т произведение давления на объем есть величина постоянная:

.

Процесс, происходящий при постоянной температуре, называется изотермическим. График этого процесса в координатах p– V представлен на рис. 2.1.

Закон, связывающий объем газа V и его температуру t, измеренную в градусах Цельсия, был установлен французским ученым Гей-Люссаком в 1802 г.

Для данной массы m при постоянном давлении р объем газа линейно зависит от температуры:

Рис. 2.2 ,

где V₀ – объем газа при нуле градусов Цельсия, α – коэффициент объемного расширения, t – температура по шкале Цельсия.

График этого процесса, называемого изобарическим, представлен на рис. 2.2. Коэффициент α для всех газов равен

.

Закон, связывающий давление газа р и его температуру t, установлен Шарлем.

Рис. 2.3

Для данной массы m при постоянном объеме V давление газа линейно зависит от температуры:

,

где p₀ – давление газа при нуле градусов Цельсия, β – коэффициент объемного расширения, t – температура по шкале Цельсия.

График этого процесса, называемого изохорическим, представлен на рис. 2.3. Коэффициент β для всех газов равен

,

В координатах Р–V изобарический и изохорический процессы представлены на рис. 2.4.

Рис. 2.4

Опытные законы Бойля-Мариотта, Гей-Люссака и Шарля справедливы для широкого интервала давлений, объемов и температур. Однако когда давления превышают атмосферное в 300-400 раз, или температуры очень высоки, наблюдаются отклонения от этих законов. Тем не менее, во многих случаях эти законы удобны для практического применения.

Если бы существовал газ, для которого не было бы отклонений от этих законов, то такой газ был бы идеальным газом.

Объединенный газовый закон

Объединенный газовый закон

Объединяя законы Бойля - Мариотта и Гей-Люссака (уравнения 1 и 2), можно получить следующее уравнение:

 (3)

которое является математическим выражением объединенного газового закона, или закона состояния газов. Он позволяет вычислить, например, объем газа при определенных температуре и давлении, если известен его объем при других значениях температуры и давления.

Объединенный газовый закон можно также записать в другой форме:

Точное значение постоянной в правой части этого уравнения зависит от количества газа. Если количество газа равно одному молю (см. гл. 4), то соответствующая постоянная обозначается буквой R и называется молярная газовая постоянная, или просто газовая постоянная. Если давление выражено в атмосферах, постоянная R имеет значение

R = 8,314 Дж*К* моль-1

Объединенный газовый закон для одного моля газа приобретает вид

где Vm- объем одного моля газа. Для п молей газа получается уравнение

 (4)

В такой форме объединенный газовый закон называется уравнением состояния идеального газа. Уравнение состояния это уравнение, связывающее между собой параметры состояния газа-давление, объем и температуру.

Газ, который полностью подчиняется уравнению состояния идеального газа, называется идеальный газ. Такой газ не существует в действительности. Реальные газы хорошо подчиняются уравнению состояния идеального газа при низких давлениях и высоких температурах. Отклонения в поведении реальных газов от предписываемш уравнением состояния идеального газа подробно обсуждаются ниже.

Вычисление относительной молекулярной массы с помощью уравнения состояние идеального газа. Уравнение состояния идеального газа позволяет проводить прямые вычисления относительной молекулярной массы газа M1. Введем понятие относительной молекулярной массы, основываясь на уже знакомом нам (из гл. 1) определении относительной атомной массы A1. Для газа, состоящего из простых молекул, относительная молекулярная масса представляет собой сумму относительных атомных масс всех атомов, входящих в молекулу. Например, для диоксида углерода

Относительная молекулярная масса, выраженная в граммах на моль, называется молярной массой (см. гл. 4). Следовательно, молярная масса CO2 равна 44 г/моль. Два моля CO2 имеют массу 88 г, а и молей-массу п -44 г. В общем случае можно записать

 

где n-количество вещества в молях (т.е. число молей данного вещества), т-масса вещества в граммах, a M-его молярная масса.

Подстановка полученного выражения для п в уравнение состояния идеального газа (4) дает

 (5)

Это уравнение позволяет, зная массу и объем газа при определенных температуре и давлении, вычислить его молярную массу М. А поскольку

M = M (г/моль), то полученный результат непосредственно дает относительную молекулярную массу М.

Уравнение Клапейрона-Менделеева. Связь между числом молей газа, его температурой, объемом и давлением.

Газы нередко бывают реагентами и продуктами в химических реакциях. Не всегда удается заставить их реагировать между собой при нормальных условиях. Поэтому нужно научиться определять число молей газов в условиях, отличных от нормальных.

Для этого используют уравнение состояния идеального газа (его также называют уравнением Клапейрона-Менделеева):

PV = nRT

где n – число молей газа;

P – давление газа (например, в атм;

V – объем газа (в литрах);

T – температура газа (в кельвинах);

R – газовая постоянная (0,0821 л·атм/моль·K).

Например, в колбе объемом 2,6 л находится кислород при давлении 2,3 атм и температуре 26 ^оС. Вопрос: сколько молей O₂ содержится в колбе?

Из газового закона найдем искомое число молей n:

Не следует забывать преобразовывать температуру из градусов Цельсия в кельвины: (273 ^оС + 26 ^оС) = 299 K. Вообще говоря, чтобы не ошибиться в подобных вычислениях, нужно внимательно следить за размерностью величин, подставляемых в уравнение Клапейрона-Менделеева. Если давление дается в мм ртутного столба, то нужно перевести его в атмосферы, исходя из соотношения: 1 атм = 760 мм рт. ст. Давление, заданное в паскалях (Па), также можно перевести в атмосферы, исходя из того, что 101325 Па = 1 атм.

** Можно проводить вычисления и в системе СИ, где объем измеряется в м³, а давление - в Па. Тогда используется значение газовой постоянной для системы СИ: R = 8,314 Дж/K·моль. В этом параграфе мы будем использовать объем в литрах и давление в атм.

Решим такую задачу: некоторое количество газа гелия при 78 ^оС и давлении 45,6 атм занимает объем 16,5 л. Каков объем этого газа при нормальных условиях? Сколько это молей гелия? Можно, конечно, просто подставить данные нам значения в уравнение Клапейрона-Менделеева и сразу вычислить число молей n. Но что делать, если на экзамене вы забыли точное значение газовой постоянной R?

Газовую постоянную не нужно запоминать – ее можно легко вычислить в любой момент. Действительно, 1 моль газа при нормальных условиях (1 атм и 273 К) занимает объем 22,4 л. Тогда:

Парциальное давление идеального газа в смеси равно давлению, которое будет оказываться, если бы он занимал тот же объём, что и вся смесь газов, при той же температуре. Причина этого в том, что между молекулами идеального газа не действуют силы притяжения или отталкивания, их соударения между собой и со стенками сосуда абсолютно упруги, а время взаимодействия между молекулами пренебрежимо мало по сравнению со средним временем между столкновениями. Реально существующие газы очень близко подходят к этому идеалу. Следствием этого является то, что общее давление смеси идеальных газов равно сумме парциальных давлений каждого газа в смеси, как это формулирует закон Дальтона^[3]. Например, дана смесь идеального газа из азота(N₂), водорода (H₂) и аммиака (NH₃):

, где:

 = общему давлению в газовой смеси

 = парциальному давлению азота (N₂)

 = парциальному давлению водорода (H₂)

 = парциальному давлению аммиака (NH₃)