16. Классификация объектов вероятностным подходом. Закон Бейеса.

Случайное событие – это такое, для которого невозможно предсказать его точный результат в каждом конкретном случае. Однако при большом числе реализаций эти события можно характеризовать средними результатами, стабильными и воспроизводимыми. В основе этих представлений лежит понятие вероятности.

Рассмотрим опыт с несколькими возможными исходами, каждый конкретный результат которого в точности не предсказуем. Множество всех исходов назовем 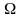– пространство элементарных событий. Событие А есть подмножество множества (лучше М), обладающее некоторыми свойствами, приводимыми ниже.

По определению вероятностью P(A) события А называют величину, удовлетворяющую трем аксиомам:

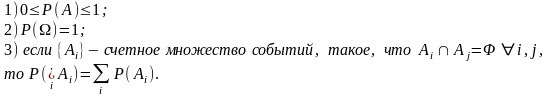
Здесь через 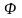обозначено пустое множество. К этому можно добавить, что

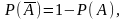где – событие, дополняющее А до .

Если могут произойти два события – А и В, то можно говорить о трех различных вероятностях:

событие А происходит с вероятностью P(A),

событие В происходит с вероятностью P(В),

события А и В происходят одновременно с вероятностью P(A, В), ее называют вероятностью совместного события, или совместной вероятностью.

Пусть 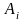(i=1, 2, … n) и В – случайные события. Условную вероятность того, что произойдет событие , при условии, что произошло событие В, записывают так: P(A_i/B). Это – апостериорная вероятность. Ее плотность обозначают p(A_i/B). B – известная (фактическая) величина, А – случайная величина.

Значение условной вероятности P(A_i/B) можно вычислить по теореме Бейеса: 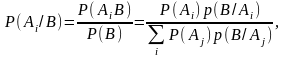поскольку

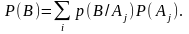
Действительно, 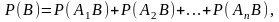а при этом

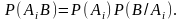Здесь 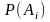- априорная вероятность события .

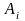Пример апостериорной плотности вероятности. Случай одномерного гауссового распределения:

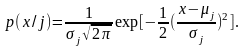
Эта плотность распределения является функцией двух параметров: – математическое ожидание и 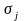– среднеквадратичное отклонение. Эти параметры могут быть вычислены по N опытам, в каждом из которых измеряются величина

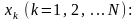
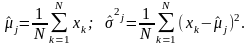
17. Решающее правило при вероятностном подходе.

С помощью понятия об апостериорных вероятностях можно подойти к разработке метода автоматической классификации.

Пусть 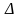(В конспекте М) – сепарабельное пространство признаков, а 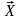– вектор, представляющий к-ый класс, сепарабельное пространство по определению может быть разделено на классы. Априорная вероятность того, что данная реализация относится к классу с номером к, есть

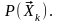
Проблема заключается в том, чтобы отнести неизвестный предъявляемый объект к одному из известных классов Ck с минимальной ошибкой. Для этого выполняют n измерений в соответствии с признаками, выбранными надлежащим образом. В результате получают вектор измерений 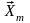, для которого можно найти условную вероятность или ее плотность:

Решение об отнесении неизвестного объекта к классу с номером к можно считать оправданным, если для любого j выполняется условие:

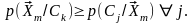Эти вероятности могут быть вычислены согласно теореме Бейеса по тем условным вероятностям , которые получаются непосредственно в процессе измерений:

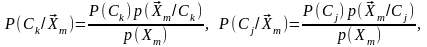
Откуда следует решающее правило:

Процесс разделения на классы, как правило, связан с некоторым риском. Правильной или неверной классификации можно придать определенную «цену». Введем решающее правило d, в соответствии с которым каждый предъявляемый объект по результатам измерений вызывает действие d_i. Оно определяется отнесением к классу .

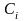Риск принятия решений.

Пусть 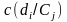– условная цена принятия решения 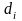, если известно, что объект принадлежит классу 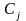. Среднее значение цены, связанной с принятием решения в случае, когда предъявлен объект , определяет средний риск принятия данного решения: 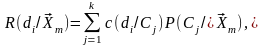где правая часть равенства получена по формуле Бейеса.

Средняя цена для решающего правила d, если известно, что предъявлен объект , есть

Пусть 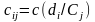– цена, связанная с решением отнести к классу , если известно, что искомый класс есть . Функцию цены в этом случае представим в следующем виде:

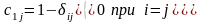
Для заданного средняя цена отнесения его к классу будет:

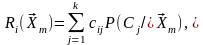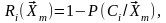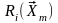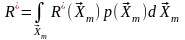тогда и решающее правило преобразуется к виду поскольку стремятся минимизировать цену . При этом вероятность ошибочного решения или