11. Алгоритм класс-ции на базе контролируемого обучения (к-средних)

Цель алгоритма – оптимальным образом разделить заданные объекты на классы. Оптимальность связанна с наиболее удаленным выбором центров классов и компактным распределением оставшихся объектов по классам вокруг этих центров.

Исходные данные: N Объектов, K классов.

1 шаг:

Формируем К ядер. Затем вокруг них формируем области объектов по принципу минимальных расстояний.(Евклидово расстояние)

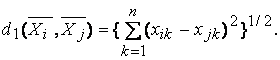
, где n = 2 (координатная плоскость)

На i-том шаге х связывается с определенным ядром, если расстояние от вектора х до этого ядра меньше, чем до остальных К – 1 ядер.

2 шаг:

Определяются новые элементы, претендующие стать ядрами классов. Ими становятся векторы х, обеспечивающие минимальные средневекторные (или среднеквадратичные) отклонения

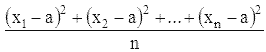
по своему классу. (Искать можно так: суммируем все Х координаты объектов данного класса и делим на количество объектов в класса. Тоже самое делаем с координатой У. Полученные х и у будут являться центром масс.) Если хотя бы в одном из классов поменялось ядро, то переходим к 1 шагу, иначе алгоритм закончен.

12. Алгоритм классификации на базе самообучения (Максимин)

Цель: разделить заданное множество объектов на классы, исходя из произвольного выбора.

Алгоритм является алгоритмом самообучения.

Исходные данные: N объектов.

1 шаг:

Случайно назначаем центр n1, максимально удаленный от него объект становится ядром второго класса n2.

2 шаг:

Связываем остальные объекты с этими центрами по принципу минимального расстояния.(Евклидово расстояние)

3 шаг:

В каждом классе находим максимально удаленные объекты от ядра. Среди них выбирается максимально отдаленный от своего ядра, он и становится претендентом на ядро очередного класса. Если расстояние от него до ядра больше, чем 1 / 2 среднего расстояния между существующими ядрами (например, есть три класса, если

dn4 > (d12 + d13 + d23) / (2*classesCount(В нашем случае 3))

) , то объект-претендент становится ядром и переходим ко второму шагу, иначе алгоритм закончен.

13. Расстояние между классами (частный случай)

/* Введем понятие расстояние между классами, исходя из гипотезы о том, что оно должно было бы обладать двумя основными свойствами.

1. Компактность, выражающееся в том, что точки, представляющие объекты одного класса, расположены друг к другу ближе, чем к точкам, относящимся к другим классам.

2. Сепарабельность, отражающее тот факт, что классы ограничены и не пересекаются между собой.

На практике оба эти свойства выполняются не всегда, так как зависят от того, насколько удачно выбраны признаки. Понятие расстояния позволяет оценить степень сходства как между отдельными реализациями, так и между целыми классами. С точки зрения распознавания образов можно полагать, что чем меньше расстояние, тем сходство должно быть больше. Например, оценить сходство величиной к, обратной расстоянию d: k=1/d.

Нередко признаки объектов, между которыми нужно установить сходство, не могут быть выражены в числах. Наличие или отсутствие признака можно кодировать двоичным кодом. Пусть некоторый образ X_i представляется в виде вектора: 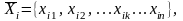где первый индекс – это номер реализации, а второй индекс – номер признака. Образ можно записать в виде последовательности двоичных символов в соответствии с правилом: если i-ый объект обладает к-ым признаком, то Xik=1, иначе Xik=0. */

Пример: Исходные данные для классификации представлены в следующей таблице

Э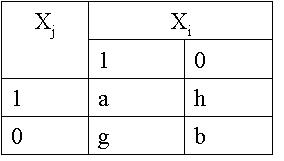 ту таблицу можно представить как класс С, а множество векторов как Х= 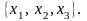В данном случае класс фруктов состоит из объединения непересекающихся подмножеств, каждое из которых включает в себя единственный объект. Поэтому такая классификация является тривиальной. Можно провести более тонкую классификацию, если для каждой пары предъявлений последовательно установить степень их сходства и различия. Тогда таблицу соответствия двух реализаций Xi и Xj можно представить следующим образом:

а – число случаев, когда Xi и Xj обладают одним и тем же признаком.

b – число случаев, когда Xi и Xj не обладают никакими общими признаками.

h – число случаев, когда Xi не обладает признаками, присущими Xj.

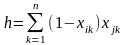
g – число случаев, когда Xi обладает признаком, отсутствующим у Xj.

Отсюда следует, что чем больше сходств между Xi и Xj, тем больше должен быть коэффициент а и тем сильнее он должен отличаться от других коэффициентов. Можно ввести функцию сходства, характеризующуюся следующими свойствами:

1. Она должна быть возрастающей в зависимости от а.

2. Она должна быть убывающей в зависимости от b.

3. Она должна быть симметричной относительно g и h.

Эту функцию, для которой известно несколько различных вариантов вычисления, называют двоичным расстоянием: (несколько их)

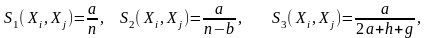
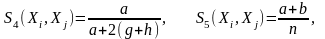
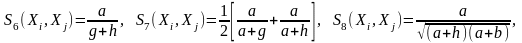n – число признаков.

Найдем сходства между объектами х1 х2 и х3.

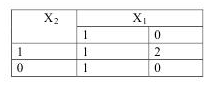
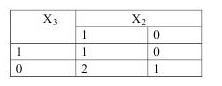
Х2 и Х3 Х3 и Х2

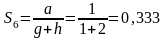
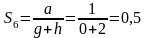
В соответствии с выбранными критериями отбора получаем, что объекты X2 и X3 больше схоже, чем объекты X1 и X2, т.е. яблоко и банан более схоже чем вишня и яблоко.