- •Распознавание образов. Общие положения.
- •Объекты в распознавании образов
- •Классификация объектов. Понятие расстояния между объектами.
- •Две группы методов распознавания и их особенности.
- •Разделяющая функция. Решающее правило. Пример разделения на два класса.
- •Линейные разделяющие функции для n классов. 1-ый случай разделения
- •Линейные разделяющие функции для n классов. 2-ой случай разделения
- •Обучение в решении задачи классификации
- •Обучение с учителем и без учителя
- •11. Алгоритм класс-ции на базе контролируемого обучения (к-средних)
- •12. Алгоритм классификации на базе самообучения (Максимин)
- •13. Расстояние между классами (частный случай)
- •14. Расстояние между списками
- •15. Метод динамического программирования
- •16. Классификация объектов вероятностным подходом. Закон Бейеса.
- •17. Решающее правило при вероятностном подходе.
- •18. Разделение объектов на два класса при вероятностном подходе
- •19. Устройство автоматической классификации «Персептрон»
- •20. Критерий коррекции весовых коэф-в для классификации объектов
- •21. Алгоритм классификации объектов на n классов (Персептрон)
- •22. Метод потенциалов
- •23. Иерархическое группирование
- •24. Определение иерархии
- •25. Пример метода иерархической классификации
- •26. Постановка задачи синтаксического распознавания образов. Структурная схема системы распознавания. (V)
- •27. Понятия языка, строки, грамматики. Описание грамматики и ее компонентов.
- •28. Связь между автоматами и грамматиками при синтаксическом распознавании. (V)
- •29. Постановка задачи синтаксического распознавания образов. Грамматический разбор сверху вниз (привести пример) (V)
- •30. Постановка задачи синтаксического распознавания образов. Грамматический разбор снизу вверх (привести пример). (V)
- •31. Применение методов синтаксического распознавания для двумерных объектов. Использование языка описания изображений pdl (привести пример). (V)
- •32. Стохастические грамматики и языки (привести пример).
- •33. Алгоритм вывода цепочечных грамматик. (V)
- •3 Части построения Алгоритма:
- •34. Алгоритм вывода двумерных грамматик.(V)
- •35. Общие понятия систем распознавания
- •36. Проблематика задач создания систем распознавания
- •37. Формулировка задач создания систем распознавания и методы их решения. Задачи 1,2
- •38. Формулировка задач создания ср и их решение. Задачи 3,4
- •39. Формулировка задач создания ср и их решение. Задачи 5,6
- •40. Принципы классификации ср (1, 2)
- •Однородность информации для описания распознаваемых объектов и явлений
- •Способ получения апостериорной информации
- •41. Принципы классификации ср (3, 4)
- •Количество первоначальной априорной информации
- •Характер информации признаках распознавания
- •42. Обучающиеся и самообучающиеся ср (структурные схемы)
- •43. Биологические основы функционирования нейрона
- •44. Принципы построения и действия искусственной нейронной сети
- •45. Инс в виде многослойного персептрона
- •46. Решение задач с помощью нс на базе многослойного персептрона
Линейные разделяющие функции для n классов. 2-ой случай разделения
Каждый класс отделяется от любого другого класса «индивидуальной» разделяющей поверхностью, т.е. классы попарно разделимы. В этом случае существует М(М-1)/2 (число сочетаний из М классов по два) разделяющих поверхностей. Решающие функции имеют вид
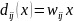 и
обладают тем свойством, что если образ
х принадлежит классу
и
обладают тем свойством, что если образ
х принадлежит классу
 то
то
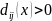 для всех
для всех
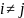 ;
кроме того,
;
кроме того,
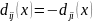
О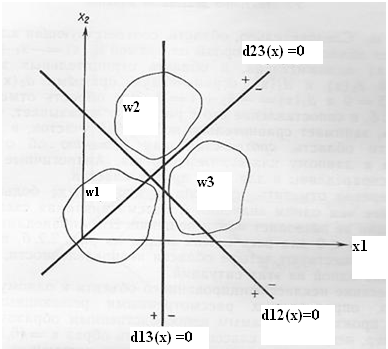 чевидно,
что ни
один класс нельзя отделить от всех
остальных с помощью единственной
разделяющей поверхности.
Каждая из приведенных на рис. границ
обеспечивает разделение 2-ух классов.
Так, например, хотя граница
чевидно,
что ни
один класс нельзя отделить от всех
остальных с помощью единственной
разделяющей поверхности.
Каждая из приведенных на рис. границ
обеспечивает разделение 2-ух классов.
Так, например, хотя граница
 проходит
через класс w3
, она дает эффективное разделение только
для классов w1
и w2.
проходит
через класс w3
, она дает эффективное разделение только
для классов w1
и w2.
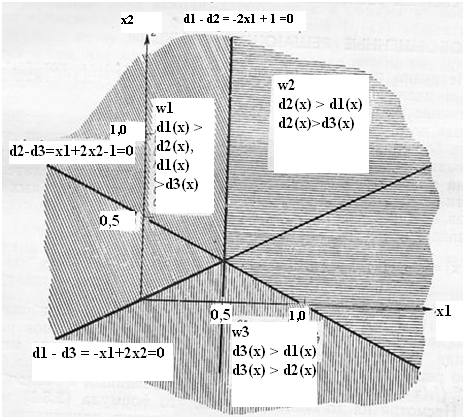
Пусть
решающие функции имеют следующий вид:
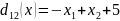 ;
;
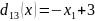 ;
;
 ;
;
Разделяющие
границы получим, приравнивая решающие
функции нулю. Здесь области решений
могут содержать несколько зон, где
соответствующие функции положительны.
Область, относящаяся к классу w1,
определяется значениями образа х, при
которых
 и
и Значение решающей функции
Значение решающей функции
 в этой области не существенно, поскольку
данная решающая функция никак не связана
с классом w1.
в этой области не существенно, поскольку
данная решающая функция никак не связана
с классом w1.
Области,
определяемые тремя указанными решающими
функциями, представлены на рис ниже.
Для выделения областей, соответствующих
разным классам, использовано условие
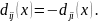 Поэтому поскольку
,
Поэтому поскольку
,
 ;
то зона положительности функции
;
то зона положительности функции
 совпадает с зоной отрицательности
функции
совпадает с зоной отрицательности
функции
 области решения безграничны и существуют
области неопределенности, в которых
условия случая 2 не выполняются.
области решения безграничны и существуют
области неопределенности, в которых
условия случая 2 не выполняются.
Рассмотрим классификацию объекта, заданного вектором х=(4, 3). Подстановка его признаков в выбранные решающие функции дает следующее:
 ;
;
 ;
;
 =>
=>
 ;
;
 ;
;

Поскольку
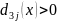 для j=1, 2 и значения функций не попадают
в область неопределенности, то
рассматриваемый образ зачисляется в
класс w3
.
для j=1, 2 и значения функций не попадают
в область неопределенности, то
рассматриваемый образ зачисляется в
класс w3
.

Л
 инейные
разделяющие функции для N классов. 3-й
случай
разделения
Существует
М решающих функций
инейные
разделяющие функции для N классов. 3-й
случай
разделения
Существует
М решающих функций
 таких, что если образ х принадлежит
классу
то
таких, что если образ х принадлежит
классу
то
 для всех j≠i. Эта ситуация является
разновидностью случая 2, т.к. можно
положить
для всех j≠i. Эта ситуация является
разновидностью случая 2, т.к. можно
положить
 Очевидно, что если
для всех j ≠ I, т.е. если классы разделимы,
как в случае 3, то они автоматически
разделимы и как в случае 2.
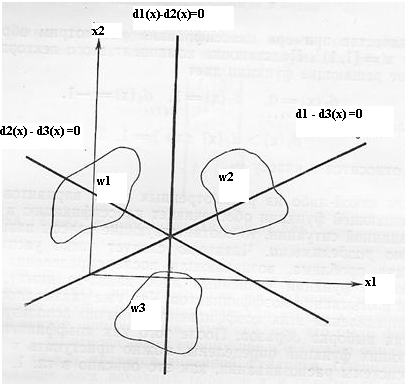
Граница
между классами
и
Очевидно, что если
для всех j ≠ I, т.е. если классы разделимы,
как в случае 3, то они автоматически
разделимы и как в случае 2.
Граница
между классами
и
 определяется теми значениями вектора
х, при которых имеет место равенство
определяется теми значениями вектора
х, при которых имеет место равенство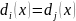 . Поэтому при выводе уравнения разделяющей
границы для классов
и
значения решающих функций
. Поэтому при выводе уравнения разделяющей
границы для классов
и
значения решающих функций
 используются совместно.
Для
образов, принадлежащих классу w1
должны выполняться условия
используются совместно.
Для
образов, принадлежащих классу w1
должны выполняться условия

 В общем случае требуется, чтобы
входящие в класс
образы располагались в положительных
зонах поверхностей
В общем случае требуется, чтобы
входящие в класс
образы располагались в положительных
зонах поверхностей
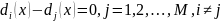 Положительная зона границы
Положительная зона границы
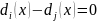 совпадает с отрицательной зоной границы
совпадает с отрицательной зоной границы
 Пример:
Пусть в качестве решающих функций
выбраны следующие:
;
Пример:
Пусть в качестве решающих функций
выбраны следующие:
;
 ;
;
 ;
Разделяющие
границы для трех классов выглядят при
этом так:
;
Разделяющие
границы для трех классов выглядят при
этом так:
 ;
;
 ;
;
 Для того чтобы определить область
решений, соответствующую классу w1
необходимо выделить область, в которой
выполняются неравенства
,
. Эта область совпадает с положительными
зонами для прямых
Для того чтобы определить область
решений, соответствующую классу w1
необходимо выделить область, в которой
выполняются неравенства
,
. Эта область совпадает с положительными
зонами для прямых
 и
и
 .
Область принятия решения о принадлежности
образа классу w2
совпадает с положительными зонами для
прямых
.
Область принятия решения о принадлежности
образа классу w2
совпадает с положительными зонами для
прямых
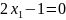 и
и
 .
Область, класса w3
определяется положительными зонами
для прямых
.
Область, класса w3
определяется положительными зонами
для прямых
 и
и
 . В случае 3 (преимущество случая) области
неопределенности как таковые отсутствуют,
за исключением самих разделяющих границ.
. В случае 3 (преимущество случая) области
неопределенности как таковые отсутствуют,
за исключением самих разделяющих границ.
В качестве примера классификации рассмотрим обработку образа х=(1,1). Подстановка признаков образа в выбранные решающие функции дает следующие значения: ;
 ;
;
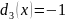 ;
;
Поскольку
 , образ относится к классу w2
Если какой-либо из рассмотренных
вариантов линейной решающей функции
обеспечивает классификацию в некоторой
заданной ситуации, то соответствующие
классы называются линейно
разделимыми.
Основная проблема, возникающая после
определения набора решающих функций,
заключается в отыскании коэффициентов.
Для их определения обычно используется
обучающая выборка образов. После того
как коэффициенты всех решающих функций
определены, можно приступать к построению
системы распознавания.
, образ относится к классу w2
Если какой-либо из рассмотренных
вариантов линейной решающей функции
обеспечивает классификацию в некоторой
заданной ситуации, то соответствующие
классы называются линейно
разделимыми.
Основная проблема, возникающая после
определения набора решающих функций,
заключается в отыскании коэффициентов.
Для их определения обычно используется
обучающая выборка образов. После того
как коэффициенты всех решающих функций
определены, можно приступать к построению
системы распознавания.