1. Распознавание образов. Общие положения.

Цель курса: Принятие решений в условиях неполноты информации.

Задача будет решаться с помощью технических средств. Может быть осуществлено путем моделирования операций, выполняемых живыми организмами в процессе коммуникации и восприятия окружающего мира.

Наиболее удачно положить в основу модели способности человека в распознавании и реакции на окружающую действительность. Сегодня замена человека автоматом жизненно необходима, т.к. зачастую приходится решать задачи в опасных для жизни условиях.

После восприятия информации требуется, чтобы техническое устройство самостоятельно принимало решение на основе анализа им окружающей обстановки. Работа таких роботов становится эффективнее, если они могут адаптироваться к окружающей среде и управлять ситуацией.

Распознавание образов – совокупность методов и средств позволяющих достигнуть, а по возможности и превзойти естественные средства восприятия анализа окружающего мира живыми организмами.

Задачи на основе распознавания образов:

1. Распознавание речи, текстов, изображений

2. Автоматизация медицинской диагностики

3. Область криминалистики

4. Область космоса

5. Синхронный перевод текста

Процедуре распознавания предшествует восприятие информации, а результат распознавания используется для идентификации.

2. Объекты в распознавании образов

Решаемый круг задач относится к образам двух типов.

1. Этот тип образов опирается на реальные объекты, их изображения, или словесные описания

2. К этому типу относятся механизмы формирования понятий, которые могут быть отнесены к области искусственного интеллекта. Сюда входят мнения, пожелания и т.д.

Если рассматривать задачу распознавания в самом общем виде, то ее можно сформулировать как задачу разработки процедуры, позволяющей разбивать множество объектов на классы.

При этом подразумевается, что такое разбиение существует. Подобное утверждение в общем случае не верно, так как если с ним согласиться, то получается, что все и всегда можно формализовать.

Постановка задачи классификации:

Пусть {F} – множество объектов, Х – n-мерное пространство признаков, где Х={x1, x2…xn}. Разбиение на классы можно считать полностью завершенным, если для всех Xi (i=1,2…) выполняется условие: ,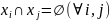

где Xi – совокупность разделения Х и задача заключается в отыскании функции f, которая обеспечивает это разделение, т.е f: X->П(Х).

П(Х) – подмножества Х.

Для решения задачи классификации необходимо найти разделяющую функцию f такую, которая позволит разделить с условием полной сепарабельности (разделимости) все множество объектов на непересекающиеся классы.

Множество С: С={c1, c2 …cp} – совокупность признаков объекта.

Практически используются не все признаки, а лишь те, которые отражают существенные особенности объектов.

Существенные признаки образуют сокращенное множество Y, отличное от множества С: |Y| < =|C| Y={y1, y2… ym}.

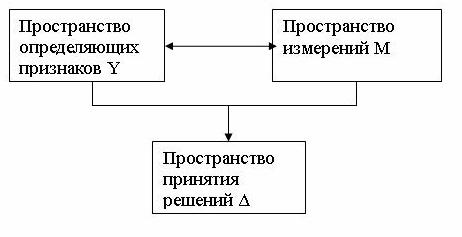
3. Классификация объектов. Понятие расстояния между объектами.

Пример:

{F} – пять треугольников

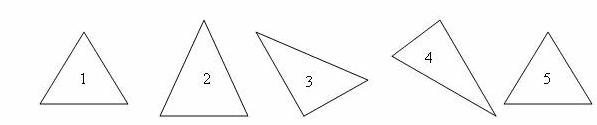
Y={y1, y2, y3} – длины сторон. Измерив длины, получаем М

М1= {2, 2, 2}, М2= {1, 2, 1.5}, М3= {2, 3, 1.5}, М4= {1, 3.5, 4}, М5= {2, 2, 1}.

В результате получаем три класса объектов: С1 – равносторонние треугольники; С2 – равнобедренные треугольники; С3 – остальные треугольники. Расстояние между объектами – средство оценки того, насколько схожи между собой 2 образца, т.е. расстояние, определяет степень сходства образцов.

Для определения этого понятия было предложено множество математических выражений. Это связано со многими причинами: спецификой решаемых задач, используемыми техническими средствами.

Уточним это понятие для случая метрического пространства Х. Будем называть расстоянием между точкой 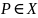и классом 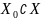величину d1, определяемую выражением

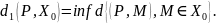
inf = min;

Расстояние между 2-мя классам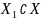и и 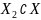определяется величиной d2

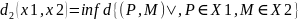
d1 – Евклидово расстояние,

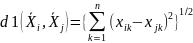
d2 – расстояние по Манхэттену,

d3 – Чебышевское расстояние,

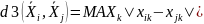
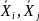– векторы, между которыми оценивается расстояние, 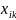– к-ая составляющая вектора Хi.