Базові операції обробки матриць

Однотипну обробку всіх елементів матриці найлегше здійснити шляхом її обходу за рядками або стовпцями. Методом реалізації такого обходу є використання вкладених циклів for. При цьому, як правило, індекси елементів масиву використовуються як параметри відповідних циклів.

Перелік базових операцій над матрицями та їх елементами:

1. введення-виведення матриці, її ініціалізація;

2. створення нової матриці за заданим алгоритмом;

3. пошук елементів матриці за певним критерієм;

4. визначення, чи задовольняє матриця або окремі її елементи певній властивості;

5. виконання певних операцій над компонентами матриць (переставлення рядків і стовпців, множення матриць тощо).

Введення-виведення матриці здійснюється аналогічно введенню-виведенню одновимірних масивів. Наприклад,

for (int i=0; i<n; i++) //зовнішній цикл по рядках

for (int j=0; j< n; j++) //внутрішній цикл по стовпцях

cin>>a[i][j] // введення елемента з клавіатури

Пошук максимального або мінімального елемента матриці принципово не відрізняється від розв’язання аналогічної задачі для одновимірних масивів.

Перестановка або обмін значеннями між двома елементами матриці здійснюється аналогічно до обміну значеннями між двома змінними. Часто цю операцію поширюють на цілий рядок або стовпець (рис. 5), використовуючи для цього арифметичний цикл for.

Рис. 5. Перестановка рядків матриці

Вставка та видалення окремих елементів матриці є некоректними операціями, оскільки приводять до невизначеності щодо поведінки інших елементів. Тому найчастіше під час перетворення матриць вставку або видалення поширюють на цілий рядок або стовпець (рис. 6, 7).

Рис. 6. Вставка рядка у матрицю

Рис. 7. Видалення рядка із матриці

Транспонування матриці – обмін місцями її рядків і стовпців. Передбачає використання допоміжної матриці.

Операція множення матриць A і B (AB) передбачає, що кожен елемент результуючої матриці обчислюється наступним чином:

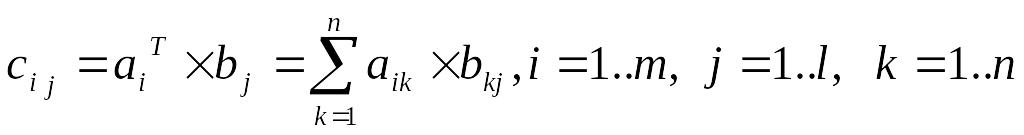
Вона визначена тільки тоді, коли кількість стовпців матриці A дорівнює кількості рядків матриці B.

Множення двох матриць можна зобразити схемою:

Тут A — (m  n)-матриця; B — (n  l)-матриця; a_i^T— i-й вектор-рядок матриці А; b_j — j-й вектор-стовпець матриці B.

Базові операції обробки матриць слід реалізовувати у вигляді функцій, які надалі можуть бути використані як «архітектурні блоки» при побудові складних програм.

Приклад. Видалення вказаного рядка матриці.

#include <iostream.h>

#include <stdlib.h>

#include <time.h>

#include <iomanip.h>

using namespace std;

typedef int Matrix[10][10]; //тип матриці

Matrix А; //вихідна матриця

int n,m; //кількість рядків і стовпчиків матриці

void input(); //генерація матриці

void output(); //виведення матриці

void delete_row(int); //видалення рядка матриці

//=============== головна функцiя ================

int main()

{ int k; //номер рядка, що видаляється

cout<<"Input n,m: "; cin>>n>>m; //ввести розмірність матриці

input(); //генерувати матрицю

output(); //вивести згенеровану матрицю

cout<<"Input number of row:"; cin>>k; //ввести номер рядка, що видаляється

delete_row(k); //видалити вказаний рядок

output(); //вивести отриману матрицю

system("pause");

}

//============== генерація матриці =================

void input()

{ srand(time(NULL));

for (int i=0; i<n; i++)

for (int j=0; j<m; j++)

a[i][j] = rand()%20; //генерація поточного елемента матриці

}

//=============== виведення матриці =================

void output()

{ for (int i=0; i<n; i++)

{ for (int j=0; j<m; j++)

cout<<setw(4)<< a[i][j]; //виведення елементів рядка

cout<<endl; //перехід на новий рядок

}

}

//======== видалення вказаного рядка матриці ========

void delete_row(int k1)

{ for (int i=k1-1; i<n-1; i++) //перегляд рядків, які будуть зсуватися

for (int j=0; j<m; j++)

a[i][j] = a[i+1][j]; //зсув рядка

n--; //зменшення загальної кількості рядків

}