Ферромагнетизм

Магнетизм ферромагнетиков определяется не магнитным моментом, связанным с орбитальным движением электронов, а с собственным магнитным моментом электронов.

С ила Ампера, действующая на кольцо: .

.

Опыт Штерна и Гермаха показал, что ориентация спина относительно выбранного направления может принимать только дискретные значения.

В ферромагнетиках электроны в силу т.н. «обменного воздействия» выстраиваются таким образом, чтобы их спины были направлены в одну сторону.

Области, в которых направлен в одну сторону, называются доменами.

Для ферромагнетиков:

О тношение относится только к начальной кривой. – остаточное поле, – коэцитивная сила. Сам график называется петлёй гистерезиса.

.

При повышении температуры ферромагнетика его свойства внезапно исчезают. Температура, при которой это происходит, называется точкой Кюри.

При температуре выше, чем точка Кюри, ферромагнетик превращается в парамагнетик и (для ферромагнетика , где – точка Кюри).

Работа, совершаемая при перемещении тока в магнитном поле

Сила Ампера . Работа её .

В приведённом контуре сила, действующая на подвижный стержень (справа) ( – изменение площади). Поток вектора магнитной индукции . Если , то . Т.к. , то и, т.к. , то .

В случае произвольного контура при элементарном перемещении какого-нибудь его элемента . Для всего контура . При полном перемещении из положения 1 в положение 2 . При .

Работа производится за счёт источника тока, который при изменении контура поддерживает в нём постоянный ток.

Явление электромагнитной индукции

В замкнутом проводящем контуре при изменении потока магнитной индукции через поверхность, ограниченную этим контуром, возникает электрический ток. ЭДС этого контура .

Индукционный ток всегда направлен так, чтобы противодействовать причине, его вызывающей (правило Ленца).

Сила, действующая на левый контур , т.е. , следовательно, ток в контурах течёт в разных направлениях.

С ила Лоренца, действующая на электроны в стержне в контуре, . Напряженность поля в ней, возникающая при этом, . ЭДС индукции .

Рассмотрим кусок стержня, соединяющего точки 1 и 2:

. Отсюда видно, что электрический ток и его работу производит .

Для соленоида , где – потокосцепление. Если поток через все витки одинаков, то , где N – число витков.

Явление самоиндукции

Закон Био-Савара говорит о том, что , где – вектор магнитной индукции, I – сила тока, текущего через элементарный участок , – радиус-вектор точки, в который определяется вектор магнитной индукции относительно этого участка. Из этой формулы видно, что , следовательно, и .

Величина называется индуктивностью контура.

Индуктивность контура зависит от формы и размеров контура, а для ферромагнетиков и от силы тока, текущего через него.

ЭДС самоиндукции . При постоянном L .

Ток при замыкании и размыкании цепи с индуктивностью:

Пусть в контуре течёт ток , где – ЭДС источника тока, R – сопротивление контура. При выключении источника тока возникает ЭДС самоиндукции . При включении источника тока .

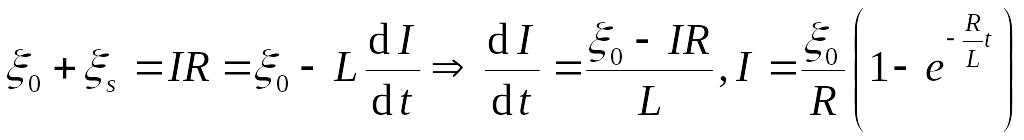Взаимная индуктивность:

Пусть есть две рамки с током, центры которых находятся на одной прямой, перпендикулярной плоскостям рамок. Тогда при включении или выключении тока в обеих рамках в них возбуждается ЭДС индукции: .

Если магнитный поток одного из контуров пронизывает другой контур, то такие контуры называются связанными.

Теорема взаимности: Если в окружающем пространстве отсутствуют ферромагнетики, то .

Коэффициенты и называются взаимной индуктивностью.

Работа, совершаемая ЭДС индукции за время , – работа сторонних сил: , где Q – выделение джоулева тепла, – энергия магнитного поля, . Если одновременно включить обе рамки, то , следовательно, энергия магнитного поля – величина не аддитивная, т.е. энергия каждого контура, при сближении их, будет не равна сумме каждого контура.

Рассмотрим длинный соленоид:

Индукция внутри него , где n – количество витков на единицу длины, потокосцепление . Поток через один виток , где S – площадь поперечного сечения соленоида. , где l – длина, а V – объём соленоида, следовательно, , напряжённость магнитного поля внутри соленоида , т.е. и .

Плотность энергии внутри соленоида .

Р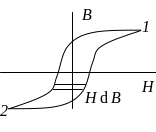 абота по перемагничиванию ферромагнетика

.

При переходе вся энергия уходит на перестраивание доменов, т.е. на тепло. Работа над единицей объёма площади петли гистерезиса.

Вихревое электрическое поле

При перемещении контура в неоднородном магнитном поле в нём возникает напряжённость электрического поля : . Напряжённость внутри контура , где – обычное поле статических зарядов. .

Ток смещения

, где – плотность тока проводимости, , где  – плотность зарядов. В стационарном поле и , следовательно, линии тока проводимости замкнуты. . Максвелл предложил к первому уравнению добавить .

Отсюда следует, что . Одно из решений этого уравнения: , следовательно, .

Р ассмотрим контур с конденсатором. Ток, текущий через контур, представляющий собой кольцо, перпендикулярное проводу, ведущему к конденсатору, , где S – поверхность этого контура. Если провести эту поверхность через внутренность конденсатора так, как показано на рисунке, то получится, что ток через неё не течёт, следовательно, и , где q – сторонний заряд.

Уравнения Максвелла

– уравнения Максвелла в дифференциальной форме.

– уравнения Максвелла в интегральной форме.

Эти уравнения релятивистски инварианты. Краевые условия: . Материальные уравнения: , где  – проводимость, , где r – удельное сопротивление. Уравнение непрерывности: .

Электромагнитные волны

Рассмотрим волны в среде непроводящей, незаряженной и однородной. . Тогда уравнения Максвелла будут выглядеть так: . Возьмём в первом уравнении ротор от правой и левой части: . При этом – волновое уравнение. Скорость распространения волны . Точно так же . Величина – электродинамическая постоянная. Скорость волны, таким образом, . В вакууме и , следовательно, м/с – скорость света.

Плоские электромагнитные волны

Волна называется плоской, если в любой момент времени в любой точке плоскости, перпендикулярной направлению распространения волны векторы поля имеют одинаковое значение. Т.е., если волна распространяется вдоль оси x, то векторы электрической и магнитной напряжённости зависит только от координаты x, и не зависят от координат y и z.

Уравнения Максвелла в этом случае преобразуются следующим образом: , так как напряжённость электрического поля не зависит от координат y и z, , . Отсюда следует, что электромагнитная волна по природе своей поперечна, т.е. изменяющиеся величины находятся в плоскости, перпендикулярной направлению распространения волны.

Окончательный результат: .

Выберем такую систему координат, что и . Решение волнового уравнения: . Подставим их: Аналогично и вектор напряжённости магнитного поля; . Окончательно, .

Энергия электромагнитного поля

Плотность потока энергии , где w – плотность энергии, – скорость волны – энергия, переносимая волной через единичное сечение в единицу времени. В случае электромагнитной волны – вектор Пойнтинга.

Поток энергии , где – элемент поверхности.

Импульс электромагнитного поля

Пусть на поверхность попадает волна. Под действием образуется ток плотностью . Благодаря на этот ток действует силы Лоренца . Импульс этой силы . Выделение энергии , где (скорости волны).

Движение заряженных частиц в электромагнитных полях

Однородное поле: заряд , индукция , скорость . Отсюда видно, что сила Лоренца всегда перпендикулярна скорости, следовательно, заряд будет двигаться по окружности. – удельный заряд. Период вращения . Если , то , следовательно, заряд будет двигаться по спирали вдоль вектора с шагом .

Электрические колебания

1. Свободные незатухающие колебания: – время распространения электромагнитного возмущения. Здесь l – длина провода, с – скорость света. Будем рассматривать такие проводники, для которых это время очень мало. Тогда силу тока на всей длине проводника можно считать одинаковой. Такие токи называется квазистационарными.

Н апишем уравнение Кирхгофа для этого контура: . При этом , где L – индуктивность катушки, C – ёмкость конденсатора. Таким образом, . Введём обозначение: . Тогда это уравнение запишется в виде: . Вещественным решением этого уравнения является функция , где – максимальный заряд на конденсаторе. Отсюда следует, что период колебаний – формула Томпсона. Напряжение на обкладках конденсатора .

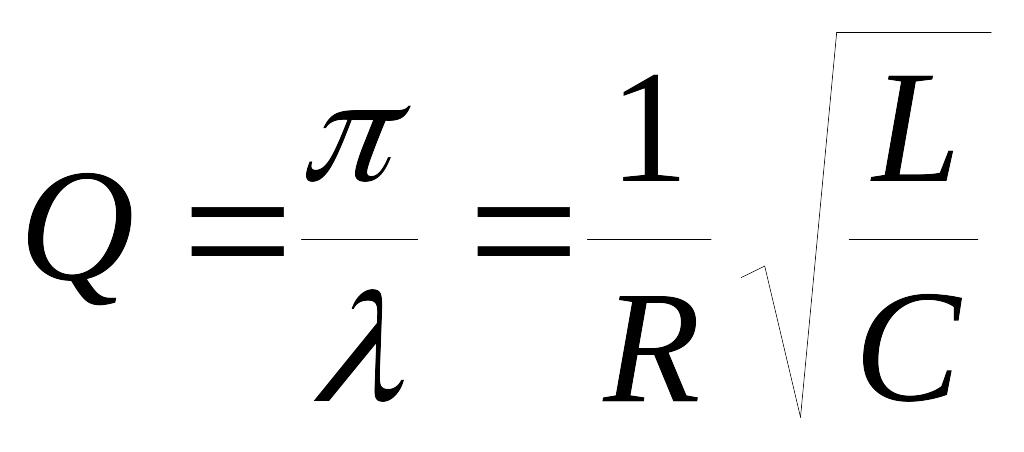2. Свободные затухающие колебания: в этом случае уравнение Кирхгофа примет вид: . Обозначим, как и раньше, , а . Тогда это уравнение запишется так: . Решением этого уравнения является функция . Напряжение на обкладках конденсатора . Ток в контуре Логарифмический декремент затухания: . Добротность . При процесс становится апериодическим. Сопротивление – критическое.

3. Вынужденные электрические колебания:

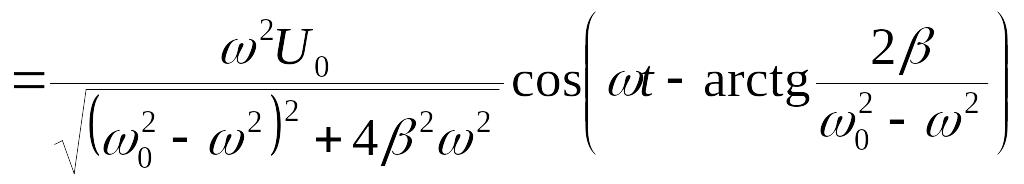Подадим напряжение . Уравнение Кирхгофа для этого контура: . Произведя аналогичные замены, получим: . Решением этого уравнения является функция: . Сила тока в контуре . Напряжение в катушке . Напряжение на обкладках конденсатора .

Для заряда резонансная частота .