Вектор (электрическое смещение).

И з теоремы Гаусса для вектора напряжённости следует, что , где – связанный заряд. . Введём . Тогда и . В то же время . Тогда , где .  – диэлектрическая проницаемость диэлектрика.

Ц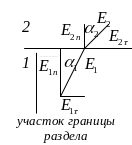 иркуляция вдоль этого контура равна 0, следовательно, . Уменьшая высоту контура до 0, получим: и и . Рассмотрим нормальную составляющую для так же как и для . Тогда , где  – плотность заряда на границе раздела. В случае отсутствия стороннего заряда на границе раздела .

– закон преломления для силовых линий поля на границе раздела двух диэлектриков.

Пусть среда 2 – проводник. Тогда и и .

и . Плотность связанного заряда на границе диэлектрика и проводника .

Если однородный изотропный диэлектрик полностью заполняет собой пространство между эквипотенциальными поверхностями, то напряжённость поля в диэлектрике в  раз меньше, чем если бы она была в этой точке поля в отсутствие диэлектрика:

.

Энергия системы зарядов.

Поместим заряд в любую точку пространства. После этого поместим заряд на расстоянии от . При этом будет совершена работа . Поместим заряд на расстоянии от и от . Тогда работа , и полная работа . В общем виде , следовательно, энергия электрических зарядов , где – потенциал, создаваемые всеми зарядами, кроме i-го. В случае непрерывного заряда . Для проводника , где q – полный заряд проводника, а  – его потенциал. Т.к. ёмкость проводника , то . Для диэлектрика, заключённого между пластинами конденсатора, . Выразим энергию через напряжённость поля: . Объёмная плотность энергии – энергия, которой обладает поле в отсутствие диэлектрика, а – работа, затраченная на поляризацию диэлектрика.

, где – смещение из положения равновесия. . При этом .

Пусть есть пространство с полем напряжённостью . Добавив несколько зарядов, мы получим пространство напряжённостью . Плотность энергии в этом пространстве , где и его энергия . Но , следовательно, . Отсюда видно, что энергия не обладает свойством аддитивности. Взаимная энергия определяется взаимным расположением зарядов.

Постоянный электрический ток

Направление вектора плотности тока совпадает с направлением движения заряда, а его модуль , что отражает закон сохранения заряда. Уравнение непрерывности: . Для постоянного тока .

Возьмём маленький кусочек проводника площадью S и длиной . Тогда его сопротивление , ток и, т.к. , то – закон Ома в дифференциальной форме.

Для того, чтобы в проводнике существовал электрический ток, в нём помимо электростатических сил должны действовать силы другой природы, которые переносили бы заряд в сторону возрастания потенциала (сторонние силы).

– напряжённость поля сторонних сил, . Тогда работа сторонних сил – электродвижущая сила.

Напряжение на данном участке – это работа, которую силы, электростатические и сторонние, действующие на данном участке, производят при перемещении единичного положительного заряда.

Участок цепи, на котором действует ЭДС, называется неоднородным.

На этом участке – обобщённый закон Ома в дифференциальной форме.

Для провода , но , следовательно, .

Разрядка конденсатора:

Рассмотрим закон убывания заряда для конденсатора ёмкости C при его разрядке через сеть с сопротивлением R: . Т.к. при , то .

Зарядка конденсатора:

З акон Ома для неоднородного участка цепи: , где U – напряжение на конденсаторе. . Обозначим . Тогда . Т.к. при , то . Здесь – максимальный заряд, который может быть накоплен на конденсаторе. Напряжение на обкладках .