
- •III семестр
- •Электростатика
- •Теорема Гаусса
- •Уравнение Пуассона
- •Диэлектрики
- •Вектор (электрическое смещение).
- •Энергия системы зарядов.
- •Постоянный электрический ток
- •Магнитное поле в вакууме
- •Сила Ампера
- •Контур с током в однородном магнитном поле.
- •Магнитное поле в веществе
- •Ферромагнетизм
- •Явление электромагнитной индукции
- •Явление самоиндукции
III семестр
Электростатика
Заряд – это физическая величина, являющаяся источником электрического поля.
Заряды бывают двух типов: «+» и «–». Количество зарядов того и другого типа во Вселенной, скорее всего, одинаково.
Закон сохранения заряда: в замкнутой системе количество заряда сохраняется.
Электрический заряд – релятивистски
инвариантная величина. Заряд дискретен.
Минимальное количество заряда
![]() Кл. Кл=А/с.
Кл. Кл=А/с.
Закон Кулона: Сила взаимодействия
двух точечных неподвижных зарядов прямо
пропорциональна величине этих зарядов
и обратно пропорциональна квадрату
расстояния между ними:
 .
. Здесь
Здесь
![]() ,
где
,
где
![]() Ф/м. В случае нескольких тел
Ф/м. В случае нескольких тел
![]() .
.
Для обнаружения электрического поля необходимо внести в него пробный заряд.
Напряжённость электрического поля
![]() (
(![]() – пробный заряд
– пробный заряд
![]() ).
В случае нескольких зарядов
).
В случае нескольких зарядов
![]() – принцип суперпозиции (напряжённость
электростатического поля, создаваемого
системой из N зарядов,
равняется векторной сумме напряжённостей
полей, создаваемых каждым зарядом в
отдельности.
– принцип суперпозиции (напряжённость
электростатического поля, создаваемого
системой из N зарядов,
равняется векторной сумме напряжённостей
полей, создаваемых каждым зарядом в
отдельности.
 .
. В случае непрерывного распределения
заряда
В случае непрерывного распределения
заряда
 .
.
Силовые линии – это линии, проведённые таким образом, чтобы касательная к этим линиям в любой точке пространства совпадала с вектором напряжённости.
В случае положительного заряда линии поля выходят из заряда, в случае отрицательного – входят в заряд. Силовая линия не может быть замкнутой и должна начинаться на положительном заряде или в бесконечности и кончаться на отрицательном или в бесконечности, причём она не может начинаться и кончаться в бесконечности.
Область пространства, каждой точке которого сопоставлен вектор, называется векторным полем (скаляр – скалярным полем).
Пусть какой-то заряд в электрическом поле, создаваемом зарядом q перешёл из точки 1 в точку 2:
Р абота,
которая при этом совершится не зависит
от траектории:
абота,
которая при этом совершится не зависит
от траектории:
 ,
,
![]() ,
где
,
где
![]() – единичный вектор,
– пробный заряд.
– единичный вектор,
– пробный заряд.
 .
.
 .
В то же время
.
В то же время
![]() (
(![]() – потенциальная энергия). Тогда
– потенциальная энергия). Тогда
![]() .
Обычно const определяют
таким образом, чтобы при
.
Обычно const определяют
таким образом, чтобы при
![]() ,
т.е.
,
т.е.
![]() и
и
![]() .
.
Потенциал
![]() .
Численно потенциал равен работе, которую
совершают силы электростатического
поля при переносе положительного
электрического заряда из одной точки
поля на бесконечность:
.
Численно потенциал равен работе, которую
совершают силы электростатического
поля при переносе положительного
электрического заряда из одной точки
поля на бесконечность:
![]() ,
где
,
где
![]() – потенциал i-й точки
в поле заряда q.
– потенциал i-й точки
в поле заряда q.
![]() .
.
В случае нескольких зарядов
 .
Тогда
.
Тогда
![]() и
и
![]() .
.
Потенциал измеряется в вольтах. Вольт – это потенциал такой точки поля, для перенесения в которую заряда в 1 Кл требуется совершить работу в 1 Дж.
Так как
![]() и
и
![]() ,
то
,
то
![]() и
и
![]() .
.
 и в то же время
и в то же время
![]() ,
значит,
,
значит,
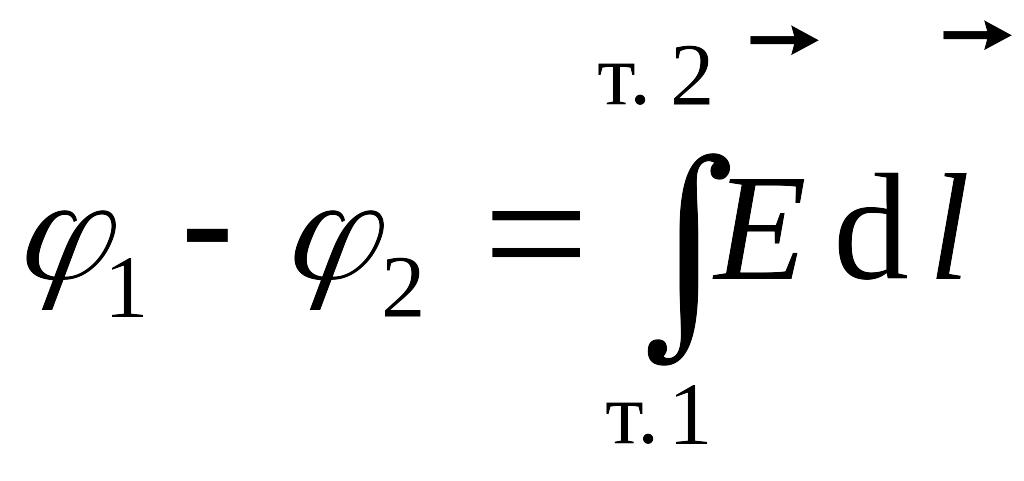 .
.
Поверхности в поле, для
которых
![]() называются эквипотенциальными.
называются эквипотенциальными.
Так как при перемещении заряда по
эквипотенциальной поверхности
 ,
то
,
то
![]() .
.
Теорема Гаусса
Часть пространства,
ограниченная конической поверхностью,
опирающейся на замкнутую кривую
называется телесным углом. Величиной
телесного угла с вершиной в точке O
называется отношение площади, вырезаемой
этим углом на поверхности сферы к
квадрату радиуса:
![]() .
Телесный угол измеряется в стерадианах.
Телесный угол полной сферы –
.
Телесный угол измеряется в стерадианах.
Телесный угол полной сферы –
![]() стерадиан.
стерадиан.
П усть
есть векторное поле произвольного
усть
есть векторное поле произвольного
![]() .
В этом векторном поле выберем площадку
.
В этом векторном поле выберем площадку
![]() .
Восстановим к ней нормаль и выберем
одну из них как положительную.
.
Восстановим к ней нормаль и выберем
одну из них как положительную.
Т огда
величина
огда
величина
![]() – поток вектора
через
– поток вектора
через
![]() .
.
![]()
![]() .
В случае поверхности
.
В случае поверхности
![]() .
Найдём поток
.
Найдём поток
![]() через
через
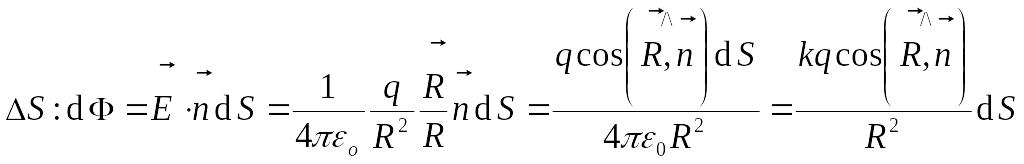 .
Телесный угол
.
Телесный угол
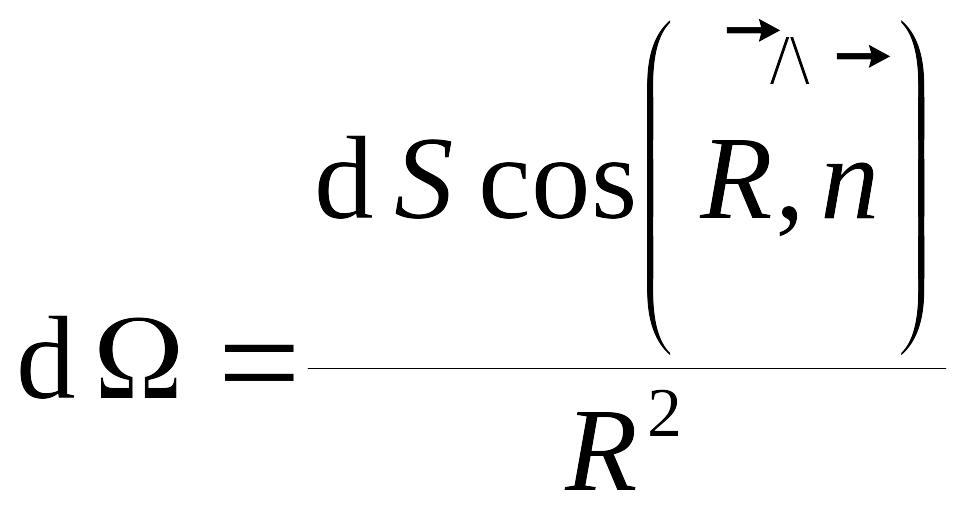
![]() .
В случае замкнутой поверхности, окружающей
заряд,
.
В случае замкнутой поверхности, окружающей
заряд,
![]() .
Если заряд вне поверхности, то
.
Если заряд вне поверхности, то
![]() ,
т.к. в половине площади поверхности
нормаль направлена к заряду, и в половине
– от заряда.
,
т.к. в половине площади поверхности
нормаль направлена к заряду, и в половине
– от заряда.
Таким образом,
![]() .
Т.к. в случае нескольких зарядов
.
Т.к. в случае нескольких зарядов
![]() ,
то
,
то
 .
.
Теорема Гаусса: В
произвольном электростатическом поле
в вакууме поток
через произвольную замкнутую поверхность
равен суммарному заряду, находящемуся
в этой поверхности, делённому на
![]() .
.
Теорему Гаусса удобно применять, когда известно направление в каждой точке пространства, и когда оно обладает определённой симметрией, которая позволяет нам выбрать такую поверхность интегрирования, в каждой точке которой E постоянно и направление составляет один и тот же угол с направлением нормали к поверхности.
Четыре типовые задачи, в которых удобно применять теорему Гаусса для нахождения напряжённости электрического поля на расстоянии x от объекта:
Бесконечная равномерно заряженная плоскость с плотностью заряда .
![]() .
.
2. Бесконечный равномерно заряженный цилиндр с плотностью заряда .
![]()
 .
.
3. Сфера зарядом q и радиусом R.
Если
![]() ,
то
,
то
![]() .
Если же
.
Если же
![]() ,
то
,
то
![]() ,
следовательно, поле снаружи сферы
совпадает с полем точечного заряда той
же величины.
,
следовательно, поле снаружи сферы
совпадает с полем точечного заряда той
же величины.
4. Шар зарядом q и радиусом R.
![]() ,
где – объёмная
плотность заряда,
,
где – объёмная
плотность заряда,
![]() .
Если
,
то
.
Если
,
то
![]() .
Если
,
то
.
Если
,
то
![]() .
.
Если есть поле
,
то дивергенция
 ,
где V
– объём, окружённый поверхностью.
,
где V
– объём, окружённый поверхностью.
![]() .
. Здесь
Здесь
![]() – проекция
на нормаль
– проекция
на нормаль
![]() ,
,
![]() – приращение потока
за счёт проекции его на ось x.
Аналогично
– приращение потока
за счёт проекции его на ось x.
Аналогично
![]() .
При
.
При
![]() приближённое равенство переходит в
равенство и
приближённое равенство переходит в
равенство и
![]() .
.
Теорема Остроградского-Гаусса:
![]() .
.
Следует из того, что
![]() .
.
Тогда
![]() ,
где – объёмная
плотность заряда. Отсюда следует, что
,
где – объёмная
плотность заряда. Отсюда следует, что
![]() (т.к. S – произвольная
поверхность) – теорема Гаусса в
дифференциальной форме.
(т.к. S – произвольная
поверхность) – теорема Гаусса в
дифференциальной форме.
Циркуляцией
называется
![]() ,
где Г – контур,
,
где Г – контур,
![]() – элемент контура).
– элемент контура).
Теорема о циркуляции
:
![]() .
.
Следует из того, что
![]() ,
т.к. работа совершается по замкнутому
контуру.
,
т.к. работа совершается по замкнутому
контуру.
Диполь
Диполь – это система из двух точечных зарядов, равных по величине, противоположного знака, находящиеся на расстоянии друг от друга маленьком по отношению к той точке, где требуется найти поле этой системы.
Прямая, проходящая через оба заряда, называется осью диполя.
![]() .
. Потенциал в рассматриваемой точке
Потенциал в рассматриваемой точке
![]() ,
т.к.
,
т.к.
![]() .
.
![]() ,
где
– орт
,
где
– орт
![]() ,
а
,
а
![]() – дипольный момент.
– дипольный момент.
В декартовой системе координат
![]() .
Найдем выражение для
.
Найдем выражение для
![]() в полярной системе координат:
в полярной системе координат:
![]() .
При этом
.
При этом
![]() и
и
![]() ,
следовательно,
,
следовательно,

 .
Найдём выражение для напряжённости
поля:
.
Найдём выражение для напряжённости
поля:
 и
и
![]() .
Компонента
.
Компонента

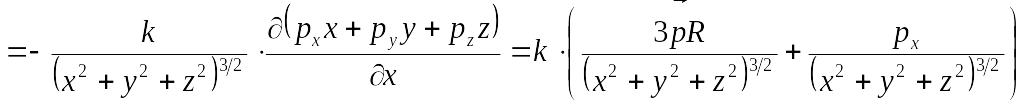 .
Для других двух компонент – аналогично.
Отсюда
.
Для других двух компонент – аналогично.
Отсюда
 .
.
Мультидипольное разложение
Пусть система зарядов сосредоточена в
начале координат так, что каждый заряд
характеризуется вектором
![]() .
Найдём потенциал такой системы на
расстоянии, характеризующемся
радиус-вектором
.
Найдём потенциал такой системы на
расстоянии, характеризующемся
радиус-вектором
![]() и углом
и углом
 .
При этом
.
При этом
 .
Из формулы Тейлора можно получить, что
при
.
Из формулы Тейлора можно получить, что
при
![]() будет
будет
![]()
![]() Тогда
Тогда
 и
и
 .
Если эта сумма равна 0, то следует
использовать также и третий член в
формуле Тейлора, и если сумма опять
равна 0, то четвёртый и т.д.
.
Если эта сумма равна 0, то следует
использовать также и третий член в
формуле Тейлора, и если сумма опять
равна 0, то четвёртый и т.д.
![]() – дипольный момент системы.
– дипольный момент системы.
Тогда
 .
.
Диполь в электрическом поле
М омент,
действующий на диполь в однородном поле
омент,
действующий на диполь в однородном поле
![]()
![]() .
.
С ила,
действующая на диполь в неоднородном
поле:
ила,
действующая на диполь в неоднородном
поле:
![]()
В случае, если неоднородное поле
симметрично относительно оси x,
то сила
![]() ,
где – угол
наклона диполя к оси; его энергия
,
где – угол
наклона диполя к оси; его энергия
![]() .
.
Проводники
Проводники – это такие тела, которые содержат много свободных электронов, т.е. электронов, которые могут двигаться по проводнику в любую сторону, но не могут покинуть его поверхность.
Под действием электрического поля за короткое время получается равновесное распределение зарядов на проводнике.
Условия равновесного распределения: напряжённость поля внутри проводника равна 0, а на поверхности проводника перпендикулярна ей в любой точке.
Напряжённость электрического поля внутри проводника равна 0, следовательно, потенциал проводника постоянен всюду в проводнике, а его поверхность является эквипотенциальной поверхностью.
П оток
вектора напряжённости через цилиндр,
взятый на проводнике так, как показано
на рисунке,
оток
вектора напряжённости через цилиндр,
взятый на проводнике так, как показано
на рисунке,
![]() ,
так как напряжённость поля внутри
проводника равна 0. По теореме Гаусса
,
так как напряжённость поля внутри
проводника равна 0. По теореме Гаусса
![]() .
Если сообщить проводнику какой-то заряд,
то через короткий промежуток времени
он весь выйдёт на поверхность, и в
результате на неё будет действовать
растягивающая сила:
.
Если сообщить проводнику какой-то заряд,
то через короткий промежуток времени
он весь выйдёт на поверхность, и в
результате на неё будет действовать
растягивающая сила:
![]() ,
где
,
где
![]() – поля, создающееся зарядом, не находящимся
на площадке
.
Заряд, который находится на площадке
,
создаёт поле
– поля, создающееся зарядом, не находящимся
на площадке
.
Заряд, который находится на площадке
,
создаёт поле
![]() ,
направленное в обе стороны от площадки:
,
направленное в обе стороны от площадки:

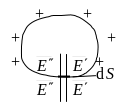 и
и
![]() ,
где
,
где
![]() – нормаль к площадке.
– нормаль к площадке.
